Why does this phenomenon occur?

As children we often yearned for explanations of the world around us, pestering our parents and teachers with simple but baffling questions. I bet you have asked many of them yourself.

Why is the sky blue?

Why is the sea salty?

Why is it cold in the winter?

This childish curiosity is plays an enormous role in scientific practice. The questions are also all similar, not only because we persistently ask them as children, but because they are all of the form, "Why does this phenomenon occur?"

Such questions demand a special kind of answer, which is often called an an explanation. Not just any answer will do. And an appropriate answer is often tricky enough to baffle one's parents.

For example, to explain why the sky is blue, one has to start with a phenomenon known as Rayleigh scattering. When light waves crash into the molecules of the Earth's atmosphere, the long waves tend to pass through with very little deflection, while the short ones get dramatically deflected this way and that by the molecules of air — and the short wavelengths are blue.

Since the short blue light waves bounce off in all directions when they hit the atmosphere, you can be sure to get hit by blue light from the sky no matter where you're standing.

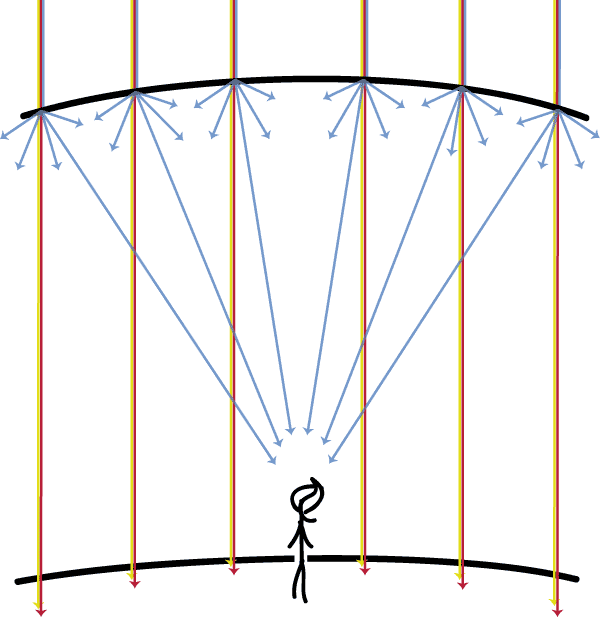
In fact, a mixture of both blue and violet both scatter and hit your eyes, which to some animals might make the sky look blue-violet. However, the cone photoreceptors in the human eye, which are responsible for colour vision, turn out (scientific paper here) to react to a pure blue-violet signal as if it were a combination of blue and white light. This why the sky appears to humans as a "sky blue" colour instead of blue-violet.

Our aim today is to try to understand what is required of an adequate answer to questions of the form, "Why does the phenomenon occur?" That is, we would like to understand the nature of a scientific explanation. Sometimes you know it when you see it. But sometimes it is not so obvious.

We will be four different takes on what a scientific explanation amounts to. Each one tells us something about the nature of scientific explanation. But perhaps none quite hit the nail on the head.

We will then look at a simple application of the theory of scientific explanations, to the question of anthropic explanations.

The DN Model

Overview

Here is a simple example of the DN model in action. You may remember from some of our earlier discussions that Kepler discovered that planets travel in ellipses around the sun. This is known as Kepler's First Law. But suppose someone were to ask, Why do the planets travel in ellipses? Why does this phenomenon occur?

A convincing explanation of this phenomenon of this famously given by Sir Isaac Newton in his magnum opus, Principia Mathematica. Newton began by assuming the following things.

1. Three laws of motion, together with inverse-square law of gravitation.
2. Further premises that the sun is approximately fixed in place, and a planet begins with some initial velocity perpendicular to the direction of the sun.

From these assumptions, Newton was able to derive Kepler's first law, and indeed all of Kepler's laws. That is, Newton deduced the phenomenon from the laws and some plausible initial conditions. This remarkable achievement remains a paradigmatic example of a scientific explanation. It is also the central inspiration for the DN-model of explanation.

The DN model is the proposal that explanations have the structure of sound deductive arguments with a law of nature as an essential premise. We have seen already (see Lecture 8) that there is little agreement as to what a law of nature is. But let us understand a "law" in any plausible way. According to the DN account, a law looks like the following.

If a phenomenon can be deduced from a law (which must play a necessary role in the derivation), together with some further assumptions, then this deduction is called a DN-explanation of the phenomenon.

(N.B. The name "DN" was given to this model by the philosopher Carl Hempel, who used it to stand for the "Deducto-Nomological" Model. "Deducto" is short for deduction, while "Nomological" refers to a law-like principle. He also referred to the phenomenon to be explained the explanandum, and the premises that explain it as the explanans. I myself do not find this terminology helpful, but mention here to flag the fact that it is often used by philosophers.)

The DN account is designed with deterministic laws in mind. (Hempel proposed an alternative for statistical laws, which we will not discuss here.) He also intended it to apply to both general regularities like Kepler's laws, as well as particular events such as the impact of a meteor.

Finally, it was originally proposed that all and only scientific explanations conform to the DN model of explanation. Although the DN model had great success in describing a number of explanations in the history of science, this assumption turned out to be particularly questionable.

Problems with the DN Model

The DN model has the honour of being one of the first attempts to systematically characterise the nature of scientific explanation. It is also one of the most naïve, and falls prey to a number of famous counterexamples. Much of the recent work on scientific explanations has gone toward overcoming these examples.

Problem 1: The Flagpole

Let's begin with something that looks like a good explanation. Suppose someone sees a flagpole at a certain time of day and asks, "Why does the shadow of the flagpole have this length?" You are charged with explaining this phenomenon, and so you argue as follows.

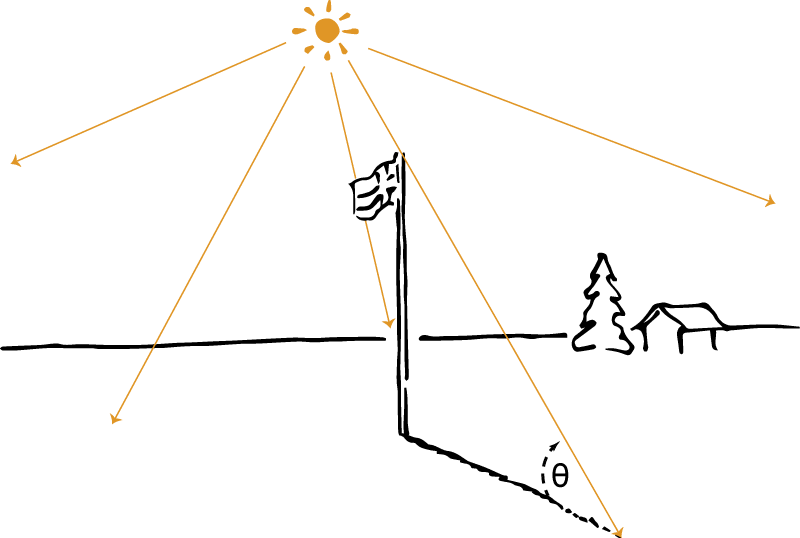
1. Lawlike statement. Light from the sun propagates along straight (Euclidean) lines.
2. Further premises. The flag pole has height H, and the light from the sun makes an angle θ with the flagpole.
3. Therefore: Phenomenon. Therefore, the length of the shadow is L = H/tanθ.

That does provide a good explanation of the length of the shadow. Here the DN model succeeds.

But now suppose instead that somebody asks under the same circumstances, "Why does the flagpole have that length?" What would your intuitive explanation be?

Mine would be that conforms to the government's Guide to Flying Flags, or that the client ordered it that way from the manufacturer, or that the flag needed to be raised just higher than the barnyard.

But according to the DN model, the following just as well counts as an explanation.

1. Lawlike statement. Light from the sun propagates along straight (Euclidean) lines.
2. Further premises. The shadow has length L, and the light from the sun makes an angle θ with the flagpole.
3. Phenomenon. Therefore, the height of the flagpole is H = Ltanθ.

But although this "explanation" is of exactly the same form as the previous one, and indeed an equally sound deduction, it is also not an explanation of the kind that one would normally thing establishes why a flagpole has a certain length.

Clearly, something has gone wrong with the DN model of explanation.

Problem 2: The Birth Control Pills

To drive the difficulties with the DN model, here is another famous problem begins with a character that we will call Joe, was born male, but decides one day to go on birth control pills.

Now suppose someone asks, "Why isn't Joe pregnant?" The following is a perfectly correct DN Model "Explanation" of this phenomenon.

1. Taking birth control pills prevents pregnancy.
2. Joe takes birth control pills.
3. Therefore: Joe is not pregnant.

Although this is a sound deduction, it is obviously not a good explanation of why Joe is not pregnant. The explanation of his lack of pregnancy is that fact that he was born male, not that he happens to have decided to go on birth control.

What has gone wrong with the DN model of explanation? Perhaps one feature is that the law-phenomenon relationship is too weak on this account. The phenomenon (like pregnancy) must be more tightly connected to the lawlike statement (such as that birth control prevents pregnancy). In Joe's case, these two regularities were totally unrelated. So, perhaps the DN model is simply incomplete, and needs only to be supplemented with some further requirements.

The Statistical Relevance Model

One thought is that what's missing in the DN model is some notion of relevance. The length of a shadow isn't relevant to the explanation of why a flagpole has a certain height. The consumption of birth control pills isn't relevant to the explanation of why Joe isn't pregnant. So, if we can add in some sort of relevance requirement, perhaps we can fix the account.

But what exactly does it mean to be relevant? That's not such an easy question to answer. But one answer you can give is to say that it is statistical relevance.

Here is a classic example. Suppose we are considering a badly behaved kid, and ask, "Why is this teenager delinquent?"

Suppose someone does a little research on the region and find that in general kids have a 65% chance of being delinquent, but that there are two major factors that influence this: whether the kid is male (M) or female (F) and whether their residence is urban (U) or rural (R). In particular, there are four alternatives, each associated with the following probability of delinquency.

This allows us to explain the phenomenon by referring to the four categories in this partition. For example, if we are trying to explain the behaviour of an urban female, we can say that her delinquency is explained by the fact that \(\Pr(D|U \& F)=0.7\), i.e. that the probability of Delinquency (D) given that the person is Urban (U) & Female (F) is 70%. This is known as the Statistical Relevance Model of scientific explanation, introduced by Wesley Salmon.

On the Statistical Relevance approach, one explains a phenomenon by identifying the factors that influence its probability. Note that an essential part of this is being able to partition the possibilities into categories that influence the probability in a non-trivial way.

These probabilities provide one sense in which sex and location explain delinquency.

In particular, the four categories gave us information that changed the prior probability of delinquency from 65% to something else. Moreover, the categories were each associated with a different probability, allowing us to meaningfully compare them and say how one matters more than another.

The Statistical Relevance account also manages to avoid some of the shortcomings of the DN model. For example, in the pregnancy case, Joe's lack of pregnancy (P) is not influenced by the fact that he is taking birth control (B), but because he is male (M). We can write this,

\( \Pr(P|M\&B) = \Pr(P|M) = 0\).

In other words, taking birth control (B) is not statistically relevant, because it does not change the prior probability of Joe's pregnancy, which was already zero. On the other hand, if male to female (F) rates of pregnancy when taking and not taking birth control, we get a relevant partition.

\(\Pr(P|F\&B) > \Pr(P|F\& \neg B). \)

The trouble with the statistical relevance model is that statistical correlations are not always explanatory. For example, suppose we wish to explain why a house is burning down (B). We notice that there is a statistical correlation between burning houses and the presence of fire fighters (F). In particular,

\(\Pr(B|F) > \Pr(B|\neg F)\).

However, the mere presence of firefighters clearly does not explain why the house is burning. It might be the presence of faulty wiring, or of a careless smoker, or of an arsonist. But mere burning house is not explained by the mere statistical correlation between burning houses and firefighters.

This lesson is analogous to the well-known adage that correlation does not imply causation.

But might this be more than an analogy? One might take the problem with the Statistical Relevance model to be that an explanation must express a causal relationship, and statistical correlation is not enough for that.

Perhaps the Statistical Relevance account can simply be modified to account for this kind of problem, and I would encourage you to give it a try. Wesley Salmon himself considered it evidence that he had to completely start over, and instead proposed a new model of explanation that centred around a notion of causation.

The Causal Mechanistic Model

The Causal Mechanistic Model takes an explanation of a phenomenon to trace the causal processes leading up to the occurrence of the phenomenon and of the phenomenon itself. Salmon normally used "causal process" to refer to some motion and interaction that occurs continuously in time.

An example would be the explanation of the question, "Why did the billiard ball go in the side pocket?" To explain this, we must trace the causal process leading up making up this phenomenon.

Salmon characterised the processes that count as causal as those that have the ability to transmit a mark, where a "mark" is some piece of information or some other form of matter and energy. For example, the chalk from the cue stick may in principle be transferred to the cue ball, and then again to another billiard ball, as the transfer of energy in the process unfolds.

Compare this to the moving spotlight of a lighthouse, through which a mark cannot be transmitted.

The beam of light appears to be moving in a circle, although we know that it is not. It is simply the successive firing of straight lines of photons in rapid suggestion. A "mark" in the form of light energy is transferred from the bulb through the air, but the beam itself does not transfer a mark as it spins around.

The Causal Mechanistic account has the potential to explain how birth control is relevant to the pregnancy example, by identifying a chain of processes that begins with a birth control pill. It also provides a diagnosis of the flagpole example: a causal process involving the height of the flagpole gives the shadow its length; but no causal process involving the shadow gives the flagpole its height.

Thus, the Causal Mechanistic account seems to work well for simple mechanical systems. Unfortunately, it tends to founder in high-level complex systems such as in social or economic systems.

For example, Tickle Me Elmo was a toy introduced by Tyco toys in 1996, which became so popular that it sold in November with Tyco struggling to produce enough for the holiday season. As a result, Tickle Me Elmo (which retailed at $28.99 USD) sold for as much as $1500 USD in newspapers and on the internet.

Suppose we were to pick up a Tickle Me Elmo toy and ask, "Why was this toy so expensive?" There is not an obvious history of causal processes for any given toy that one can describe in order to explain its price. Rather, it seems to be explained by the higher-level law of supply and demand. This law is not so much about transmission of information and matter-energy as it is about relationships between supply, demand and price of a commodity.

The Unificationist Model

An alternative model advocated by Philip Kitcher is the unificationist approach. This approach involves a simple addition to the DN model, which is that an explanation should involve a unifying set of premises.

Think again about our paradigmatic explanation from the beginning, Newton's explanation of Kepler's laws.

1. Three laws of motion, together with inverse-square law of gravitation.
2. Further premises that the sun is approximately fixed in place, and a planet begins with some initial velocity perpendicular to the direction of the sun.

From this Newton deduced Kepler's laws.

But he could also deduce facts about many other things, from flying machines...

To bouncing springs...

To falling bodies near the Earth.

That is, Newton's laws compress a great deal of information into a very small expression.This is the central idea of the Unificationist model: the better the compression of information, the better the explanation.

This allows us to account for the flagpole example, albeit in a somewhat roundabout way.

Suppose we assume a rule of production, which explains the height of an object in terms of the way that it is produced. This would compress information about the height of a great many objects, including mountains, buildings, and flagpoles, into a rule describing how an object is produced.

Now suppose we add the length of a flagpole's angle, among other things, to my set of premises. This provides me with another way to calculate the height of the flagpole. But it is redundant: we already have a rule for explaining the height of the flagpole in terms of how it was produced. There are also typically objects oriented so as to have no shadow, for which the shadow calculation would not help. So, adding facts about the flagpole's shadow provides a poor compression of information. For this reason, according to the unificationist, the shadow is not a good explanation of the flagpole's height.

Still, in a room where events unfold in the presence of a few fixed lamps, a shadow may compress a great deal of information about the height of objects. But shadows still don't seem to provide a good explanation of height. According to Woodward, this account is still missing an essential ingredient that can be afforded only by causal information.

How and when to give an explanation

There is understandably still a great deal of debate as to how to characterise various kinds of explanations in science. The accounts we have seen provide a great number number of creative suggestions as to what matters when we try to explain things. So, you might use them as a useful guide to seeking explanations, and to knowing when an explanation has been given. When you wish to know why a phenomenon occurs, you might try to answer in one of the following ways.

You should now be able to think of the names for these four general strategies when you seek an explanation. There may of course be others (indeed, rest assured that there are), but these may get you started.

You may also wish to use some or all of these templates when considering whether or not some proposal really explains a phenomenon.

The Anthropic Principle

Some have suggested that the anthropic principle provides an explanation of many aspects of the observable universe. The anthropic principle states that the universe must be consistent with the hypothesis that human life occurs. (In the optional Earman article, this is known as the Strong Anthropic Principle or SAP.)

For example, the anthropic principle says that the universe must contain carbon-based molecules, since human life requires carbon-based molecules, and so a universe without them could not sustain human life.

But suppose we ask the question, "Why are there carbon-based molecules?" Can an appeal to the anthropic principle provide a good explanation? If the anthropic principle really is a lawlike statement, then perhaps it can, through something like the following.

1. Lawlike statement. The universe must be consistent with the hypothesis of human life.
2. Further premises. The occurrence of carbon molecules is essential for the hypothesis of human life.
3. Therefore: Phenomenon. There must be carbon based molecules.

Notably, the anthropic principle also appears to compress a great deal of information, and so perhaps satisfies the unificationist account in addition to the DN model.

However, this kind of anthropic explanation does not fare well under other models of explanation, and indeed, appears to be susceptible to many of the difficulties that plague the DN model of explanation.

If one wishes to trace a causal process through to phenomenon of carbon molecules, the anthropic principle provides none. A proper explanation would seemingly involve hypothesis about the elements produced when stars are formed, planet formation, and so on. The anthropic explanation above has none of those things.

Similarly, it is hard to see how one might find a statistical correlation associated with an anthropic explanation, since we do not have multiple universes at our disposal available to do statistical experiments.

The challenge of whether the anthropic principle provide a good explanation of a phenomenon thus appears to depend on what account of explanation one gives. Analysing it in terms of these accounts of explanation provides a variety of reasoned ways to say if an anthropic argument is an explanation, or whether would-be explainers of the occurrence of carbon ought to go back to the drawing board.