On the meaning of
Time Reversal
Bryan W. Roberts | LSE
Symmetries and Asymmetries in Physics
Leibniz Universität Hannover

Spatial translation has an operational implementation

Spatial rotation has an operational implementation

Time reversal has no operational implementation
What would it even mean to 'reverse' time?
Standard picture of time reversal
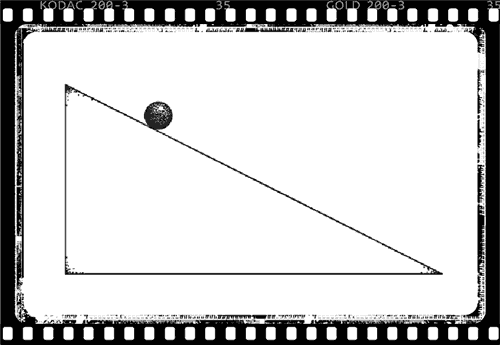
Imagine a 'film' of a process, and then reverse it.
Standard meaning of time reversal
\(t \mapsto -t\)
\((Q,P) \mapsto (Q,-P)\)
\(\sigma_z \mapsto -\sigma_z\)
\((E,B)\mapsto (E,-B)\)
\(\psi \mapsto T\psi\)
Physics Skeptics: Does \(T\) deserve the name?
"'reversal of the direction of motion' is perhaps a more felicitous, though longer, expression than 'time inversion'"
Physics Skeptics: Does \(T\) deserve the name?
"This is a difficult topic for the novice, partly because the term time reversal is a misnomer; it reminds us of science fiction. Actually what we do in this section can be more appropriately characterized by the term reversal of motion."
Physics Skeptics: Does \(T\) deserve the name?
"the term 'time reversal' is misleading, and the operation . . . would be more accurately described as motion reversal."
Philosopher Skeptics: Does \(T\) deserve the name?
"the books identify precisely that transformation as the transformation of 'time-reversal.' ... The thing is that this identification is wrong. ... [Time reversal] can involve nothing whatsoever other than reversing the velocities of the particles
Philosopher Skeptics: Does \(T\) deserve the name?
"David Albert . . . argues—rightly in my opinion—that the traditional definition of [time-reversal invariance], which I have just given, is in fact gibberish. It does not make sense to time-reverse a truly instantaneous state of a system"
Philosopher Skeptics: Does \(T\) deserve the name?
"time reversal should leave the states intrinsically untouched and just change their order. ... If we cleave to that understanding of time reversal, none of the counterexamples Roberts offers constitutes a failure of [Curie's Principle]"
Philosopher's complaint: things 'just lie there'
On this view, time reversal can do no more than reverse 'little \(t\)'
Why does time reversal matter?
The arrow of time
(Kaon decay)
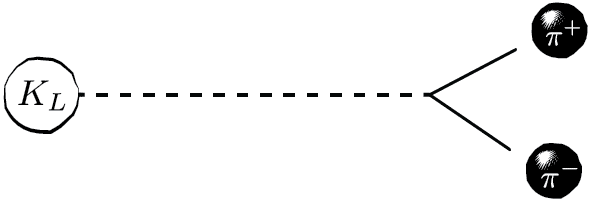
Statistics
(Superselection)
\(\phi^{fer}+\phi^{bos} = mixed\)
Nature of matter
(Kramers degeneracy)
time-symmetric fermions
Fermions: \([T,H]=0 \Rightarrow H\) is degenerate
\(\Rightarrow\) more magnetically susceptible
Animal Rights
(Painlevé 1904)

Thesis:
The standard meaning of time reversal (really! no need for 'motion reversal') can be derived from reasonable assumptions about the nature of time.
"Three Myths About Time Reversal..." (BWR 2017)
philsci-archive.pitt.edu/12305/
Two approaches
Temporal
Properties
of Matter
Temporal
Spacetime
Structure
Some intuition
On why things don't 'just lie there'
Intuition Pump 1.

A soldier running towards a monster is brave.
The time-reversed soldier is cowardly.
These are temporally oriented properties.
Intuition Pump 2.
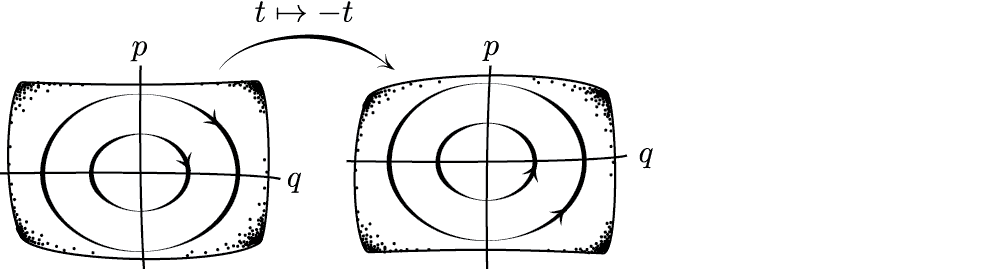
A harmonic oscillator is manifestly time reversal invariant.
Oscillator phase-space diagram

Albert-Callender-Castellani-Ismael 'Reversal'
Velocity and momentum in opposite directions!
Standard Time-Reversal
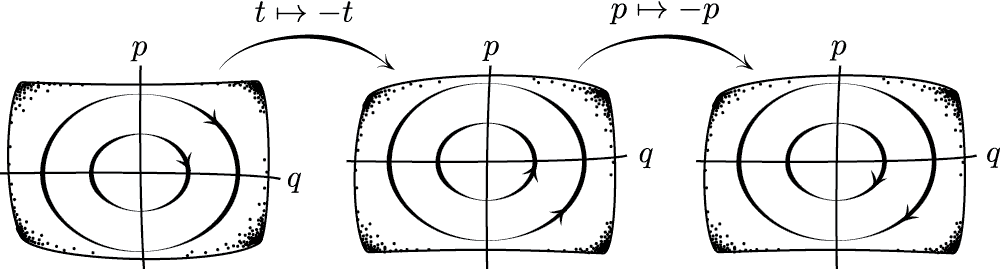
Velocity and momentum in the same direction (BWR 2013)
A three stage approach
Time reversal satisfies:
- Unitarity or Antiunitarity
- Antiunitarity
- Particular Transformation Properties
0th stage: What even counts as order-reversal?
- Standard Account: \(t \mapsto -t\)
- Peterson Reversal (2015 SHPMP): \(t \mapsto \tfrac{1}{e^{t}}\)
Both satisfy order-reversal:
\(t>t' \Leftrightarrow f(t) < f(t')\)
0th stage: What even counts as order-reversal:
- (1) Order reversal: \(t < t' \Rightarrow f(t)>f(t')\)
- (2) No 'Stretching': \(t\mapsto f(t)\) is linear
- (3) Involution: \(f(f(t))=t\)
Fact: (1)+(2)+(3) \( \Rightarrow \) \(f(t) = -t+t_0\) with \(t_0\in\mathbb{R}\)
Time-translation symmetry: can choose \(t_0=0 \Rightarrow f:t\mapsto -t\)
General Form of Time Reversal: \(\psi(t) \mapsto T\psi(-t)\)
Note that at this stage, \(T\) could be the identity
A three stage approach
Time reversal satisfies:
- Unitarity or Antiunitarity
- Antiunitarity
- Particular Transformation Properties
Unitarity:
(1) \(U^*U=UU^*=I\)
(2) \(U(a\psi+b\phi)=aU\psi+bU\phi\)
\(\Leftrightarrow
\langle U\psi,U\phi \rangle = \langle \psi,\phi \rangle \)
Antiunitarity:
(1) \(U^*U=UU^*=I\)
(2) \(U(a\psi+b\phi)=a^*U\psi+b^*U\phi\)
\(\Leftrightarrow
\langle U\psi,U\phi \rangle = \langle \psi,\phi \rangle^* \)
Wigner Thm gloss: If \(T\) preserves probabilities,
\[ |\langle T\psi,T\phi \rangle|^2 = |\langle \psi,\phi \rangle|^2, \]then \(T\) is unitary or antiunitary.
Wigner's Thm Precisely: Given a Hilbert space \(\psi\in\mathcal{H}\), Ray space \(\Psi\in \mathcal{R}\),
If \(\mathbf{T}:R\rightarrow R\) preserves ray-space probabilities,
\[\langle \mathbf{T}\Psi,\mathbf{T}\Phi \rangle = \langle \Psi,\Phi \rangle\]then \(\mathbf{T}\) is uniquely implemented by an operator \(T:\mathcal{H}\rightarrow\mathcal{H}\) that is unitary or antiunitary.
Uhlhorn's Thm: If \(\mathrm{dim}\mathcal{H}>2\) and \(\mathbf{T}\) is 'orthogonality preserving',
\(\Psi\bot\Phi\;\;\) iff \(\;\;\mathbf{T}\Psi\bot \mathbf{T}\Phi\)
then it is uniquely implemented by an operator \(T\) that is unitary or antiunitary.
Uhlhorn's Thm gloss: If 'mutual impossibility' is independent of the direction of time, then \(T\) is unitary or antiunitary.
\(T\) can reasonably be assumed to satisfy the premise.
Philosophers agree so far.
Albert-Callender-Castellani-Ismael:
\(T=I\) is the identity (and thus unitary)
A three stage approach
Time reversal satisfies:
- Unitarity or Antiunitarity
- Antiunitarity
- Particular Transformation Properties
Argument 1.
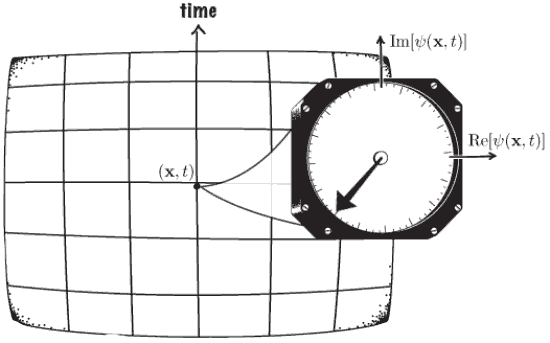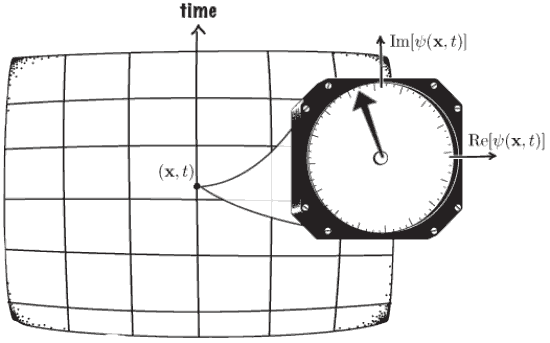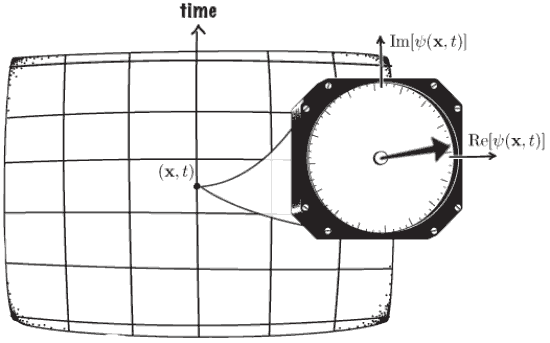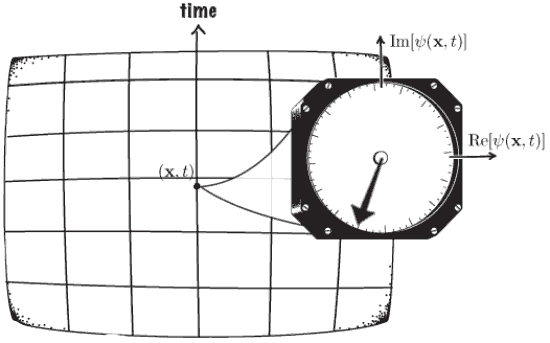
The phase of an energy eigenstate rotates in time, and should reverse under time-reversal. An antiunitary \(T\) is needed to reverse this; \(t\mapsto-t\) is not enough.
Argument 2. Let \(TQT^{-1}\) and \(TPT^{-1}=-P\).
\(Ti\hbar T^{-1} = T[Q,P]T^{-1}\)
\(= [TQT^{-1},TPT^{-1}] = [Q,-P]\)
\(= -i\hbar\)
\(T\) is not unitary \(\Rightarrow T\) is antiunitary
by our previous discussion
Classical analogue: Given a Poisson manifold \((M,\{\,,\,\})\), time reversal is anticanonical.
\(T:C^\infty(M)\rightarrow C^\infty(M)\) does not preserve the Poisson bracket. Rather: \[ \{Tp,Tq\}=\{-p,q\} = -\{p,q\} \]
Another approach
Time reversal invariance (TRI)
An invariance of a dynamical theory maps possible trajectories to possible trajectories
(An invariance preserves \(\mathrm{Sol}\subset\mathrm{Kin}\)).
Equivalent Statements about \((\mathcal{H},t\mapsto e^{-itH})\)
- \((\mathcal{H},t\mapsto e^{-itH})\) is time reversal invariant
- If \(\psi(t)\) is a solution, then \(T\psi(-t)\) is too.
- \(Te^{itH}=e^{-itH}T\)
Argument 3 (Theorem). Let \(T:\mathcal{H}\rightarrow\mathcal{H}\) be a (unitary or antiunitary) bijection. If there exists at least one self-adjoint \(H\) (densely defined) satisfying,
- (positive energy) \(\;0\leq \langle \psi,H\psi\rangle\)
- (non-trivial) \(\;H\neq0\)
- (\(T\)-reversal invariant) \(\;Te^{itH}=e^{-itH}T\)
Then \(T\) is antiunitary.
Proof. Condition iii) implies that \(e^{itH} = Te^{-itH}T^{-1} = e^{T(-itH)}T^{-1}\), which implies that \(itH = -TitHT^{-1}\). Now, suppose for reductio that \(T\) is unitary and hence linear. Then we can conclude from the above that \(itH =-itTHT^{-1}\), and hence \(THT=-H.\) Since unitary operators preserve inner products, this gives \(\langle\psi,H\psi\rangle = \langle T\psi,TH\psi\rangle = -\langle T\psi,HT\psi\rangle.\) But condition i) implies both \(\langle\psi,H\psi\rangle\) and \(\langle T\psi,HT\psi\rangle\) are nonnegative, so we have,
\[ 0 \leq \langle\psi,H\psi\rangle = -\langle T\psi,HT\psi\rangle \leq 0. \]It follows that \(\langle\psi,H\psi\rangle = 0\) for all \(\psi\) in the domain of \(H\). Since \(H\) is densely defined, this is only possible if \(H\) is the zero operator, contradicting condition ii. Therefore, since T is not unitary, it can only be antiunitary.
Consequence of denying antiunitarity: Even an system with no interactions would fail to be time-reversal invariant.
Earman (2004): "the symptom of a perverse view"
A three stage approach
Time reversal satisfies:
- Unitarity or Antiunitarity
- Antiunitarity
- Particular Transformation Properties
Question. Can we explain why:
\(Q\mapsto Q\)?
\(P\mapsto -P\)?
\(\sigma_z\mapsto -\sigma_z\)
Momentum generates spatial translations

\(e^{-iaP}(E_\Delta) e^{iaP}=E_{\Delta-a}\)
where \(Q=\int_{\mathbb{R}}\lambda dE_\lambda\)
Fact. Suppose the 'meaning' of time reversal does not depend on location in space:
\[e^{-iaP}Te^{iaP}=T.\]Then time reversal maps \(P\mapsto-P\)
Proof: \(e^{-iaP}=Te^{-iaP}T^{-1}=e^{T(-iaP)T^{-1}}=e^{iaTPT^{-1}} \;\Rightarrow\; TPT^{-1}=-P\)
Uniqueness is established in BWR 2017 Proposition 2
Fact. Suppose the 'meaning' of time reversal does not depend on orientation in space:
\[e^{-ia\sigma_z}Te^{ia\sigma_z}=T.\]Then time reversal maps \(\sigma_z\mapsto-\sigma_z\)
Uniqueness is established in BWR 2017 Proposition 3
Three places to get off the train:
- Mutual impossibility independent of time's arrow
\(\Rightarrow T\) is unitary or antiunitary - One non-trivial system is time symmetric
\(\Rightarrow T\) is antiunitary - Homogeneity, isotropy, etc. of time-reversal
\(\Rightarrow\) transformation rules for momentum, spin, etc.
Bonus Proposition!
\(P\)-invariance was replaced by \(CP\), then \(CPT\). Will we always have a replacement of the form \(UT\)?
Yes.
Proposition. For any quantum theory with a unitary dynamics \(t\mapsto e^{-itH}\), there exists a unitary operator \(U\) such that \(UT\)-invariance holds, where \(T\) is the (antiunitary) time-reversal operator.
Proposition. For any quantum theory \((\mathcal{H},t\mapsto e^{-itH})\), there exists a unitary operator \(U\) such that \(UT\)-invariance holds, where \(T\) is the (antiunitary) time-reversal operator.
Proof. Let \(T\) be the (antiunitary) time reversal operator. Let \(K\) be the (antiunitary) complex conjugation operator associated with \(H\), and define \(U := KT^{-1}\). Then \(U\) is unitary, since it is the product of two antiunitary operators. Moreover, \([K,H]=0\), and so \([UT,H]= [KT^{-1}T,H]=[K,H]=0\), which implies that the theory is invariant under \(UT\).
Thesis:
The standard meaning of time reversal (really! no need for 'motion reversal') can be derived from reasonable assumptions about the nature of time.
"Three Myths About Time Reversal" (BWR 2017)
philsci-archive.pitt.edu/12305/
fin

These slides were written in html using reveal.js
(Documentation and Download)
Two approaches
Temporal
Properties
of Matter
Temporal
Spacetime
Structure
Temporal Properties of the EM-Field

"[\(B\)] can no more just lie there than an angular velocity vector field can"; instead, \(T:B\mapsto-B\)
Spacetime structures in the EM-Field
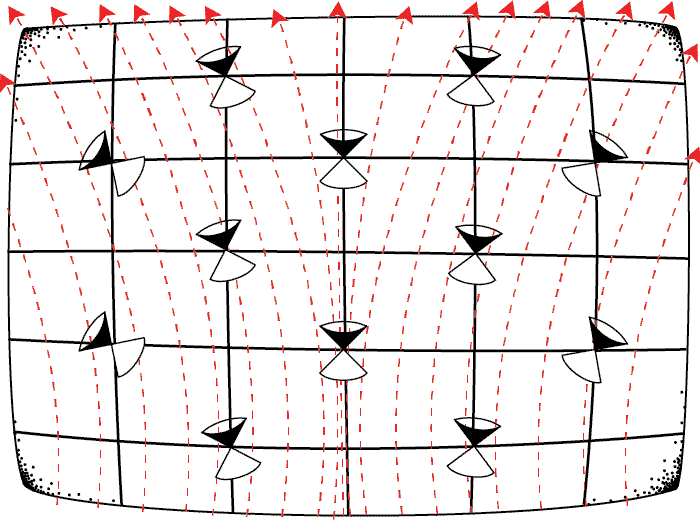
With a time orientation \(\tau^a\), let \(T:\tau^a\mapsto-\tau^a\)
Analyze the way \(\tau^a\) 'hooks up' to physical quantities to induce the transformation rules for time reversal.
- \(T:F_{ab}\mapsto -F_{ab}\)
- \(T:J^a\mapsto -J^a\)
- \(T:E^a\mapsto E^a\)
- \(T:B^a\mapsto -B^a\)
A quantum analogue:
Varadarajan 2000 Lemma 9.9
Theorem (Varadarajan). If \(\tau\) is time reversal in the inhomogeneous Lorentz group, and if a representation \(\alpha\) on \(\mathrm{Aut}(L)\) of a Hilbert lattice \(L\) satisfies,
- (a) (non-trivial) Rep of the translation subgroup is non-trivial; and
- (b) (positive energy) Spectrum is in the future light cone;
then \(T:=\alpha(\tau)\) is antiunitary.