Notes on Holes
Bryan W. Roberts
University of Southern California
ARLT-100: Einstein's Spacetime Revolution
Background Reading (Warning: Difficult!): Bryan's Notes on Holes
Fair warning: The conceptions of "holes" described below have nothing to do with black holes or with the hole argument. It is important not to confuse these three ideas!
1. Holes in spacetime: why they matter
What is a spacetime, exactly? You are familiar with a few of the basic features of a spacetime. A spacetime involves a manifold of "events," each representing a place at a time. You also know spacetime involves distance and time relations, which are captured by a particular kind of metric. And, a spacetime satisfies the laws of gravity, given by Einstein's Field Equations.
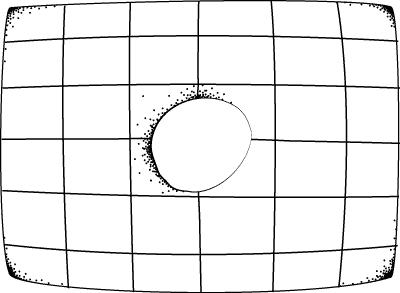 Our question today is about whether or not spacetime has "holes." To ask this question, we must first say a "hole" even means. The intuitive idea of a spacetime hole is just a missing point or set of points. There is a set of points that make up spacetime, just as there is a set of points making up a sheet of paper. And like a sheet of paper, we can imagine deleting some subset of the points, leaving a "hole" in their place.
Our question today is about whether or not spacetime has "holes." To ask this question, we must first say a "hole" even means. The intuitive idea of a spacetime hole is just a missing point or set of points. There is a set of points that make up spacetime, just as there is a set of points making up a sheet of paper. And like a sheet of paper, we can imagine deleting some subset of the points, leaving a "hole" in their place.
The difficulty with talking about a hole is that the hole itself does not occupy any point in space or time. It is impossible to say where or when there is a hole — it is nowhere and nowhen! So, our task is to try to define holes in spite of this difficulty.
Holes in spacetime matter because if they exist, then they there is a sense in which general relativity might be said to be "broken." Many think that a (non-quantum) theory is "broken" if it fails to be deterministic. (Recall that a theory is deterministic if the present state of the universe determines all future and past states.) If there are holes in spacetime, then determinism dramatically fails in general relativity.
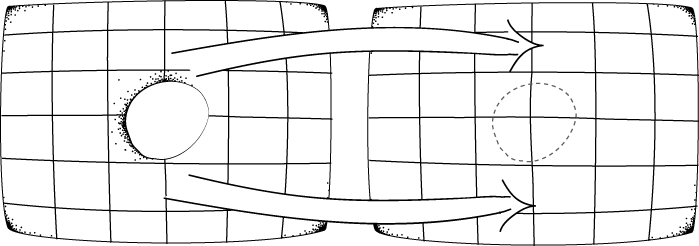
To see why, consider an object headed into the hole, like the butterfly below on the left. When the worldline of the butterfly reaches the hole, it stops. The butterfly ceases to exist in space and time. It blinks out of existence once and for all; no more butterfly.

The "time-reverse" of this trajectory is also possible, in which a butterfly popping out of the hole as in the figure above on the right. The trajectory has a finite past that begins at the hole, but continues to the future as normal.
But since just about anything can fall into the hole, it follws that just about anything can pop out. This led the philosopher of science John Earman to worry about the possibility that "all sorts of nasty things — TV sets showing Nixon's 'Checkers speech,' green slime, Japanese horror movie monsters, etc.— emerge helter-skelter" from the hole.
There are two main reasons that one might be led to pursue a more precise definition of what a "hole" is. The first is the militant reason: one might consider such violations of determinism to be non-sensical, and thus seek to eliminate them from the discourse of modern physics. The idea here is to define holes so that we can eliminate them. The second reason is descriptive: holes represent an curiosity and perhaps even a possibility in general relativity, and should be described as completely as possible in order to better characterize the world we live in.
Either way, it is important to have a definition of holes. Unfortunately, it is not so easy to define something that doesn't exist in space and time.
2. First pass at defining holes: extendibility
Our first attempt to define holes aims to capture the idea that a hole can be "filled in." However, the language of general relativity only allows us to talk about properties of points in spacetime. We cannot literally talk about "filling in" a hole, since there is nothing there to talk about filling in!
Instead, we will consider the property that all the points in spacetime can be mapped into a "larger" spacetime (i.e. not just a copy of the original spacetime) in a way that preserves the distance and time relations. Such a map is called an isometry. When a spacetime can be mapped by an isometry into a larger spacetime, we say that the original is an extendible spacetime. (Otherwise, it is inextendible.) We sometimes call the new spacetime an extension of the original.
Should spacetime be forbidden from being extendible? In other words, should the inextendibility of spacetime be considered a law of physics? John Norton argued that it should not, in his article "Observationally Indistinguishable Spacetimes: A Challenge for Any Inductivist," although this is up for debate.
I argue that inextendibility is a necessary presupposition of any good description of spacetime. In my view, one of the roles of spacetime is to describe the possible ways that test bodies can be arranged. Things can be arranged in certain places, with certain velocities, and it is the job of spacetime to describe these possibilities. Of course, not all possibilities will be realized in the actual description of space and time. But failing to allow for all possibilities is a recipe for absurdity. Yet in an extendible spacetime, some possibilities are by definition left out, namely, all the points in the extension that are not in the original spacetime. So, to ensure that all possibilities are described, I claim that we must require spacetime to be inextendible, as a basic supposition of spacetime physics.
Spend some time and think about this on your own. Try to develop your own arguments on whether or not spacetime should be inextendible. Whether you agree with Norton or with me is up to you!
3. Second pass at defining holes: local extendibility
If a spacetime is extendible, then it is reasonable to say it has holes. But what about the converse: are there inextendible spacetimes that still have holes in some sense?
The answer is "yes." Consider the example of Deutsche-Politzer spacetime, described by making two "cuts" in Minkowski spacetime, identifying the top-lip of the first with the bottom-lip of the second, then identifying the bottom-lip of the first with the top-lip of the second. You can do this with a sheet of paper, some scissors, and a piece of tape. If you do it right, the result is a flat spacetime with a "handle" coming out the bottom.

Deutsche-Politzer spacetime is nearly a perfect smooth surface, with no trace of the original two "cuts" involved in the construction — except for two points. The problem is that the edges of the cuts get pinched "infinitely tightly." (You may have noticed this pinching if you tried the scissors-and-paper construction suggested above.) The place where the spacetime gets pinched, represented by the little circles in the diagram on the left above, are a certain kind of hole. They are not points in the spacetime; a worldline bumping into one would simply cease to exist.
And yet, Deutsche-Politzer spacetime is inextendible. Those endpoints cannot be put back in. The reasons for this are somewhat technical, but it is enough for us to say that they have been "pinched too tightly" for this to be possible. Nevertheless, there is a clear (intuitive) sense in which Deutsche-Politzer spacetime contains holes.
Thinking about this kind of problem led Steven Hawking and George Ellis in their famous textbook to propose a second attempt at defining "holes." Their idea was to consider a new property called "local extendibility." To define this property, we need a to understand the idea of closure.
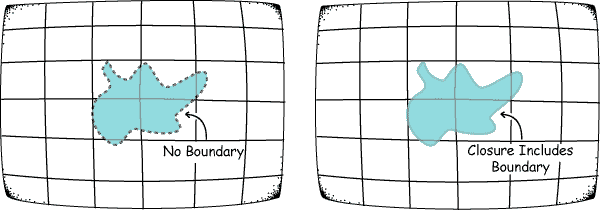 Take any open region, meaning a region without boundary. The closure of that region is just the original region plus the boundary. The blue region on the left in the diagram is an open region without boundary. The diagram on the right is the closure of that region, which includes the points on the boundary.
Take any open region, meaning a region without boundary. The closure of that region is just the original region plus the boundary. The blue region on the left in the diagram is an open region without boundary. The diagram on the right is the closure of that region, which includes the points on the boundary.
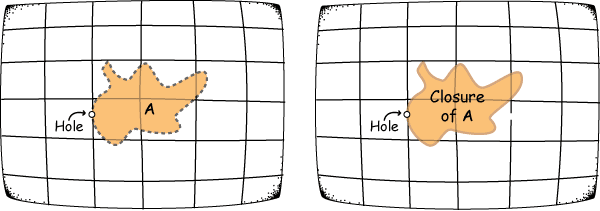
Hawking and Ellis noticed that, if a spacetime has holes, then you can normally find a region with an unusually "small" boundary. For example, consider the open region that just "touches" a hole in Minkowski spacetime, as in the orange region on the left. When we look at the closure of that region, we find that the boundary is smaller than we would expect. Namely, there is an "opening" on the boundary; this provides some intuitive indication that a hole is present.
 Hawking and Ellis needed to make this definition precise without explicitly mentioning the "hole." (Remember, there is no "hole" there to mention!) So they said a spacetime is locally extendible if it contains a region whose closure is not "compact" (which is a fancy way to say there is at least one "limit" point are missing from the boundary), but which can be extended to a region whose closure is compact (i.e. which has no missing limit points on the boundary). As an exercise, you should try to check that the spacetime containing the orange region above is locally extendible!
Hawking and Ellis needed to make this definition precise without explicitly mentioning the "hole." (Remember, there is no "hole" there to mention!) So they said a spacetime is locally extendible if it contains a region whose closure is not "compact" (which is a fancy way to say there is at least one "limit" point are missing from the boundary), but which can be extended to a region whose closure is compact (i.e. which has no missing limit points on the boundary). As an exercise, you should try to check that the spacetime containing the orange region above is locally extendible!
I have argued that we should always require spacetime to be inextendible. Should we also require that spacetime be locally inextendible? Unlike inextendibility, local inextendibility turns out to be deeply implausible, although this was not obvious when Hawking and Ellis suggested it in 1973. In 1980, John Beem proved the surprising result that Minkowski spacetime fails to be locally inextendible! The proof of this is given in the technical notes linked at the beginning of this document; I won't go into it here.
We certainly wouldn't want to say that Minkowski spacetime has holes. Moreover, Beem's argument generalizes easily to the result that no spacetime is locally inextendible. So, local extendibility cannot possibly provide us with a reasonable definition of "holes," since this would imply the absurd claim that every spacetime has holes.
Without local extendibility, we need another way to express the sense in which Deutsche-Politzer spacetime has holes.
4. Third pass at defining holes: "hole freedom"
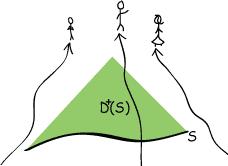 Our third way to define holes involves an important concept in spacetime physics called the domain of dependence. A domain of dependence is associated with every open surface that whose points cannot be connected by a timelike curves (such as a spatial surface). It is the region of points to the future of such a surface S such that any body traveling a timelike (or lightlike) curve in that region must have passed through S itself at some time in its past.
Our third way to define holes involves an important concept in spacetime physics called the domain of dependence. A domain of dependence is associated with every open surface that whose points cannot be connected by a timelike curves (such as a spatial surface). It is the region of points to the future of such a surface S such that any body traveling a timelike (or lightlike) curve in that region must have passed through S itself at some time in its past.
For example, if S is the open surface indicated in the diagram to the right, then the domain of dependence, written D+(S), is the green region. No future-directed timelike line can reach D+(S) without first passing through S; to do otherwise would be to travel faster than the speed of light. The idea then is that everything in D+(S) "depends" on events in S, and nothing else.
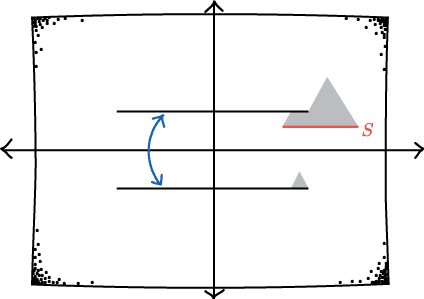 Our third attempt to define a spacetime with a hole is the following. Say that a spacetime is hole-free if it is impossible to make any surface (with no timelike curves in it) have a "bigger" domain of dependence by mapping that surface into another spacetime.
Our third attempt to define a spacetime with a hole is the following. Say that a spacetime is hole-free if it is impossible to make any surface (with no timelike curves in it) have a "bigger" domain of dependence by mapping that surface into another spacetime.
To get a better idea this means, let's return to Deutsche-Politzer spacetime. You can show that it is not hole free. To see this, draw in the spatial surface S indicated to the left. Its domain of dependence is the pair of pointy-regions indicated in gray. (You should verify this; argue that the gray region contains the all the points that can only be reached by passing through S.)
Is it possible to map S into another spacetime in such a way that the domain of dependence gets bigger?
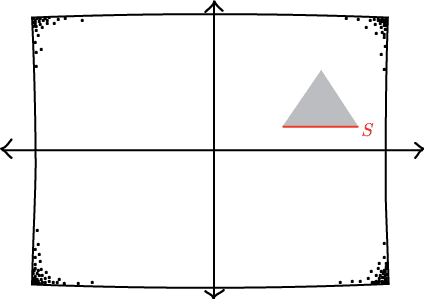 Of course it is. Just map S into normal Minkowski spacetime. The domain of dependence is much bigger in this spacetime, because it isn't bumping into the "handle" as it was before.
Of course it is. Just map S into normal Minkowski spacetime. The domain of dependence is much bigger in this spacetime, because it isn't bumping into the "handle" as it was before.
If you're interested in the official technical definition of what it means to make the domain of dependence bigger: this means that there is an isometry (as defined above) from the original domain of dependence into the new one, in such a way that the two domains of dependence are not identical. This is a technical detail, but one that you might take interest in if you decide to work more on this topic.
Local extendibility didn't work to provide us with an appropriate definition of holes. Does hole-freedom finally provide us with our definition? It might seem plausible on the face of it. But hole-freedom is just as implausible as local inextendibility: it turns out that Minkowski spacetime fails to be hole-free, too! The proof of this was pointed out in 2009 by Sergei Krasnikov. So, for the same reasons as before, this doesn't seem to work as a definition of what it means for a spacetime to lack holes.
How then are we supposed to define holes? It is an open problem in the philosophy of physics, which I leave that up to you! No final answer has yet been generally accepted. One promising route forward has been suggested by Manchak, involving a definition of holes that he calls "effective incompleteness." But the problem of defining holes remains very much open for fresh new ideas.
What you should know
- How "holes" are related to determinism, and why it is important to understand them.
- The definitions of closure and domain of dependence.
- What an extendible spacetime is, the arguments for and against requiring inextendibility.
- Examples of extendible and inextendible spacetimes.
- What a locally extendible spacetime is and what a hole-free spacetime is, and examples of spacetimes that fail to satisfy each.
 Our question today is about whether or not spacetime has "holes." To ask this question, we must first say a "hole" even means. The intuitive idea of a spacetime hole is just a missing point or set of points. There is a set of points that make up spacetime, just as there is a set of points making up a sheet of paper. And like a sheet of paper, we can imagine deleting some subset of the points, leaving a "hole" in their place.
Our question today is about whether or not spacetime has "holes." To ask this question, we must first say a "hole" even means. The intuitive idea of a spacetime hole is just a missing point or set of points. There is a set of points that make up spacetime, just as there is a set of points making up a sheet of paper. And like a sheet of paper, we can imagine deleting some subset of the points, leaving a "hole" in their place.


 Take any open region, meaning a region without boundary. The
Take any open region, meaning a region without boundary. The  Hawking and Ellis needed to make this definition precise without explicitly mentioning the "hole." (Remember, there is no "hole" there to mention!) So they said a spacetime is
Hawking and Ellis needed to make this definition precise without explicitly mentioning the "hole." (Remember, there is no "hole" there to mention!) So they said a spacetime is  Our third way to define holes involves an important concept in spacetime physics called the
Our third way to define holes involves an important concept in spacetime physics called the  Our third attempt to define a spacetime with a hole is the following. Say that a spacetime is
Our third attempt to define a spacetime with a hole is the following. Say that a spacetime is  Of course it is. Just map S into normal Minkowski spacetime. The domain of dependence is much bigger in this spacetime, because it isn't bumping into the "handle" as it was before.
Of course it is. Just map S into normal Minkowski spacetime. The domain of dependence is much bigger in this spacetime, because it isn't bumping into the "handle" as it was before.