Notes on Observational Indistinguishability
Bryan W. Roberts
University of Southern California
ARLT-100: Einstein's Spacetime Revolution
Background Reading: Norton on Observationally Indistinguishable Spacetimes
1.1. Deductive inferences in a scientific theory are inferences to the logical consequences of a theory. They are typically mathematical results that are guaranteed to be true whenever the assumptions of the theory are true.
Examples of Deductive Inferences:
1.2. Inductive inferences in a scientific theory are that are not logical consequences of the theory, but which we nevertheless are warranted to infer.
Examples of Inductive Inferences:
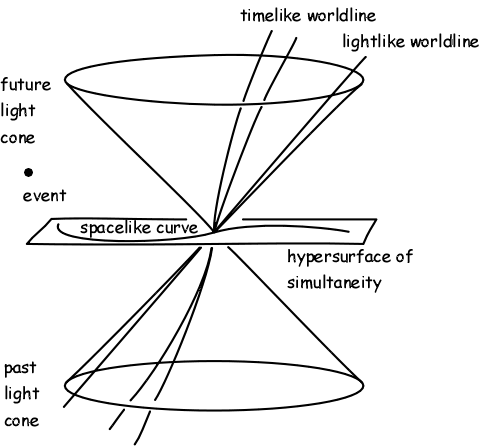
2.1. What can you know about the spacetime you're in? Answer: You can know at most everything in your past light cone.

More optimistically: You can aggregate information from a number of observers, including yourself, over the course of your lifetimes. Each ``observation'' will be a description of an observer's past light cone at a moment. Like this:
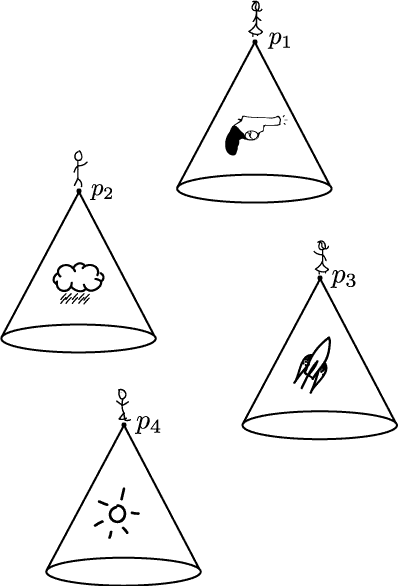
2.2. The problem is that no matter how many such observations you have, a recent discovery due to John Manchak shows that there are always at least two different spacetimes that are compatible with those observations. If a spacetime is such that any collection of its past light cones can be mapped onto a distinct spacetime in a way that preserves the distance relations on the light cones, then the two spacetimes are said to be Observationally indistinguishable.
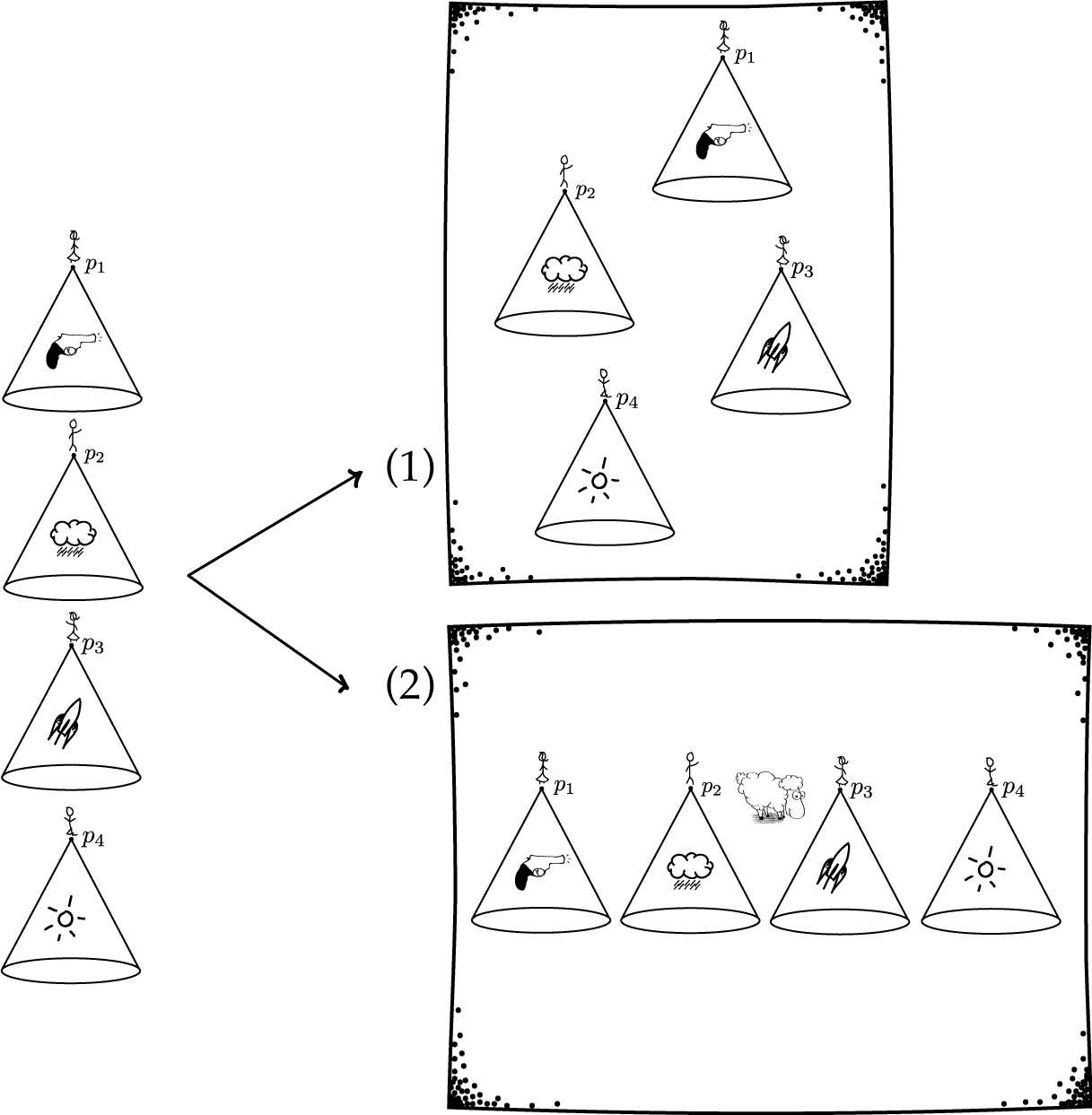
The most important result in this regard is Manchak's theorem: In spacetimes with no closed timelike curves, no number of observations is enough to know which spacetime we're in -- even assuming Einstein's equation and other local assumptions within general relativity!
Because of the way this theorem works, it is not only the case that we cannot deductively determine which spacetime we're inhabit within the context of general relativity. But as Norton argues, our best attempts to inductively determine which spacetime we're in also seem to fail as a consequence of Manchak's theorem. Can you see why?