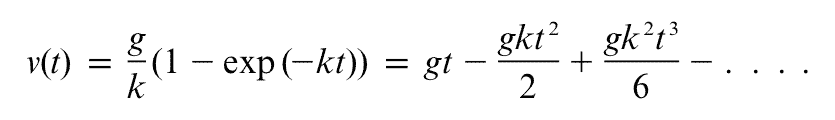Nothing is as we say it is
Many of us had to memorise Newton's laws when we were younger. Thankfully, they're so darn memorable! Do you remember the first one? Newton wrote it like this (but in Latin of course):
Newton's Law I. Every body preserves its state of rest, or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed thereon.
This is sometimes called the law of inertia. Being inertial means one of two things: you are either at rest without any forces acting on you, or moving with constant velocity without any forces acting on you.


Newton's Law I applies to all and only inertial systems. That seems helpful at first, until you realise that there are no inertial systems in our world. There are always forces acting on things: gravity, electricity, or magnetism. You could try to escape by heading out into the outer reaches of space, but even then you wouldn't be truly inertial. There would always be a tiny gravitational effect.

(Note for experts: The situation in general relativity, our modern theory of gravity, is no better. There, the analogue of Newton's first law applies only to test particles, meaning massive particles that occupy only a point in space, and do not exert any gravitational influence. But every massive body exerts some gravitational influence! So, there are no true test particles, and the law is strictly vacuous.)
The law of inertia involves an idealisation a statement that is strictly inapplicable in its description of the real world, but nevertheless thought to capture some important aspect of reality. They are everywhere in science. Almost nothing is exactly as we say.
How is it possible that a correct law of nature can fail to apply in general? How can it be a law when bodies are always changing their state of motion in practice? How should this influence our perspective on science? These are the puzzles that we'll be considering today.
Idealisations are the rule, not the exception
Almost every law or model in science is idealised in one sense or another. In a moment we will discuss some of the different ways that an idealisation can occur. But first, can you think of any examples that you might have encountered before?
Here's one. Idealisations are very common in the social sciences. For example, people participating in economic systems are often assumed to be rational in order to derive their preferences, or in order to predict the behaviour of a market. One often even assumes that human preferences satisfy a set of mathematical statements like the von Neumann-Morganstern axioms, thought to characterise how a rational human should behave. Perhaps we should behave that way, but unfortunately humans are often irrational, perhaps more often than we'd care to admit. Nevertheless, these models serve as an effective guide to describing social groups.
Another example: when biologists model the way that a population of foxes and hares is changing, they will typically treat all animals of the same species as identical. Of course they are not. Some animals are more effective predators than others, some are non-hunting babies or adolescents, and some will stray from the group and die of natural causes. However, the models still provide effective tools to describe the rough behaviour of the group.
Even a description merely representing things using real numbers involves many radical idealisations. Real numbers are perhaps the most familiar manifold of points, which we use all the time to represent our weight, our driving speed, or our location in space. But the real numbers also have many bizarre properties, such as the Banach-Tarski construction. This construction provides an algorithm for decomposing a real-valued sphere into a finite number of disjoint pieces (originally six pieces), and then reassembling it into two spheres of the same size as the original! It is a strange and unrealistic feature of representations using real numbers, that is made possible by considering what is known as an unmeasurable set.

These idealisations are more than merely incorrect descriptions. What's curious about them is that there is something about them that these descriptions get right in spite of their strict falsehood. We would like to understand what exactly that is. But to begin, let's discuss a few particular features that idealisations may have.
Formal vs Empirical Idealisations
To begin to understand idealisations more seriously, the historian and philosopher of science Ernan McMullin identified two broad classes of idealisations, which have sense been influential in their description.
He called the first a formal idealisation, where 'formal' refers to a scientific theory. These idealisations occur when concepts in a scientific description are either simplified or removed.
For example, in many scientific theories involving the earth, such as our theories of gravity, the earth is idealised as a sphere. But you may know that it is more nearly an ellipsoid, which bulges a little bit around the equator. But it gets worse: the ellipsoid description idealises away the description of the large bulging undulations that the oceans known as the geoid. And even that idealises away the irregularities formed by irregularly shaped matter on the surface such as ourselves. Our formal descriptions of the earth are full of idealisations!

The second class of idealisation is called a causal or empirical idealisation. McMullin uses the word "causal," which is unfortunate, because it brings in an unnecessary ambiguity about the meaning of a "cause." To avoid this, let us use the word "empirical" instead. These are idealisations that involve ignoring unnecessary or undesirable parameters in an experiment.
For example, Galileo argued that all bodies near the earth will fall in the same way. In particular, two bodies that fall from rest at the same height will reach the ground at the same time, regardless of their mass, shape or size. You can do this experiment yourself by dropping a book and a heavy pencil from the same height.
But Galileo's experiment involves many experimental idealisations. The color, shape and temperature of the body are all ignored. Some of these have no effect on the experimental outcome, but some of them do. In fact, the shape of a body can have a dramatic impact when it results in significant air resistance.
In order to remove the experimental idealisation, one might try to remove the air from a room, as Brian Cox does in this NASA spacecraft testing chamber.
After the test-chamber is evacuated there remain 2 grams of air in there. That may not seem significant, and is a fairly accurate way to describe low-orbit space environments near the earth. But it's still enough to ruffle the feather a little bit, it's a lot more atmosphere than the moon, where in a comparable room there would be about a hundredth of a microgram of atmosphere. A less-idealised test was actually given several decades ago during the 1971 Apollo 15 mission.
There are many further kinds of idealisations that could be mentioned. McMullin suggests that a further "material idealisation" occurs when one leaves out irrelevant parameters in a description, such as in the theoretical statement of Galileo's law without a description of colour or shape. He further suggests that empirical idealisations can apply to both real experiments and to thought experiments. We will set this latter possibility aside for now, and come back to it in a later lecture. You should feel free to explore the taxonomy of what it means to be an idealisation further on your own.
For now, let us turn to a helpful recent distinction that was recently introduced, which expresses a view about what an idealisation is not.
Approximation and Idealisation
John Norton (2011) has argued that there are important philosophical consequences in distinguishing what an idealisation is not. He begins by distinguishing the concept of an idealisation from an approximation. For Norton, that distinction is the following.
An approximation is an inexact description of a target system.
An idealisation is a real or fictitious system, distinct from the target system, some of whose properties provide an inexact description of some aspects of the target system.
Norton suggests we begin by picking out a target system that we wish to describe, and then ask whether our description refers to that system (in which case it's an approximation), or to some other system (in which case it's an idealisation). For example, suppose our target system is a falling skydiver.