Descriptions can be mechanical, pictorial, or linguistic. But however they are formed, our question will be about what it means for a description in science to represent or be a representation of the natural world. In particular, we will ask,
- How representations work, and
- Why they work so well in science.
The 'Most Naïve View'
Nelson Goodman dubbed one commonly held account of representation the 'most naïve view':
'Most Naïve View' of Representation. A represents B if and only if A appreciably resembles B.
This definition is plausible at first glance. For example, we admire the ability of paintings in the realist and hyperrealist traditions to accurately represent the world.

A first difficulty with this view is that representation is asymmetric, while resemblence is not. That is, the painting Steam Power and the trains in Chicago bear a resemblence to each other. But although the painting is a representation of the trains, it seems incorrect to say that the trains are a representation of the painting.
There is more reason to think that resemblance cannot be the whole story. Some representations are interesting because they are not realistic. For example, consider van Gogh's self-portrait in comparison to a modern artist's attempt at a more realistic representation. The more accurate resemblance probably would not have adequately served van Gogh's purpose.

Similarly, the following cartoon of the Earth in 1805 as a plate of plumb pudding in front of William Pitt and Napoleon Bonaparte is not an image of how the world really looks, but is still an interesting representation.

What this means is that distortion can be necessary in order for a representation to serve its purpose. For example, when one has a very tall sculpture, the proportions of the sculpture would not appear incorrect to us from our perspective on the ground. In order for the statue to have the correct appearance to us, it must be distorted.
A famous example of this is Holbein's Ambassadors. A distorted image at the bottom of the painting is difficult to make sense of when looking at the image straight on. But look at it from the side — literally look down the edge of your computer screen from the top-right corner — and you will see a photo-realistic image of a skull.

So, many descriptions represent because they do not resemble their source exactly. But conversely, there are also descriptions that resemble but do not represent a source.
A well-known example is the optical illusion of the shadow on the chess board.

In the image, Square A provides a representation of a dark square on a chessboard, while Square B provides a representation of a light square. In this sense, they do not represent the same thing. And yet, although you may not notice it at first, they are exactly the same colour.

These considerations suggest that, contrary to the 'most naïve view', representation is not a matter of resemblence, in that resemblance is neither necessary nor sufficient to have a representation. So, what is a representation?
The Of-As View of Representations
A view that goes back to the American pragmatist Charles S. Peirce takes representations to be an a relationship between a target and a source with a particular aim. This is referred to by van Fraassen as the 'Of-As' view of representations. On this view, the canonical expression of a representation is as follows.
Of-As View of Representation. A representation necessarily involves at least 3 components, X (the source), Y (the target), and Z (the use), which are expressed in the form, 'X is a representation of Y as Z'.
The Of-As view entails that it makes no sense to ask only if X is an accurate representation of Y, or even if it is a representation at all. It makes no sense to ask whether this image is an accurate representation of Taylor Lautner. We can only ask whether it is an accurate representation of Taylor Lautner as an alpaca. We can only have a representation of something, as something.

To take a someone more subtle example of how specifying a representation requires specifying a use, consider this famnous photograph of NY construction workers.

What does it represent? The answer depends on what we're using it for. An obvious answer is that it represents a group of men in 1932 having lunch during the construction of the Rockefeller Center skyscraper.
However, it is also a representation of a famous photograph, the author of which might be a man named Charles Ebbets, but which is not really known. A documentary about the photograph would use the very same image to represent a photograph, rather than the men themselves. It just depends on the use we have in mind.
Notice that, unlike the Naïve view, the Of-As view of representation gives what a representation requires, rather than a definition. So, the Of-As view of representation is principally an expression of what a representation is not. In particular, it is not just a relationship between two objects, or even a relationship of accuracy. It is a relationship that is relative to an aim or use.
The question then remains as to how the relationship expressed by a representation occurs. Suppose I think of a representation, following the Of-As view, in terms of a diagram like the following.
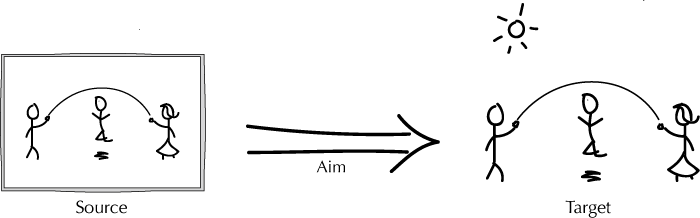
Then the question is, what exactly is the arrow, and how does it work? This is tied up in many difficult questions about reference and the philosophy of language, and you are encouraged to think it through. But let us first turn to a question of why it's so hard.
The unreasonable effectiveness of mathematical representations
Thinkers have for a long time expressed wonder about a certain kind of encounter with mathematics.
"... it is mathematics which reveals every genuine truth, for it knows every hidden secret, and bears the key to every subtly of letters; whoever, then, has the effrontery to study physics while neglecting mathematics, should know from the start that he will never make his entry through the portals of wisdom." (Thomas Bradwardine, 14th c.)
"[Natural] Philosophy ... is written in the language of mathematics, and its characters are triangles, circles, and other geometrical figures, without which it is humanly impossible to understand a single word of it; without these, one is wandering around in a dark labyrinth." (Galileo, 17th c.)
"It is positively spooky how the physicist finds the mathematician has been there before him or her." (Steven Weinberg, 20th c.)
There have been countless episodes in which mathematical tools were developed for one reason or another, and then turned out to be perfectly suited for science, apparently by complete concidence.
How is it possible for mathematics to provide such perfect representations of the natural world for use in science? This question is ssometimes referred to as Wigner's question, following a famous article written by the mathematical physicist Eugene Wigner called, "The unreasonable effectiveness of mathematics in the natural sciences." This is the question that we will turn to now.

First, we should note that the possibility of using a tool for a purpose is not so puzzling. For example, a screw-driver designer might make dozens of different kinds of screwdrivers with no particular screw in mind.

It wouldn't be so surprising if one particular screwdriver just happened to fit a screw that was actually made after the screwdriver. That's because it was the aim of the manufacturer to make screwdrivers that are able to turn screws.
Similarly, the effectiveness of mathematical representations in science would be no surprise if the aim of the mathematician were to produce tools for physics. Even if the mathematical tools were created with no particular model in mind, the shared aim would do a great deal to explain their effectiveness.
What makes Wigner's question so puzzling is that mathematics and the sciences appear to have very different aims. Being a mathematical physicist, Wigner focuses his attention on the comparison of mathematics and physics. According to Wigner,
- The aim of mathematics is to develop concepts that allow for simple, striking, brilliant arguments, whereas,
- The aim of physics is to discover patterns in the world by eliminating irrelevant properties.
Let's briefly comment on each of these.
The simple, striking, brilliance of maths
A famous example of a simple, striking, brilliant argument is Euler's solution to the problem of the Königsberg Bridges.
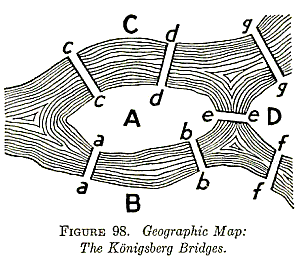
Many had observed that it seemed impossible to take a journey that allowed one to pass over each of the 7 bridges in Königsberg exactly one time. Try it a few times! If you're persistent, you might end up trying for a very long time.
The task turns out to be impossible. But how can one prove that? The mathematician Euler found a way, which is an exceedingly striking and beautiful argument.
First, one reduces each of the land masses to a point, and represents the bridge connections between land masses as lines between points.

If each bridge is crossed exactly once, then a typical bridge will have two lines emerging from it: the entering line and the exiting line. This means that a typical node must have an even number of lines emerging from it. Only the starting point and the ending point avoid this requirement.
However, the nodes in this bridge model all have an odd number of lines emerging from them. So, it is imposssible to traverse each bridge exactly once.
It is a simple, striking mathematical argument, and it gave birth to modern graph theory. But it was not designed with any particular science in mind. And yet, graph theory has now turned out to be essential to many areas of science, from physics to neuroscience to economoics.
Another example is that of a mobius strip. The simple, elegant theory of topology allowed us to understand this object, and explain its many strange properties.
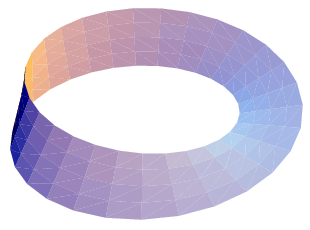

The analysis of topology led to a myriad of developments in science, most notably in the theory of space and time. But this was not the aim of topological analysis when it was first invented.
The impoverished patterns of science
According to Wigner, the aim of physics is very different from mathematics. It is about formulating laws, which Wigner describes as patterns in which information is systematically left out.

For example, Galileo's law of fall, alleged (though probably wrongly) to have been confirmed at the Leaning Tower of Pisa, says that all bodies experience freefall in the same way.
This representation of a falling body eliminates most of the facts about the body: mass, shape, size, colour, temperature, etc. Instead, the law represents the world in an interesting way by focusing on only a few relevant facts, such as the height of the body. This, according to Wigner, is what is characteristic of laws.
Some remaining questions
We have seen one puzzle about how it is that representations connect to reality. We now have a second: why are mathematical representations developed with completely different aims so pervasive in theorizing about the natural world?
The trouble is that there is no obvious reason for the aims of mathematics and science to align. It appears that they need not. Patterns in the world don't appear to require simple, striking, brilliant mathematical arguments, and such arguments don't require any patterns in the world. So, why should these two fields grown up to have so much in common?
This is a question I leave to you.
















