The world of the unobservable
Sometimes it is not the contents of reality but the very concept that fills one with wonder. Wittgenstein wrote about it:
the idea of one particular experience presents itself to me which therefore is, in a sense, my experience par excellence .... I believe the best way of describing it is to say that when I have it I wonder at the existence of the world. And I am then inclined to use such phrases as "how extraordinary that anything should exist" or "how extraordinary that the world should exist. (Wittgenstein 1965 Lecture on Ethics)
Of course, philosophers have often doubted the world exists, as in the old philosophical question, if a tree falls in the forest and nobody observes it, does it make a sound?

This question is significant. But, for the moment, let us join Wittgenstein in accepting that the world exists. After all, there is a variety of evidence regarding trees in the forest, not least of which includes loggers hacking away in the forest and noticing that trees make a sound when they fall. Collecting all this evidence together, and pushing on as best we can past the problem of induction, one may reasonably conclude that trees make a sound if they fall, whether or not anyone sees it.
Indeed, when a tree falls in the forest and nobody is around, it sounds like this:
So, from a scientific perspective, trees falling in the forest are a question we may set aside. But here is a harder question, which is harder to set aside: What about things that has yet to be observed? Or those that will never be observed? It is less obvious whether or not we could ever really know something about an unobservable world.
Why would anyone ever seriously posit the existence of such a hidden reality? Because a very authoritative source seems to do so all the time: science. So, this is often called the question of scientific realism:
Question. Are the unobservables posited by our best scientific theories true descriptions of the world (at least approximately)?
For example, current models of cosmology suggest that there is a subtle and invisible fluid that fills all of space, which is only detectable through its effect on the way the universe is expanding. That fluid is called dark energy. Nobody has ever directly observed dark energy, and probably nobody ever can, because there is too little of it to notice. So, is dark energy real?

Visible matter-energy in the form of light emitted from a nebula, which is thought to make up a tiny minority of the total matter-energy in the universe compared to dark matter.
Of course, when your friend makes up a good story, this doesn't mean you ought to believe it. But we're talking about no ordinary friend, and no ordinary story. Scientific descriptions are some of the most reliable stories you'll ever hear.
Some Dramatic Successes in Science
Science is perhaps one of the most successful enterprises that humans have ever engaged in. Successful in what sense? Well, science has lots of aims, and successfully achieves many of them. Here are just a few examples:
- Science predicts new phenomena with incredible accuracy.
- It explains many of the things we do observe.
- It unifies seemingly disparate phenomena, showing how they often arise from one and the same thing.
- It systematically dispels many myths and fallacies.
- etc.
Let's just think about the first kind of success, namely successful prediction: Le Verrier used Newton's theory of gravity to correctly predict the existence and location of Neptune. Einstein used General Relativity to predict that light bends as it passes near a massive body. These are just a few of countless examples in which scientific predictions shocked the world with unexpected and unparalleled accuracy.
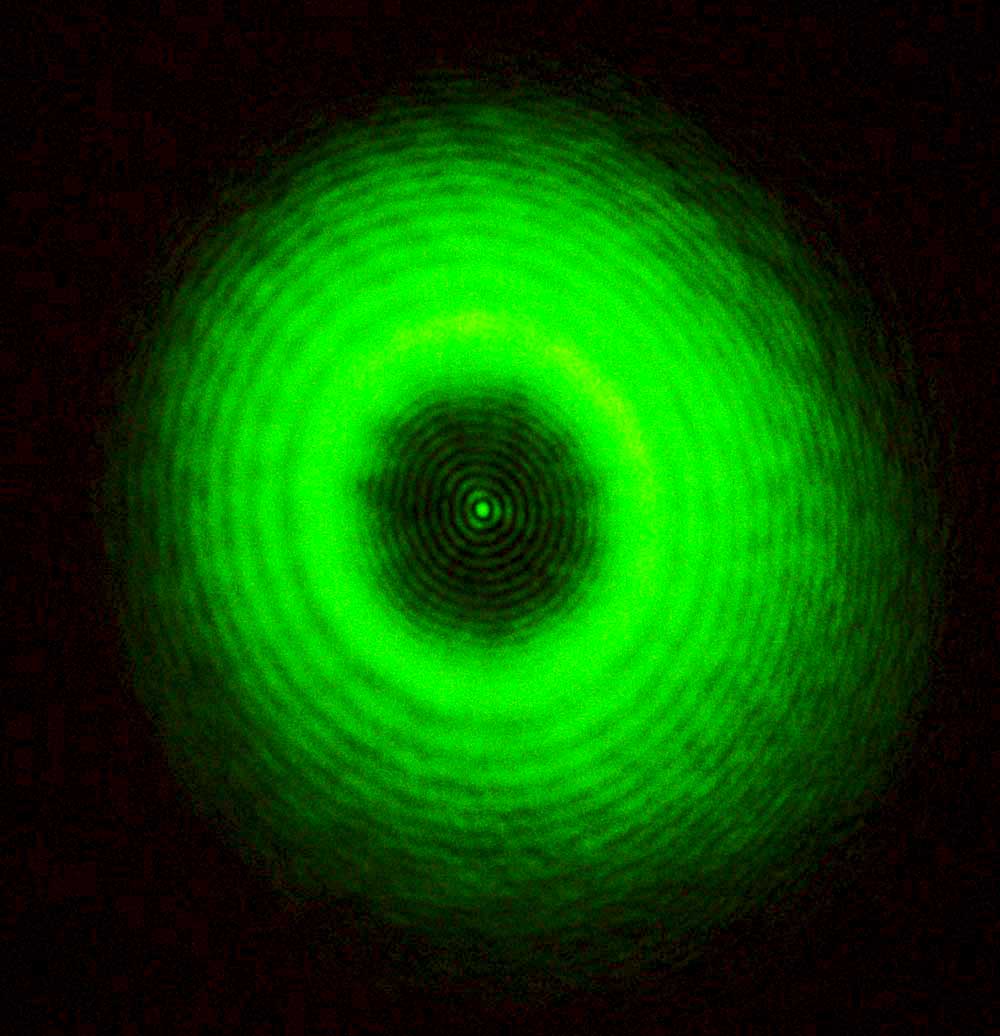
Here is another dramatically successful prediction in science: the prediction of the Fresnel-Poisson spot.
Augustin-Jean Fresnel (1788-1827)
In 1818, a young French engineer named Augustin-Jean Fresnel submitted a new theory of light to a science competition at the French Academy. Fresnel's theory proposed that light is a wave, rather than a particle as had been believed since the time of Newton.
One of the evaluators for the contest was the distinguished mathematician Siméon Poisson, who was skeptical about Fresnel's proposal. So, he set out to argue that the proposal must be false. After doing a little calculation Poisson discovered that, unbeknownst to Fresnel, the theory made the following absurd prediction: if you place a very small circular obstruction in front of a light source, then you would see a spot of light right in the middle of the shadow.
This was not quite enough to refute Fresnel's theory; a test had to be done. So, the chair of the competition decided to set up an experiment to check this strange prediction. To everyone's surprise, the predicted spot appeared clear as day. It was an incredible predictive success, and Fresnel was declared the winner of the competition.
No Miracles
Nobody could observe Fresnel's light wave propagating the way we observe water waves propagating. Nobody could see the curvature that Einstein claimed pervaded space and time. However, these theories used these unobservable descriptions of reality to achieve incredible success in prediction and explanation. And science is chock full of success stories just like that.
Wouldn't it seem like an utter miracle if these theories achieved so much success by accident?

Is the success of science simply miraculous?
The argument that makes this intuition a bit more precise is called the no miracles argument. It was posed using this charming language by Hilary Putnam (1975). We will formulate it as follows.
No Miracles Argument
- Success. Our best scientific theories enjoy a great deal of success, even when they describes unobservable aspects of the world.
- Best Explanation. The best explanation of such extreme success is that the descriptions of science are true, or at least approximately true.
- IBE.We ought to infer to the best explanation.
- Conclusion. Therefore, our best scientific descriptions are true, or at least approximately true.
We have already discussed how science is successful. Let's talk a little bit about what inference to the best explanation is supposed to be like.
Consider the following scenario. You come home late one the evening, and are really looking forward to a pizza that you had leftover in the fridge. But upon arrival, you find to your horror that the pizza box is empty, and that your friend is sprawled out on the couch asleep with greasy pizza hands.

Evidence to support your inference: a pizza box.
What happened to the pizza? There are lots of explanations. Maybe you ate it and forgot about it. Maybe it spontaneously combusted and covered your friend's hands in pizza grease. Maybe a pizza ninja stole it and tried to frame your friend.
However, the best explanation of the situation is probably that your friend shamelessly devoured your pizza. Good reasoning demands that we to infer to this conclusion.
The idea of the No Miracles Argument is that there is a similar situation with science. Of the many possible explanations of its success, the best explanation is approximate truth. So, the argument goes, good reasoning demands that we infer to this conclusion.
More Careful Scientific Realism
Premises 2-3 of the no miracles argument are equivalent to the assumption that a scientific theory is successful only if it is true.
That may seem plausible at first. But if you think about it for more than 2 seconds, there seem to be obvious counterexamples. For example, Newtonian gravity had a number of success in explaining the unobservable structure of the solar system, including the existence of planets before they were observed. But Newtonian gravity is false, makes incorrect predictions, and has been superseded by Einstein's curved spacetime theory of General Relativity.

A curved spacetime of general relativity
Thus, Newtonian gravity seems to provide a simple counterexample to simple No Miracles claim that Success implies Truth.
But scientific realism is not so easily destroyed. We just need to adopt a more careful kind of scientific realism. Here are two ways to do this; some realists adopt both, while others adopt just one or the other.
Preservative Realism
Scientific theories are not indivisible blobs. Theories have parts. For example, part of evolutionary theory is captured by the phenomenon of natural selection. Another part is captured by sexual selection.
We can replace the "Success" premise of the No Miracles Argument above with one that better captures the fact that theories have parts.
1PS. Preservative Success. Parts of our best scientific theories produce a great deal of success, even when they describes unobservable aspects of the world.
Preservative realists then argue for the conclusion that the success-producing parts our best scientific descriptions are true, or at least approximately true. You should verify that this conclusion is a valid consequence of the No Miracles argument with 1PS replacing 1.
So, for example, Newtonian gravity is approximately true in its predictions, even if it is not strictly true.
Can you give any other examples of how this might work in practice?

The view that the successful parts of a scientific theory are what we should consider to be approximately true is called preservative realism, sometimes also referred to as the "divide and conquer" response. It's kind of like having a puzzle, in which we're keeping the pieces that provide a successful description, discarding those that don't, and sometimes adding more pieces when necessary.
Structural Realism
Another approach to realism is to notice that theories deal not only with objects, like a light wave, but also with more abstract structures, like the equations governing the behaviour of light.
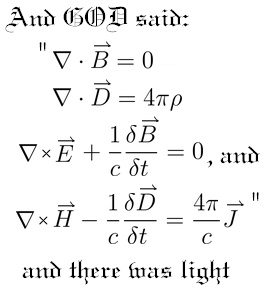
Maxwell's Equations are what define light waves in classical electromagnetism.
Suppose that we think of each theory as being separable into its concrete parts and abstract structural parts. Then we can reformulate the first premise of the No Miracles Argument as follows.
1SS. Structural Success. The structural parts of our best scientific theories enjoy a great deal of success, even when they describes unobservable aspects of the world.
This adjustment leads to a view known as structural realism, which counsels that it is the structural aspects of our best scientific theories are true, or at least approximately true. (You should verify that this conclusion is a valid consequence of the No Miracles Argument with 1SS replacing 1.
An outgrowth of an old debate
Scientific realism is about the the unobservable claims of science, nothing more and nothing less. However, it is a variant of a much older debate about the reality of the external world.
Could the world be no more than a dream? Could it be an elaborate illusion created by a powerful deceiving demon? Is there anything out there at all? These are the questions of external world realism, studied most famously by Descartes.

In his first meditation Descartes postulated that reality might be an illusion created by a dream or by some malicious demon
In a charming and readable little discussion called Meditations on First Philosophy, Descartes argued that yes, you can be absolutely sure that the external world is real. However, some of his critics disagreed. For example, the Irish philosopher Bishop Berkeley argued that there is no "external" world at all; reality consists exclusively of minds and ideas. This view is called idealism.
Both of these views are in a sense a little extreme. They also ignore the special role that science plays in providing us with knowldge about reality. For this reason I would advice you to assume the world of everyday objects is real, at least to some degree of plausibility. After all, for practical purposes, we all certainly behave that way. And by assuming everyday objects are real, we make way for the more interesting discussion of scientific realism, of realism about the unobservables of science.