Notes on Time Travel and Global Constraints
Bryan W. Roberts
University of Southern California
ARLT-100: Einstein's Spacetime Revolution
Background Reading: Arntzenius and Maudlin
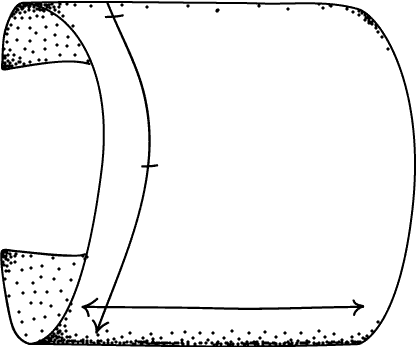
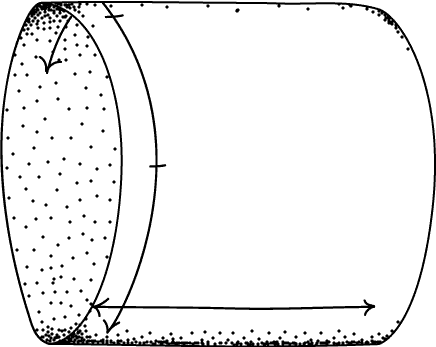
Consider a world with closed timelike curves, i.e., a time travel world. A simple toy model for this involves rolling up a chunk of spacetime along the timelike direction.



In such a world, you might consider killing your past self. However, you will not succeed if consistency is to be maintained!

So, you cannot do anything that you want in a time travel world. What can you do? Here are some examples.
You can carry out the action of inverting a grayscale photo, and then letting the photo go back around to its previous self in time. Question: when you do this, what does the photo that you invert a photo of?
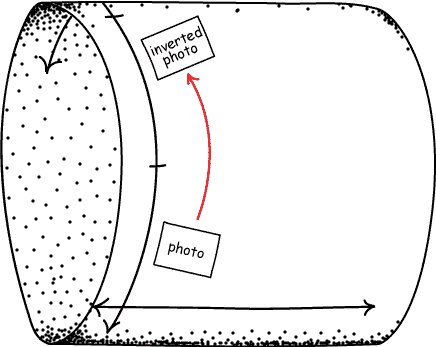






There is only one option. In order to maintain consistency, it must be a photo that is invariant under inversion.
More general actions are allowed in our time travel setup. However, the kinds of initial conditions that you can apply the action to are severely restricted!




It is possible to invert a color photograph in our time travel setup as well. But, there is only one photo that will be allowed.




More general kinds of changes can occur in our time travel setup. Artzenius and Maudlin suggest we think of this as a continuous change of any quantity we like. Under certain conditions, these continuous changes are possible, like the "smooth change" of a body's temperature within some fixed interval (say, from 0F to 212F).

We can "spin" an object as well, but we can only spin things at a very particular rate. Use the diagram above to try to imagine how a spinning object might evolve on a closed timelike curve.
Take Minkowski spacetime, and cut two slits in it. Identify the upper lip of the top slit with the lower lip of the bottom, and vice versa. The result is called "Duetsche-Politzer spacetime," named for the two physicists who first considered it.
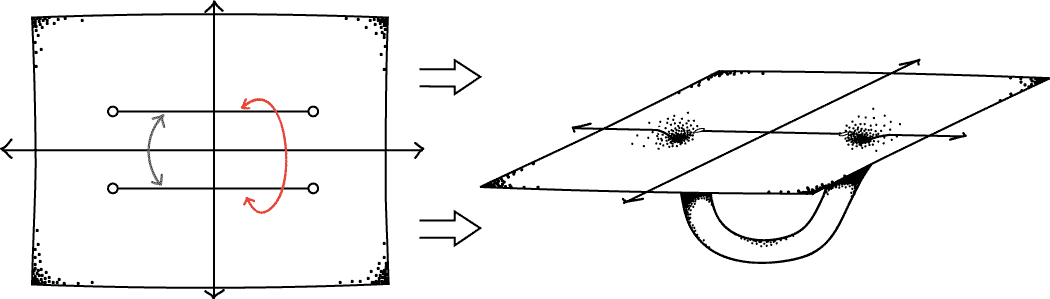
This universe is just almost everywhere just like Minkowski spacetime! The exception is one little region where there is a "handle" containing a closed timelike curve. We call such a region a "time travel region."
Suppose we are in some region that looks just like Minkowski spacetime. Can we know if there is a time travel region to our future? That is, can we know if we are in Deutsche-Politzer spacetime as opposed to Minkowski spacetime? The answer is yes, sometimes. There are certain things we can do in Minkowski spacetime that we cannot do in Duetsche-Politzer spacetime.
Example: we can spin an object at any speed we like in Minkowski spacetime (so long as it is less than the speed of light). But in Duetsche-Politzer spacetime, we cannot spin an object in an way we like. If we send a spinning object into the time travel region, it must spin in such a way that it maintains consistency in the time travel region. That is, there are certain rates of spinning that are not allowed.
Question: What would this be like? You would find yourself trying to spin a top, and finding that for no apparent reason, only certain discrete rates of spinning were possible, for no apparent reason given the past history of the top.
Read the more exotic example of how to test for this in the reading. Try to think of your own way to test if there is a time travel region in your future.

The central complaint is that a global constraint amounts to some kind of "divine harmony" between the behavior of the system on a global scale, and the local behavior of matter in a small region of spacetime. How might one respond to this complaint? What are the counter-replies? Consider each of them carefully, and see if you can formulate your own view on this matter.
Response 1. There other places where we encounter global constraints in general relativity, where they are not implausible. (Can you think of examples? Can you think of a counter to this response?)
Response 2. We encounter global constraints in other theories, like electromagnetism, and this is not implausible. (Counter-response: these seem to be of a very different character from the case of time travel universes.)
Response 3. Time travel regions just involve "self-interaction." This is just like regular interactions, and although it appears strange because the interaction is with one's self, it is not implausible. (Counter-response?)
Response 4. Constraints are just contingent coincidences. We don't need to explain them, any more than we need to explain why the moon has the specific mass that it does -- it just happens to, that's all. (Counter-response?)