What's in a cause?

In Aristotle's time, one had to be careful how one used the word "cause" (αιτíα), because there were four different concepts associated with that word. Aristotle famously associated these concepts with different facts about a statue. It was a bit confusing, as Aristotle himself freely admitted.

We will do not have to deal with that confusion today. Modern discussions of causation are almost exclusively about what Aristotle called "material" causes, as in, "the statue's shape was caused by the sculptor's chisel". Instead, we are faced with the more difficulty question of determining what (if anything) counts as a cause.

There has been a noble search for causes among philosophers spanning hundreds of years. One common sentiment is that, whatever the nature of causes, they seem to play an important role in science.

"All alterations take place in conformity with the law of the connection of cause and effect"; "Everything that happens, that is, begins to be, presupposes something upon which it follows according to a rule." — Kant, Critique of Pure Reason

"The law of causation, the recognition of which is the main pillar of inductive science, is but the familiar truth that invariability of succession is found by observation to obtain between every fact in nature and some other fact which has preceeded it, independently of all considerations" — Mill, System of Logic

But is what Mills says correct? Is causation really the "main pillar of inductive science"?

Causal Fundamentalism

Mill takes causation to be absolutely fundamental to the scientific study of the world. This view can be put more generally as follows.

There are some indications that Mill might be right. For example, the motto of the world's centre for social sciences is "To Know the Causes of Things". And just look at all these articles in the physics repository arXiv.org that have "cause" in the title!

If causal fundamentalism is right, then it suggests that we need to understand the character and rules underlying causal behaviour. Many approaches to understanding causation have been pursued. We shall discuss three of them.

Causation 1: Regularity Accounts

Our first account of causation was stated explicitly by Hume, in his Enquiry concerning Human Understanding. Hume wrote that, "We may define a cause to be an object followed by another, and where all the objects, similar to the first, are followed by objects similar to the second."

Regularity account of causation. C causes E if and only if the occurrence of C tends to imply the occurrence of C and E.

Since "conjunction" means sticking two propositions together with "and", this property is often referred to as constant conjunction — when C occurs, it is constantly conjoined with E.

This account does get a number of things right. For example, drinking poison causes death:

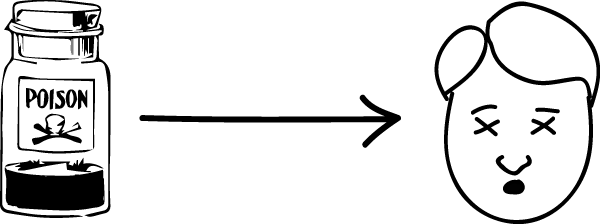
This can be characterised by the fact that drinking poison tends to imply that the drinking is accompanied by death. Similarly, fire causes smoke:

However,there are at least for kinds of cases in which the regularity account of causation dramatically fails.

1. The regularity account describes many things as causally related that are better described as mere accidents. For example, a decrease in pirate population has been regularly accompanied by an increase in average global temperature. But these two things surely are not causally related.

2. The regularity account often describes events as cause and effect when there is actually a different common cause of both. For example, smoke-stained teeth tends to be accompanied by lung cancer. However, yellow teeth is not itself a cause of cancer.

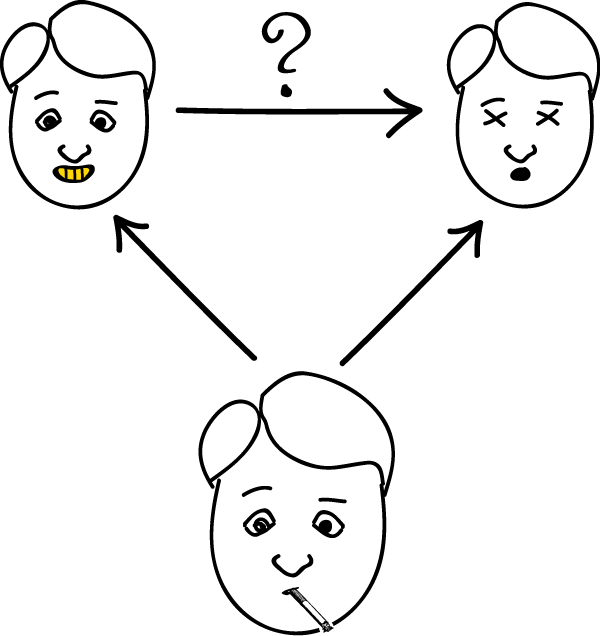
Rather, it is the smoking that tends to be a common cause of both.

3. The regularity account easily mixes up cause and effect. For example, since lung cancer is almost exclusively accompanied by inhaling cigarette smoke, the regularity account deems that lung cancer causes the inhaling of cigarette smoke. That is, it gets the causal direction wrong.

4. Finally, the regularity account seems to incorrectly treat preemptive backups that don't themselves cause anything to happen, but are there waiting as a backup in case a planned cause doesn't occur. For example, consider a firing squad in which only one soldier fires, but the others stand ready to deliver a coup de grace in case the first soldier misses.

Only the soldier who fires may be the actual cause the prisoner's death. However, the accompanying soldiers would seem to be labelled as causes on this account as well, since their presence tends to be accompanied by a dead prisoner.

Adequacy of an Account of Causation

Some of the problems with the regularity account can be put in terms of a criterion of adequacy to help guide our search. A decent account of causation should:

It has often been suggested that one can guarantee 2 by simply requiring causes to occur before effects in time. This may often help, but there are many cases in physics in which it doesn't work.

For example, in Newtonian gravitation, a change in the shape or position of a massive object like the sun leads to an instantaneous change in the force of gravity exerted on the Earth. The sun certainly seems to be the cause of the gravitational force. But it does not occur before its effect in time.

Another example of causes not preceding effects is known as state reduction in quantum mechanics. Particles in quantum mechanics are typically in a state known as entanglement, in which their behaviour is correlated no matter how far apart they are in space.

So, although it may be intuitively reasonable to place causes before effects, it's not clear that Nature requires any such thing.

Causation 2: Statistical Accounts

Statistical accounts of causation pick up on the fact that our descriptions of the world are typically probabilistic, from the behaviour of social sciences to the behaviour of quantum particles. So, it would be advantageous to describe causation in terms of probability.

A first, naïve attempt at a statistical account of causation is to say that a causal influence is one that increases the probability of an effect. More precisely, we have the following.

Naïve statistical account of causation. C has a causal influence on E if and only if Pr(E|C)>Pr(E).

A neat aspect of this account is that it allows us to more naturally treat situations in which there are multiple causal effects. For example, the runners in a relay race may all have an influence on the probability that their team wins the race. No single runner is a complete cause, but each contributes to the probability.

Unfortunately, this account fails in all the same ways as the previous one. If you think about it for a minute (and you should!), you will quickly see that the naïve statistical account in all the same ways as the regularity account.

1. It fails to distinguish between genuinely causal relationships and mere accidents.
2. It fails to distinguish between causes and effects.
3. It fails to distinguish causes and effects from a common cause.
4. It fails to distinguish genuine causes from "preemptive backups."

However, probability is a powerful language, and more powerful accounts have been given. Suppose we begin by describing causes and effects in terms of directed graphs like the following, where effects are "downstream" of causes in the graph.

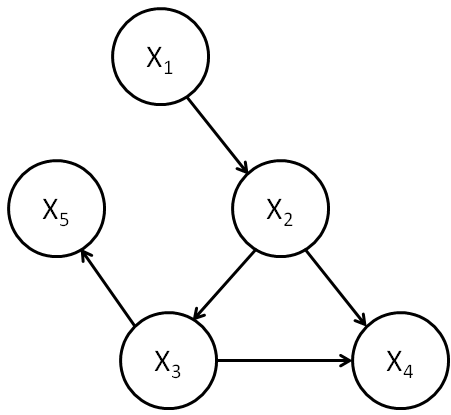
These kinds of causal graphs tend to satisfy certain plausible conditions about probabilities. Spirtes, Glymour and Scheines (SGS) were among the first to notice this in the early 90's, and their work culminated in a well-known treatment of causation called Causation, Prediction and Search. Their main results were a series of arguments showing that three simple axioms relating probabilities to causal graphs capture a great deal of causal scenarios in the natural and social sciences.

SGS called these axioms the causal Markov condition, the causal minimality condition, and the faithfulness condition. Although their precise definitions will take this discussion to far afield, you can read more about these remarkable axioms here.

Since such an axiom system relating probability to directed graphs is often called a Bayes net, it is referred to as:

The Bayes net account of causation. A set of events are causally related in the sense described by a directed graph if and only if the probabilities describing those events satisfy a set of axioms, such as the SGS axioms.

This powerful system does appear to distinguish causes from mere accidents, and has no trouble with preemptive backups and with most common causes.

However, the Bayes net approach is time directed, and must be in order to reliably distinguish typical causes from effects. As a consequence, it does not allow causes and effects that happen at the same time, such as the effect of Newtonian gravitation or of quantum state reduction described in the previous section. The Bayes net approach thus fails to identify such events as either directly causally related or related by a common cause.

Causation 3: Counterfactual Accounts

Counterfactual accounts of causation involve a simple addition to the regularity account that fixes many of its problems. The key move is to consider what might have happened instead of what actually did happen. The description of "what might have happened but didn't" is known as a counterfactual — it runs counter to the facts, but is still a sensible description.

Counterfactual account of causation. C causes E if and only if 1) C implies C and E, and 2) if C had not occurred, then E would not have occurred.

Many of the problems with the regularity account are immediately fixed with this addition.

1. Mere accidents are no longer a problem. Consider the case of decreasing pirate population vs global temperature. We can now simply notice that if the pirate population had not decreased, then global temperatures would have still increased. So, pirate population is not causally related to global temperature.

2. Common causes appear to be correctly described. For consider again the relationship between yellow teeth and lung cancer. Had you not had yellow teeth, for example because you had no teeth at all, or bleached them regularly, the cancer would have still occurred. So, yellow teeth are not cause of cancer.

On the other hand, if you had not inhaled cigarette smoke, then you almost certainly would not have gotten lung cancer. So, cigarette smoke would still be considered a cause of lung cancer, as expected.

3. Causes and effects can still be mixed up, unless one introduces the explicit condition that causes preceed effects. For example, consider the hypothesis that lung cancer causes smoking. If you had not had lung cancer, then the smoking would not have occurred either. Thus, it seems that the counterfactual account also (incorrectly) deems that lung cancer causes smoking.

4. Founders on preemptive backups. Counterfactual accounts tend to fail dramatically in dealing with preemptive backups.

For example, consider again the firing squad discussed above. The first soldier shoots and kills the prisoner. The second soldier stands by to deliver the coup de grace in case the first soldier misses. Question: does the first soldier cause the death of the prisoner?

Not according to the counterfactual account set out above. For suppose (counterfactually) that the soldier had not fired the gun. The prisoner would still have died by the hand of the second soldier. So, the first soldier did not cause the death according to the counterfactual account.

Alternatives

The table below summarises how these approaches to causation fared by our criteria of adequacy, according to the discussion above. The Bayes Nets approach is stated to fail at least because of its treatment of quantum mechanics.

There is a thriving research programme that seeks alternatives to these accounts. You can read about a number of sophisticated probabilistic accounts, counterfactual accounts, manipulability accounts, and causal process accounts, which we do not have time to survey here. But all of them tend to grapple with the four concerns identified above.

Against Causal Fundamentalism

Bertrand Russell noticed that, although the concepts of "cause" and "effect" are often used in ordinary language, they do not appear in scientific textbooks.

Why would that be? Here is what Russell said.

All philosophers, of every school, imagine that causation is one of the fundamental axioms or postulates of science, yet, oddly enough, in advanced sciences such as gravitational astronomy, the word 'cause' never appears... To me, it seems that... the reason why physics has ceased to look for causes is that, in fact, there are no such things. The law of causality, I believe, like much that passes muster among philosophers, is a relic of a bygone age, surviving, like the monarchy, only because it is erroneously supposed to do no harm.

This is the kind of world that John Norton envisages as well: a beautiful world full of lawlike behaviour, but no causes.

Causation, according to Norton, is just "folk science", in that we use it as a convenient shorthand, but causation does not itself correspond to any underlying physical reality.

Norton states his negative thesis as the claim,

"that the concepts of cause and effect are not the fundamental concepts of our science and that science is not governed by a law or principle of causality."

Why think that we will never discover the fundamental laws of causation? The first reason is that we have been trying and failing for hundreds of years. There is no shortage of proposals:

• Regularity accounts
• Statistical accounts
• Counterfactual accounts
• Manipulability accounts
• Causal process accounts
  :
  :

None of them are completely agreed upon, and all of them have their problem. Norton takes this to be an indicator that causal fundamentalism is false, and that Nature is not governed by any law of cause and effect. As with the pilot that regularly crashes, it would seem foolish to trust in the future success of causation.

Norton poses the sharpest argument for his skepticism as a dilemma, which is the following.

However, there is a positive side to Norton's account as well, which is that causation often provides a helpful heuristic language. For example, consider a simple mechanical description such as, "Toy car bumps into domino array, which releases a toy card down a slide, which knocks a ball down a ramp, ...." all of which ends with the firing of a paint gun, as in the music video below by OK Go.

This complex description of events might be more simply described by the shorthand, "The toy car caused the firing of the paint gun". But this description is just folks science, which, like a folk language, tends to be a mere approximation of what is actually going on. A more correct basic description would be the more complex mechanical one that describes how each of the steps occurs.

Norton's Dome

After making this argument, Norton hoped to further illustrate the futility of the project using a simple Newtonian mechanical system as an example. This infamous example is now known as Norton's dome, and has become a topic of considerable discussion in its own right.

If causal fundamentalism stands any chance at all, Norton suggested, it should always be possible to give a causal account of a system described by F=ma, Newton's second law. So, Norton sets up a particular dome-like surface in which the curvature becomes very sharp at the apex, and then considers what happens to a mass placed at rest exactly at the apex.

You can read about the details of Norton's calculation here if you are interested in the physics. But the remarkable result is that Norton's dome is deeply indeterministic: the ball might sit at the apex for all of time, but it is equally compatible with Newton's law to have the ball begin spontaneously rolling down at any arbitrary moment in time.

Animation Credit: John D. Norton

Norton's conclusion is that, since even simple Newtonian mechanics admits acausal behaviour, the search for a fundamental law of causation is certainly doomed.

Few readers have drawn this conclusion from Norton's example. Instead, much of the focus has been on the strange features of Norton's dome that allow for this indeterministic behaviour. For example, the curvature of the dome is not just very large at the top, but infinite at the apex. So, it would not only be impractical for a careful dome builder to create such a dome, it would be impossible to create using straight cuts in a finite amount of time.

However, just because Norton's dome is impossible to create does not mean that it is impossible. As a result, most considerations of Norton's dome have turned to the question of what counts as a reasonable description of a physical system, and whether any reasonable requirements are enough to ensure determinism in Newtonian mechanics.