Prolegomena
One Sunday morning in Seattle, the rainy little city near where I grew up, a pair of newly weds sat down to have breakfast together.
They drank their coffee. They ate their toast. They shared the newspaper. It was their normal Sunday routine. Many of us have such a routine: perhaps you go for a run, chat on the phone with a family member, prepare yourself for work the next day, or just loaf around the internet. Imagine doing those things, just like this couple was doing. It was a perfectly ordinary Sunday morning at the dining table.

Except for one thing — this wasn't their dining table. It wasn't even their home. When you look a little closer, you notice cameras on the walls, little microphones on their clothes, and heartrate monitors strapped to their chests. Although the room looks like an apartment, it isn't. It's a laboratory. This wasn't just any couple, but one that was randomly selected from among a group of volunteers studied in Dr. John Gottman's lab at the University of Washington, affectionately known as the Love Lab.

Dr. Gottman brought thousands of couples into his Love Lab and studied their every move. His aim was what many would have called an impossible task: the scientific study of love.
The poets among us sometimes find such things outlandish. If there is anything that lies beyond the limits of what science can effectively study, surely love is one of those things. Isn't it? But let me just mention a few of the things that Dr. Gottman has learned.
- When couples separate. Dr. Gottman's model predicts a couple's separation with 91% accuracy. Will a couple stay together, or go their separate ways? He could tell which one it would be by listening to them talk for as little as 5min.
- When communication helps. When a couple has a discussion in response to a conflict, Gottman's model can observe them for three minutes and determine whether the discussion will resolve the conflict, or whether the conflict will persist or possibly get worse. With 96% accuracy.
- The facts of love. Gottman found a number of concrete facts about love, such as the determining factor in relationship satisfaction by 70% is the quality of the couple's friendship. It's the same for men as it is for women.
In many ways, Dr. Gottman did what once seemed impossible: he made love a matter of science. Imagine! If there was anything that the story books and poets would have assured us is safely outside the icy clutches of scientists and philosophers, surely love would be. But it isn't. The poet E.E. Cummings once lamented, "Oh sweet spontaneous earth, how often have the doting fingers of prurient philosophers pinched and poked thee, has the naughty thumb of science prodded thy beauty". It turns out that not even love has escaped our scientific clutches.
If even love is a matter of science, then are there any limits to science at all?
I'm going to try to make this question a little clearer. The plan:
- Discuss some examples of limits
- Distinguish between two different kinds of limits
- Use this distinction to clarify some limits in physics
- Identify a sort of limit that it appears we will never overcome.
We will be discussing some examples of limits in science, and by reflecting on their general character. We'll consider some limits that seem impossible but can actually be overcome, and other limits that once seemed surmountable but are actually impossible. How can we know the limits of science? It is a startling consequence of the nature of science itself. Part of the beauty of science is not just that it produces knowledge, but that it produces doubt. Indeed, the methods of science are are just as apt at determining what we do not (or cannot) know.
Some Limits
There are certainly some limits to science.
For example, next week we can broadcast a football match on television all around the country. But we can't broadcast the match all the way to the Andromeda galaxy by next week. Our television signal travels at the speed of light. And the Andromeda galaxy is around 2.5 million light years away.
In fact, the very first television transmissions haven't even left our own galaxy yet. Those signals have only been hurtling away from Earth for the past 85 years. That puts them just around the outskirts of the little clump of stars we live in, called the Star Cluster.

The expanding television shell on the star cluster scale.
But it takes 27,000 light years to get to the edge of the galaxy. Those first television shows will have to travel another 26,915 light years to the edge of the galaxy, and millions more years beyond that before reaching Andromeda.

The expanding television shell on the galactic scale.
There are other more wordly limits. For example, we don't know very much about the deep sea, due to the physical limitations on survival at crushing deep-sea pressures, which can be as much as 1000 times atmospheric pressure.

There are also intellectual limits. For example, in the 20th century, a computer was limited in its ability to play chess better than the world's top grand-masters. And humans could perform complex tasks much more effectively than robots, which were generally restricted to simple manual labor tasks such as the assembly of a car.
Famously, both of these limits have been overcome, with the development of chess-playing computers that often defeat grand masters, and robotic self-driving cars that are able to drive better than humans can.

You might be wondering at this point if there are subjects that are untouchable by science. All the limits I've discussed so far are limits from within scientific practice. But are there areas to which scientific practice cannot even be applied?
This is really just another part of the same question. Like the scientific analysis of love, it seems that such subjects are often just limits waiting to be overcome. Sometimes limits aren't really limits at all, but just artificial shortcomings of our current human abilities! However, there may be other limits that will probably never be overcome, no matter what we do.
Human Limits vs Hard Limits
These sorts of cases suggest we can draw a helpful distinction between human limits and hard limits. Human limits are artificial and often temporary limitations that we simply don't have the cleverness or resources to overcome. Hard limits will probably never be overcome.
I would like to point out that an important activity in science consists in identifying and distinguishing between human limits and hard limits. It it is often difficult to know that something is a limit at all. And when we do know we have a limit, it's often very hard to know if it's a human limit or a hard limit.
Many subjects that were once identified as being 'outside of science' turned out to just be the subject of human limits. For example, it was once the case that the only observations we could make about the cosmos came from the light of distant stars that is visible by the human eye. We have come a long way since then.
For example, Galileo's telescope fundamentally changed our ability to know about the universe. More recently, cosmic rays, and now gravity waves, are again providing us with fundamentally new ways to understand the cosmos. In science, human limits are being overcome all the time. It's a dangerous bet to say something is always outside the scope of science.
Let's explore some examples to try to understand what this practice is like.
Human Limits: Zeno's "Paradox"
It's often very difficult to distinguish whether a limit is human or hard. Many brilliant thinkers have confused one for the other.
For example, the pre-Socratic Greek philosopher Zeno of Elea was concerned with certain limits of motion now known as Zeno's paradoxes. Zeno thought these paradoxes illustrated hard limits that could never be overcome.
In fact Zeno's paradoxes reflect a human limit that has since been overcome. The problem was not that Zeno lacked material resources, but that he lacked mathematical and conceptual resources that allow us to overcome the paradox today. Here's how.
Zeno Paradox 1: Achilles and the Tortoise
Achilles is a lightning fast runner, while the tortoise is very slow. And yet, when the tortoise gets a head start, it seems Achilles can never overtake the tortoise in a race. For Achilles will first have to run to the tortoise's starting point; meanwhile, the tortoise will have moved ahead. So Achilles must run to the tortoise's new location; meanwhile the tortoise will have moved ahead again. And it seems that Achilles will always be stuck in this situation.

So, it seems Achilles can never overtake the tortoise.
Zeno Paradox 2: The Dichotomy
This version of the paradox says, forget about the tortoise. Achilles can't even make it to the first flag! For in order to do so, he would have to first go half thte distance. Then he would have to go half that distance (or 1/4 of the total). Then half that distance (1/8 of the total). And so on ad infinitum. Since there are infinitely many "halves" for Achilles to cross, he can never make it to the first flag.

This reasoning has an extreme consequence. Just ask whether you can move from one point in space to any other point at all. So, Achilles cannot move at all. Another way to put this is in terms of a regressive version of the problem. Here we imagine what it would look like if Achilles did arrive at the flagpole, and then play his trajectory back in reverse.

In order to reach the flag, Achilles would have to complete the last half of the race. But before he can do that, he must complete the 1/4 of the race just prior. And before that he must complete 1/8 of the race prior, and so on. There is no end to what he must do before completing the race — indeed, it looks like Achilles can never get started in the first place!
A Zeno-Like Paradox: Thompson's Lamp
If you've puzzled over Zeno's paradoxes before, you may not have seen a related "paradox" known as Thompson's Lamp.
Suppose that we switch the lamp off after 1/2 a minute, then on after 1/4 a minute, then off after 1/8 a minute, on after 1/16, and so on ad infinitum. By the same limiting argument used to solve Zeno's paradoxes of Achilles and Dichotomy, we know that this procedure will be complete after a single minute has passed (since 1 is the limit of the infinite sum, 1/2+1/4+1/8+1/16+...).
At the end of the process, is the lamp on or off?
Some have claimed it could be neither. For each moment at which the lamp is on is followed by an action that turns the lamp off. And each moment at which the lamp is off is followed by an action that turns the lamp on. So, the argument goes, it can neither be on nor off!
Overcoming Zeno's Paradoxes
Much of the puzzle of Zeno's paradoxes can be overcome by separating two distinct concepts: the concept of completing a task vs. completing the final step of a task.
The tasks that Achilles sets out on are initially puzzling because they lack a final step. However, there is no logical requirement that binds us to believe that every task that we complete has a final step. In other words, infinitely many intervals does not imply an infinite total length.
Zeno merely lacked the conceptual resources to understand how a task with no final step could be completed. In fact, this was not really understood until the nineteenth century, when mathematicians discovered a precise sense in which an infinite sum could converge to a finite number. In the case of Zeno, this indicated the precise sense in which the following sequence of sums approaches a finite number: 1.
1/2
1/2 + 1/4
1/2 + 1/4 + 1/8
1/4 + 1/4 + 1/8 + 1/16
:
:

There is a rich theory of limits underlying this fact, which you can learn more about in the next chapter. You will learn about more exotic examples like Thompson's Lamp in later chapters.
In sum, the Zeno-style paradoxes mistake a human limit for a hard limit. And as soon as we had the conceptual resources available, this limit was overcome, and Zeno's paradoxes were resolved.
Einstein's struggle with hard limits
There is a story about how Albert Einstein struggled with both human and hard limits throughout his career. The first one you might have heard of before has to do with what happens when you chase a light beam. The other ones are a little bit more subtle. They have to do with how to interpret the situation when the laws of nature break down.

Chasing the Light Beam
One of Einstein's first encounters with a limit happened when he was 16 years old. At the time he was just a boy preparing for the entrance exams to the Swiss Federal Polytechnic University in Zürich. Although he did well in math and physics on his entrance exams, his general marks were not good enough to enter, so did not attend the University in that year. Instead, he came up with the chasing a light beam experiment, one of the most famous thought-experiments in the history of physics.
A beam of light moves along at the unimaginably fast speed of about 300,000 kilometers per second, the speed of light in a vacuum.

A moving light ray. Image credit: John D. Norton
The speed of light is far, far beyond the paltry earthly speeds that humans have managed to achieve. The fastest speed that a human has ever traveled relative to Earth is 39,000 km/hr, the speed hit by the Apollo 10 astronauts on their descent to Earth. And that speed is only about 11km/s, or 1/30,000th the speed of light.

But is this only a human limit? What if we had all the resources imaginable available to us, including fancy spaceships and an arbitrarily large amount of fuel. Would it be possible to reach the speed of light?
To approach this question, Einstein imagined what would happen if he could catch up with that beam. Moving ever faster and faster, he imagined what would happen in the limit as he actually reached the speed of light. How would the light beam appear?
The answer, Einstein thought, was that it would appear frozen, though still oscillating in space.
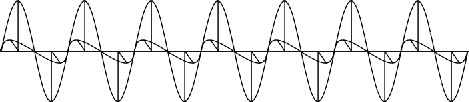
A "frozen" light ray. Image credit: John D. Norton
This idea seemed so absurd to Einstein that it led him to begin wondering if perhaps the speed of light acts as a universal limit on the motion of material bodies. Eleven years later in 1905, Einstein was finally able to prove that this postulate was correct. In formulating the theory of Special Relativity, he showed that material bodies traveling slower than light cannot accelerate to the speed of light or faster.
This fact about material bodies does not depend on our human resources or limitations. More than a hundred years after Einstein's discovery, all of our best physics still confirms that it is impossible for massive material bodies to move through empty spacetime faster than light. Einstein had discovered a hard limit.
This hard limit captures a fact of relativity: unlike what you may have heard, relativity is not about what's relative, but about what's absolute. The speed of light in a vacuum is an absolute quantity in this theory, and our limitation to speeds that are slower than light is absolute.
Black Holes
Nobody ever said that overcoming a limit was easy. We began, after all, by questioning whether science is limited in its ability to help us understand love. Our next limit has to do with something almost as difficult: the study of black holes.

Black holes occur when matter becomes dense beyond a critical point, for example when very large stars collapse. The gravitational field around such objects gets incredibly strong. It's so strong that nothing can escape --- not even light.
Einstein himself tried to argue that black holes cannot form, incorrectly. Part of Einstein's confusion was about a strange kind of limit that arises around the black hole, which is the event horizon.
The event horizon of a black hole is the point of no return. It's the line that if you cross you cannot return from. But it also has a number of strange properties.
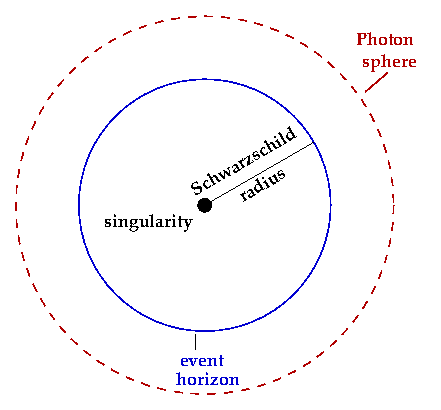
Suppose that I send my student out to investigate a black hole. My students are very committed to their studies. And this one decides to take the plunge, and actually see what it's like on the other side of the event horizon.
Safely back on earth, I watch my student with my telescope. What would I see as the student headed across the event horizon? I would not see the student cross. I would see the student get closer and closer to that horizon, the light that I receive from the student would become shifted more and more red, and I would only ever see the student get closer and closer. I would never see the student cross.
Crossing into a black hole looks at first like a hard limit from our perspective on earth. No matter how long I wait, I will never see the student cross. But it's not — it is a human limit!
It turns out the student, though sadly doomed, will feel no "bump" or any other strange phenomenon in crossing the event horizon. It's just smooth space. It only takes a moment to cross. So, the event horizon is not really a hard limit that lies outside the realm of what we can know. It only looks that way from a particular perspective. From the student's perspective, it looks perfectly natural.
This phenomenon has been nicely explained using fast-moving water, called a dumb hole.

In this example, we imagine that our student is a fish, that is going off the edge of a very tall waterfall. The water gets moving so fast that it eventually exceeds the speed of sound. There will be a particular place on that waterfall, called the "sound horizon", where that faster-than-sound motion will begin.
Now I (also a fish) am listening to my student cry out "Help!" as the student falls down the waterfall. What will I hear?
The sound waves from the students voice cannot come back up once they pass the sound horizon, since they're getting pulled away from me at faster than the speed of sound. So, I will never hear the student finish that cry. All that I will hear is "Heeeeeee...." and as the sound wave gets out, it will get "bass-shifted" to an ever-lower pitch.

Like the black hole, this is only a matter of perspective. It does not mean that I cannot know what it's like to go inside a black hole. The student, of course, notices no bump in falling off the waterfall. Only a feeling of impending doom....
This kind of horizon effect confused Einstein for many years because he was using an overly restricted coordinate system. He finally came to understand this error during a correspondence with the mathematician Felix Klein. Now, far from doubting the existence of black holes, we have observed a large number of them!
In this sense, crossing into a black hole is a human limit. Black holes are far away from us, practically hard to get to, and we can't observe such crossings from our current vantage point. But in principle it is possible for humans to know what is on the other side. Somebody, perhaps some unlucky human may even find out!
On the other hand, exiting a black hole once you've entered appears to be a hard limit. It is not just impossible because we don't have enough fuel for our rocket ships. The geometry of spacetime is such that every possible future outcome leads to the centre of the black hole. There is no trajectory that escapes it.

However, even this limit is not so clear. Black holes are an area of active research. In particular, it is now widely believed that every black hole is slowly evaporating, and will eventually disappear. If this is the case, then perhaps there is a possible way for something to escape a black hole after it completely evaporates. Researchers are actively working on how best to describe this kind of phenomenon. Thus, whether this particular limit is human or hard is a matter of active research!
Hard limits on what you can prove
I'd like to give just one more example of a limit in science, which has to do with what we can use mathematics to prove. If mathematics works at all, then there are some things that are true but not provable.
I don't mean this in any kind of vague sense. We actually have a theorem that proves it! It is called Gödel's incompleteness theorem. In that sense it is a hard limit. If what science does is seek to know things by proving them, then there will always be some things that can never be proved.
To get the rough idea of how one might prove something like that, consider the following sentence.
This sentence is not provable.
If mathematics works at all, then we must assume that it is consistent. So, we must assume that it is impossible to prove false things. So:
1. The sentence cannot be false.
If it were, then it would be provable, and so we could prove something false, and all of mathematics would be bunk. Therefore:
2. The sentence must be true!
But if the sentence is true, then it is an example of a sentence that is true but not proveable. That is the character of Gödel's theorem. Of course, a great deal of subtlety and sophistication is needed to make this mathematically precise. But you get the idea!
The limits of science are a matter of scientific study
What is remarkable about all of these examples of limits is that the limits are a matter of scientific study. To understand the limits of science, there is no better tool than science itself.
- Limits on the study of human relationships.
- Limits on the transmission of data like television signals.
- Limits on human travel, such as to deep-sea regions.
- Limits on the tasks a computer can carry out.
- Limits on one's ability to move.
- Limits on tasks like the turning on/off of a lamp.
- Limits on the speed of matter and light.
- Limits on what you can see from outside a black hole, or hear from outside a dumb hole.
- Limits on what you can do from within a black hole.
- Limits on what you can prove.
Many of these might have been said at one time to be unscientific, unknowable limits. On the contrary, we have come to understand the nature of many of these limits, and we have done so via the application of scientific practice.

