Wonder at the existence of the world
The questions of philosophy are sometimes so extraordinarily big that they just fill you with wonder. In a 1929 lecture on ethics at Cambridge, Ludwig Wittgenstein reports this as his greatest feeling of pleasure:
"[Suppose] I were to give you a lecture on the psychology of pleasure. What you would do then would be to try and recall some typical situation in which you always felt pleasure. ... And there, in my case, it always happens that the idea of one particular experience presents itself to me which is, in a sense, my experience par excellence .... I believe the best way of describing it is to say that when I have it I wonder at the existence of the world. And I am then inclined to use phrases such as 'how extraordinary that anything should exist' or 'how extraordinary that the world should exist.'" (Wittgenstein 1965 [c.1929-1930], p.7-8)

Ludwig Wittgenstein (1930)
This experience of wonder arises out of a famous question formulated by Leibniz, Why is there something rather than nothing? This is one of the big questions: it demands consideration of the nature of the universe as a whole. And it is a natural next question to ask if, on the basis of these considerations of the entire universe, we might uncover some evidence for or against the existence of a creator. That is the topic of today's discussion.
Contingency and Necessity
Modal Statements
The notion of a creator is often expressed using the concepts of possibility and necessity. So, we begin by introducing that distinction. Consider the fact that the Earth has a moon.

There is a sense in which this is accidental: a giant piece of rock became trapped in the Earth's gravitational field, probably after colliding into us, and became our moon sometime in the early years of the solar system. Of course, there could have been two moons around the Earth. After all, Mars has two moons, and Jupiter has dozens. It just happens to be the case that Earth only has one. In philosophy, this sort of accidental fact is called contingent: it could have been otherwise.
In contrast, the fact that every moon is subject to the laws of gravity is not contingent. It appears to hold no matter how many moons the Earth has, and under all physically possible circumstances. Philosophers call such a fact necessary: it could not have been otherwise. This distinction is sometimes explained in terms of 'possible worlds': a contingent proposition is true in some possible worlds, but not others; a necessary proposition is true in every possible world.

Newton's law of gravity
Note that the definitions of contingency and necessity both depend on what it means to be possible. Philosophers refer to statements about the possible and the necessary as modal statements. There are a variety of different senses in which something can be 'possible'. That is, there is a variety of modalities. Some are listed in the table below; you should try to think of some others!
| Modality | Meaning | Example |
|---|---|---|
| Logically possible | Possibly true in a given logic | Any non-contradictory statement of classical logic |
| Physically possible | Possible according to a given law of nature | A mass near Earth falls at a rate of 9.8 m/s2 |
| Legally possible | Permissible according to a given legal system | Standing on the left on a London Underground escalator |
| Morally possible | Permissible given some ethical system | An act that increases overall good (given utilitarianism) |
Necessary Beings and Gods
A necessary being is one whose existence is necessary, meaning that it exists in all possible worlds (given some definition of 'possible'). The concept of a necessary being has often been identified as a property of a god, although on different notions of what it means to be 'possible'. For example, Leibniz identified God as a logically necessary being. In contrast, William Craig has argued that God is rather a physically necessary being.
Being necessary is just one property that is often attributed to gods; some other properties often associated with gods are given below.
Properties often associated with gods
- Omniscient (all-knowing) being
- Omnipotent (all-powerful) being
- Perfectly good being
- Necessary being
- Punisher of wrong-doings
- Creator of the universe
- Designer of complex systems
- Eternal being (existing always)
- Omnipresent being (existing everywhere)
- Rewarder of good deeds
Most arguments for or against the existence of gods are in fact arguments for or against one or more of these properties. For example, Paley's Intelligent Design Argument is really an argument for a 'designer'. In contrast, Pascal's Wager is about the existence of a punisher of wrong-doings: Pascal argues that believing in a wrathful god is a safer bet than not believing in one, in particular if you happen to be wrong in your belief.
Although theologians often identify many of these properties with one and the same being, a separate argument is really needed to establish this. Otherwise, there is no guarantee that Paley's Designer and Pascal's Punisher are one and the same being. As a philosopher, you should think through not just whether any of these arguments are convincing, but also whether there is sufficient reason to believe they refer to a being that may be reasonably referred to as God.
In this discussion, we will focus only on the notion of a god as a necessary being and as a creator or designer of the universe. Our question is not exactly about whether a given religion's deity exists, but rather about whether either a necessary being or a creator exists.

Deities postulated by some major world religions
Avicenna on Necessary Beings
One argument for the existence of God in this sense begins by asserting that a necessary being must exist. A version of this argument was formulated by the Persian philosopher and polymath Ibn Sīnā, often known in English-translation as Avicenna, who lived from around 980 to 1037, during the Arabic Golden Age of 8th-13th centuries.
A typical expression of Avicenna's argument is the following.
"[A] being is either contingent or necessary. If it is necessary, then the point we sought to prove is established. If on the other hand it is contingent, that which is contingent cannot enter upon being except for some reason which sways the scales in favour of its being and against its not-being. If the reason is also contingent, there is then a chain of contingents linked one to the other, and there is no being at all; for this being which is the subject of our hypothesis cannot enter into being so long as it is not preceded by an infinite succession of beings, which is absurd. Therefore contingent beings end in a Necessary Being." (Ibn Sīnā's al-Risālat)

Persian philosopher and polymath Ibn Sīnā (Avicenna), ca. 970–1037
The central idea behind the argument is that there can be no infinite chain of contingent beings, each one causing the other. The idea was that it would be absurd to suppose that infinity exists in the natural world; indeed, this was a concern that extended for hundreds of years into the Scientific Revolution. Since an infinitude is impossible, Avicenna concluded that there can only be a finite chain of contingent beings, which includes in particular a first contingent being.
The next step is to assume that everything must have a 'reason' (or 'cause' or 'explanation'). So we can ask, what is the reason behind this first contingent being? It cannot be another contingent being, since this is the first. So, the reason must be a necessary being. This necessary being is then identified as God.
Infinite Chain
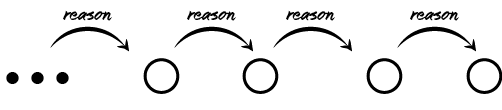
An infinite chain of contingent beings, each one the reason or cause for the next, is taken by Avicenna to be absurd.
Finite Chain

A finite chain of contingent beings is taken to begin with a 'first' contingent being c1. Since its cause cannot be contingent (since then it would not be 'first'), the cause n is taken to be necessary.
In the 17th century, Leibniz elevated Avicenna's assumption that everything must have a reason to the status of a philosophical axiom. Here is one of the ways Leibniz stated it in The Principles of Nature and Grace, Based on Reason:
Leibniz's Principle of Sufficient Reason: "Nothing takes place without a sufficient reason; in other words, that nothing occurs for which it would be impossible for someone who has enough knowledge of things to give a reason adequate to determine why the thing is as it is and not otherwise." (Leibniz 1714)
Thus, adopting the Principle of Sufficient Reason, Avicenna finds that the reason behind the first contingent being's existence must be a necessary being. Why call this being God, separate from the physical universe as a whole? For example, it would seem that one might identify the universe as a whole as the necessary being in Avicenna's argument. Craig (1991) finds this inadequate, arguing that a necessary being must also be 'eternal' in the sense of existing for an infinite amount of time. Since the universe appears to have a beginning, Craig finds that it would not suffice to describe the necessary being that appears in Avicenna's argument. Whether this is a reasonable argument, I leave up to you.
The Kalam Cosmological Argument
Overview
One may wonder about various aspects of Avicenna's argument. Why believe the Principle of Sufficient Reason? Why believe that there is not an infinite chain of contingent beings? A version of Avicenna's argument has been tightened and modernised by William Craig (1991), in an argument that he refers to as the Kalam Cosmological Argument. 'Kalam' here is short for 'Ilm al-Kalām' (literally, "since of discourse"), and commonly refers to discourse in support of a tenant of Islam. In this case, that tenant is the existence of a Necessary Being or God. It may be summarised as follows.
The Kalam Cosmological Argument
- Whatever exists has a cause (Principle of Sufficient Reason)
- The universe began to exist
- Therefore, the universe's beginning has a cause.
Craig assumes that the most reasonable way to understand the 'cause' of the universe's begin is in terms of a god, and thus takes this to be evidence that God exists.
The Kalam Cosmological Argument is valid: if the premises are true, then so is the conclusion. So, let's examine each of Craig's premises in turn.
Premise 1: The Principle of Sufficient Reason
Craig does not give a positive argument for the Principle of Sufficient Reason, writing only that
"[it] strikes me as relatively non-controversial. It is based on the metaphysical intuition that something cannot come out of nothing"
But why couldn't the Principle of Sufficient Reason be false? Especially in the case of the universe as a whole, it is certainly logically possible for it to fail, in that no contradiction arises in positing that something exists without a reason. So, it is hard to imagine Craig's comment convincing anyone who does not already believe the principle.
Instead, Craig responds to a critic of the principle, the physicist Paul Davies. In his book God and the New Physics, Davies argues that many questions formerly considered the providence of religion are now a matter of science. Davies suggests in particular that the creation of the universe is now a question of the science of cosmology, the study of the universe as a whole.
In this context, Davies suggests, there is no problem with uncaused phenomena, since according to quantum theory, particles regularly appear out of nowhere. Perhaps the universe is just like that.

The quantum vacuum allows particles to pop in and out of existence
Craig finds this argument misleading, since Davies later writes that this process actually consists in the "conversion of energy into material form". Thus, since the example is not analogous to the question of how the universe could begin out of nothing, Craig finds that the argument against the Principle of Sufficient Reason in this context fails.
Whether or not Craig is right about this, there remains the question of why we should think the Principle of Sufficient Reason is true in this context. But since Craig says nothing more about this, let us turn instead to his second premise.
Premise 2: The Universe Began to Exist
Craig gives two arguments that the universe must have a beginning, followed by claims that draw on science. In brief, they are the following.
Reason 2.1: Infinity is absurd
In the philosophy of mathematics, one often distinguishes between 'potential' and 'actual' infinity. A 'potential' infinity is like counting: you can potentially keep counting as high as you like, although and you will never finish. In particular, for each step in your counting, there is a further step that you would have the potential to carry out. In contrast, an example of an 'actually infinite' set is the totality of all integers. It is not just a potential ability to keep on going; it is truly infinite.
Craig argues that there is no actually infinite succession of contingent beings, because actual infinity is absurd, at least in the context of the physical world.
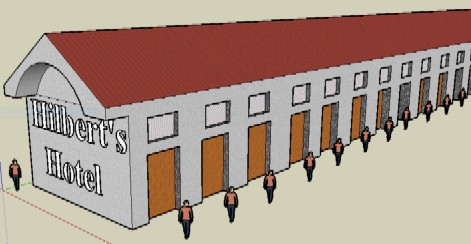
To establish this, Craig gives the following example. Consider a hotel with a countably infinite number of rooms. One night when the hotel is completely occupied, a traveller shows up and asks for a room. “No problem,” the receptionist replies, “there’s plenty of space!” The first occupant then moves to the second room, the second to the third room, the third to the fourth room, and so on all the way up. The result is a hotel that has gone from being completely occupied to having one room free, and the traveller can stay the night after all. This supertask was described in a 1924 lecture by David Hilbert, as reported by Gamow (1947).
According to Craig, this provides evidence that supertasks are physically impossible, although they may be logically possible.
Is this really evidence that actual infinity is impossible? One way of viewing Zeno's paradox is as evidence that, on the contrary, we carry out actually infinite successions of tasks all the time. For example, Zeno observed that in order for the runner Achilles to travel from between two points, he would have to travel half way, then half way again, and so on ad infinitum, as in the animation below.

Zeno himself argued from this example for the strange conclusion that motion is impossible, since it is impossible to traverse an infinite sequence of intervals. Alternatively, we can take this as evidence that, since we walk finite distances like this all the time, it is physically possible to traverse an infinite sequence. Such infinite tasks are known in philosophy as Supertasks.
More generally, if space is continuous, then every region of space — even the finite region inside this room — space contains an infinite number of points. If, as these arguments suggest, actual infinity is a normal part of the everyday world, then Craig's concern may not be so compelling.
Reason 2.2: No infinite successions
Craig's second argument an infinite succession of events could never physically occur. Whether or not an actual infinity exists, it would be impossible to create one by a succession of tasks, since every succession of tasks must have a beginning. Craig does not give an argument for this claim, but rather suggests that a succession without a beginning "seems to be absurd" (p.15).
Here too Zeno's paradox appears to present a difficulty. Imagine Achilles runs a distance from A to B. How could he do this? He would have had to go half way, and half the distance before that, and so on ad infinitum. This is illustrated below, and sometimes called the 'regressive' form of Zeno's paradox.

The task above has no beginning. This allows us once again to flip Craig's argument on its head: since we actually traverse distances like this all the time, it must be possible to carry out tasks with no beginning.
Reason 3: The big bang
Empirical evidence, together with the powerful mathematical reading of Einstein's theory of relativity, provides a compelling case that the universe has a finite past.

In fact, we can even see light from the very early universe, called the cosmic microwave background. It looks like this.

Craig gives an argument from this 'big bang' picture to the existence of a beginning for the universe. Our best cosmological evidence from physics seems to tell us that the universe has a beginning. He thus takes the big bang already to be sufficient evidence for his case.
A difficulty is that, in the actual models describing the big bang, it is not actually a point in space and time. It is instead an object known as a singularity, where the laws of physics break down. Although evidence for the big bang does indicate that the universe has a finite past, this does not imply it has a first moment. It is in this sense like the function y(x) = 1/x. You can approach it the big bang, the same way you can approach 0 along the function 1/x, but you will never actually get there, and there is no point corresponding to the beginning.

Thus, it is not so clear that the big bang provides the 'first cause' that Craig has in mind.
Quintin Smith argues that there is actually reason to think that the big bang provides evidence against gods. Science does not treat the big bang as a physical cause of any kind. But if we did so, then we would find an infinite amount of matter compressed into a single point. This point would consist in a total breakdown of the laws of physics. As a result, the universe would be totally indeterministic when one begins at this point. That means that there would be no guarantee that humans would exist. This contradicts the assumption that God must have created the universe in a way that guarantees humans will exist.
Is the universe finely tuned?
Just Six Numbers
Whether or not the Kalam Cosmological Argument succeeds, there is a related argument that is sometimes given that the universe must have a creator, similar to Paley's designer. There are a number of very specific facts about the universe such that, if they were just a little bit different, would not have allowed life in the universe to have occurred. Here are some examples; Sir Martin Rees gives many more in his book Just Six Numbers.
- Electrical force strength. If the strength of electrical forces were a little smaller, it would be impossible for creatures to grow larger than insects.
- Atomic nuclei binding strenght. If atomic nuclei were bound together a little less strongly, then the burning of stars would not have produced the chemical elements needed to create carbon-based life.
- Total matter in the universe. If there were a little more matter in the universe, then the universe would have collapsed long ago, before life on Earth cold have formed.
If these ideas are improbable, perhaps they require a designer in order to explain them.
Alternatively, one might wonder what probability means in this context. There isn't a succession or ensemble of universes that we have access to, the way that we flip a coin multiple times, which would allow us to say what the probability of this or that universe would be. Without the existence of multiple universes, it isn't clear what this notion of "improbable" really means, let alone whether it justifies the existence of gods.
How should we explain the universe?
From a scientific perspective, it is a remarkable cutting off of one's legs to ask a question as profound as, "Why is there something rather than nothing," and then simply assert that it must be because a god created the universe. It is analogous to asking the question, "Why is there lightening?" and then asserting that it is because the gods are angry.
By adopting this attitude, we may miss all of the fascinating science behind the question. Lightening is created by an incredible meteorological process of electrification in clouds. Perhaps there is a mechanism that transformed nothingness into the universe as we know it, too. It would have been a pity not to have known the electromagnetic explanation of lightening because we took gods to be enough of an explanation. Similarly, it be a pity not to further investigate the origin of the universe.