How does mathematics work?
Mathematics is a stunningly beautiful way to think. It contains some of the most wonderfully ornate constructions that that the human mind has ever managed to entertain.

A 4-dimensional cube, called a 'tesseract' or 'hypercube' - click to see it rotate (more)
Mathematics is also extremely useful. Galileo was so impressed by this that he was led to say that the universe is "written in the language of mathematics" in The Assayer (1623). But, unlike physics, biology and economics, useful mathematical theories are rarely rejected after they have been discovered, but instead tend to be generalised and deepened.
With such a remarkable body of knowledge, the philosopher is inevitably led to wonder, how does mathematics work? What sort of thing is mathematics about? What is it that gives it these incredible properties?

Some Natural Numbers featuring in Pascal's triangle
We're going to discuss these questions from the perspective of one of the most familiar bodies of mathematical knowledge, the natural numbers. But don't let the familiarity of these objects fool you: there is a sense in which understanding the natural numbers is as difficult and profound as understanding the entirety of mathematics.
Mathematics from natural numbers
The natural numbers, in short, are the counting numbers:
\(0, 1, 2, 3, 4, ...\)
Bertrand Russell, one of the most influential philosophers of the 20th century and the few to win a Nobel Prize (in literature), thought that understanding the natural numbers would provide a way to understand all of mathematics. His great work, the Principia Mathematica (written together with the mathematician and philosopher Alfred Whitehead), aimed to provide a foundation that would explain and justify all mathematical knowledge. The reading for today, an excerpt from his Introduction to Mathematical Philosophy, is an attempt to make the ideas of his more difficult work more accessible.

Bertrand Russell (1872-1970)
Russell began with the observation that, thanks to the work of several centuries of mathematicians, it appears that all of mathematics can be constructed from the natural numbers. This incredible idea, if correct, might make understanding how mathematics works a simpler task: if we could understand the natural numbers, then everything else would follow automatically.
For example, you can use natural numbers to construct the negative numbers using subtraction: define \(-2\) to be the number that you get when you subtract 2 from 0. More generally, let \(-n := 0 - n\). The set of natural numbers together with the negative numbers are called integers.
Similarly, notice that fractions can be constructed as pairs of natural numbers, one in the numerator and one in the denominator. These fractions are sometimes called rational numbers.
\(\tfrac{1}{2}, \tfrac{5}{3}, \tfrac{7}{8}, \tfrac{3}{4}, \dots\)
Are all numbers rational? It turns out that the answer is no: there are certain numbers that cannot be written as a fraction. This fact was discovered by the ancient Greeks. Here is one way to see how they thought about this in that time.
Suppose a painter is painting tiles, which come as both large and small squares. It happens that a small tile with a side-length of 1cm requires exactly 1g of paint to cover. And, a large tile with a side-length of 2cm takes 4g to cover.
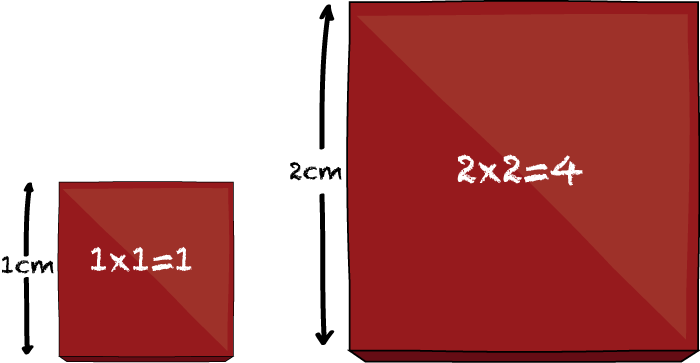
One day, the painter finds a medium-sized tile, and notices that it takes exactly 2g of point to cover. Since she's always been fascinated by mathematical questions, the painter asks: what is the side-length of this new tile? Whatever it is, we'll call that number \(\sqrt{2}\). It is a number that, when multiplied by itself, is equal to the number 2. The question is then: is it possible to writ the number \(\sqrt{2}\) down as a rational number?, i.e. in terms of pairs of rationals? More precisely, can we can find two natural numbers \(a\) and \(b\) such that \(\sqrt{2} = \frac{a}{b}?\)
If a number is not rational, then it is called irrational. So, another way to put our question is this: Is \(\sqrt{2}\) rational or irrational?
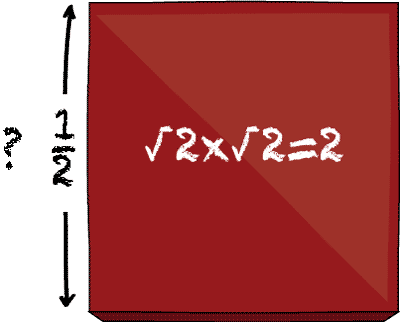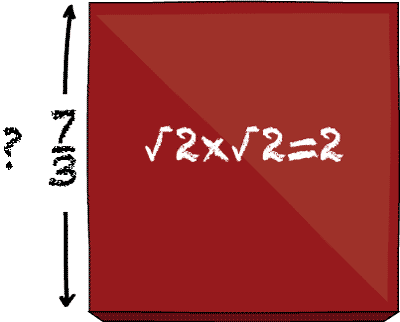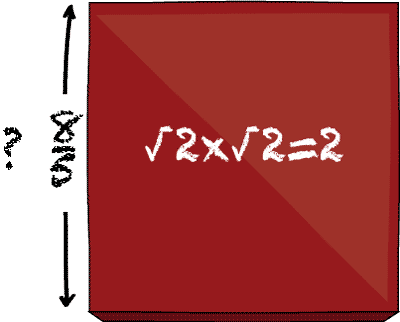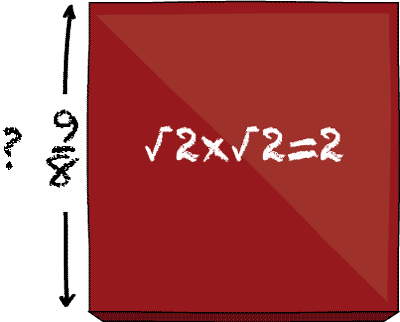
The answer, it turns out, is: irrational — there is no way to write \(\sqrt{2}\) as a fraction. The proof of this is elegant and a good example of mathematical proof in action; you can see it by clicking below.
Proof that \(\sqrt{2}\) is irrational
The problem of how to express \(\sqrt{2}\) using natural numbers didn't come until hundreds of year later, in the 19th century, when Cauchy discovered that irrational numbers can always be written as a special sequence of decimals. That is, there is a particular sequence of decimal numbers that, if carried on forever, would describe exactly the value of \(\sqrt{2}\):
1.41421356237....
In fact, such a sequence exists for every rational and irrational number. And, since a decimal sequence is composed out of natural numbers, it can always be constructed from the natural numbers in the same way. So, the natural numbers are again enough! The collection of rational and irrational numbers, each expressible in terms of its decimal expansion, is called the set of real numbers.
Can other areas of mathematics be constructed from the natural numbers in a similar way? It sure seems so. For example, think of geometry. One way to view Descartes' discovery of this description is the discovery that the Euclidean plane can be constructed from pairs of real numbers. And real numbers, we have just learned, can be constructed from the naturals!
A Cartesian plane: constructed from pairs of real numbers, which are constructed from natural numbers.
Indeed, it seems that everything in mathematics can be built out of the natural numbers. This leads to a tantalising possibility: if we can understand where the theory of natural numbers comes from and how it is justified, then we can use it to construct all of mathematics. So, we have reduced our problem to a simpler one: what is a natural number?
This question turns out to be harder than it first appears.
What is a natural number?
Let's begin with a few preliminary remarks about Russell's perspective on numbers, before building up the full picture.
Numbers as abstractions
One of Russell's central arguments is that numbers are abstract, rather than concrete.
For example, we can talk about a dozen eggs, or a dozen donuts. But neither one is enough to describe the number 12 itself. Rather, each is an instantiation of the number 12. An instantiation is a concrete example of a particular number. But the number itself is more abstract.


A dozen eggs and a dozen donuts are just examples of the number 12. According to Russell, neither one 'is' the number 12.
Russell refers to an instantiation of a number like '12 donuts' as a plurality. So, in Russell's language, the pluralities above are instantiations of the number 12, and the number 12 is an instantiation of a number. So, the concept of a number is quite abstract indeed!
Russell's perspective, that numbers are abstract, suggests that an adequate account of what a number is ought to explain why mathematics is not concrete. The logician Gotlob Frege put the problem in these colourful terms: suppose someone were to identify Julius Caesar with the number 2. That would be a bit inconvenient. But more importantly, according to Frege, it would incorrectly identify what the number 2 is. Julius Caesar was a man, a Roman, and a conqueror — but he was not a number. Frege's use of this example is so famous that it has a name in philosophy, the 'Julius Caesar Problem'.
The Julius Caesar Problem: An adequate account of numbers must be capable of explaining why Julius Caesar is not a number.
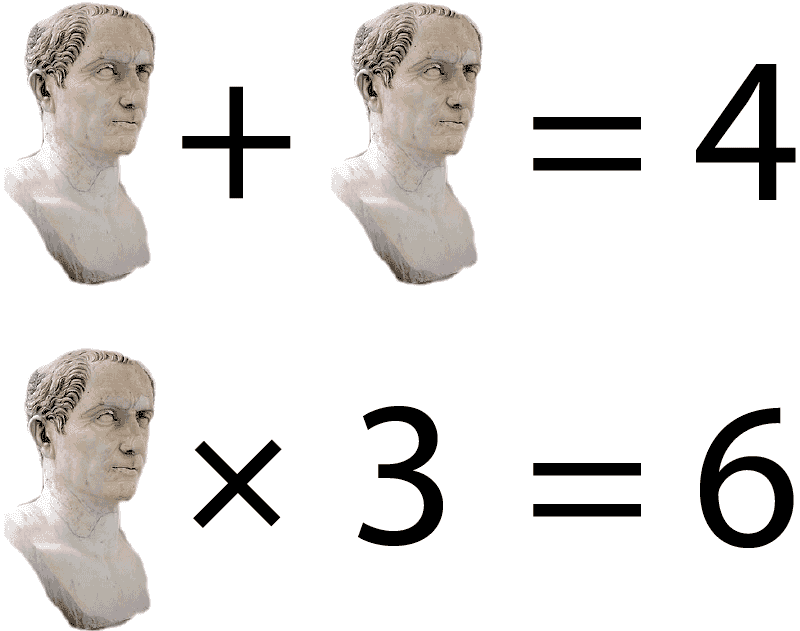
The Julius Caesar Problem: To explain why it is wrong to treating Caesar like, say, the number 2.
The claim that numbers are abstract also appears to constrain the nature of truths about numbers. Following Kant, many philosophers (including Russell) distinguish two different kinds of propositions, on the basis of what determines their truth.
An analytic proposition is one whose truth is determined by the meaning and arrangement of the component terms.
A synthetic proposition is one whose truth is determined by the states of affairs that the proposition represents.
A famous example of an analytic proposition is the statement: All bachelors are unmarried. Once you understand the meanings of the words in the proposition, you know that it must be true: this is what it means to be analytic. In contrast, a statement like, The solar system has nine planets is synthetic, since its truth can only be determined by examination the facts about the solar system being described.

'All bachelors are unmarried':
An analytic proposition
'The solar system has nine planets':
A synthetic proposition
Typical examples of analytic truths are logical truths, sometimes called 'tautologies'. But Russell believes that mathematics is analytic as well. That is, the truth of a mathematical proposition is determined entirely by the meaning of the component terms, and not by its relation to any concrete thing in the world. So, however we proceed, our account of numbers should help us both understand why a number is abstract, but also why the propositions of number theory are analytic.
Peano's remarkable axioms
How can we come to understand what a number is? One clever way to approach this question would be to think of it as analogous to asking what geometry is. Euclid answered this question by postulating a small number of axioms or assumptions about points and lines, and showing that all of geometry could be deduced from those axioms. It would then be possible to define (Euclidean) geometry to be anything that satisfies Euclid's axioms.

Pages from Byrne's edition of Euclid's Elements
Can we do the same thing with numbers? That is, can we view numbers as just something that satisfies some particular axioms? One promising first approach to understanding what numbers are was formulated by the Italian linguist and mathematician Giuseppe Peano in 1889. He wrote down a list of axioms now known as the Peano axioms of arithmetic. Peano proposed three basic concepts, analogous to the points and lines of Euclid:
number, successor, 0
The term 'number' can be thought of here as just a label for the concepts that we wish to define. Intuitively, 'successor' refers to the 'next' number in a list. The last concept is read, 'zero', and will play the role of what you intuitively understand by zero. Peano tried to give these basic concepts meaning by proposing that these five axioms.
The Peano Axioms
- 0 is a number.
- The successor of any number is a number.
- No two numbers have the same succcessor.
- 0 is not the successor of any number.
- Any property which belongs to 0, and also to the successor of any number that also has that property, belongs to all numbers.
Incredibly, these concepts and axioms appear to express everything about numbers. The information about all of arithmetic, vast though it may seem, is actually compressible into the tiny box above! For example, suppose we wish to define the number 1. We have 0, and the axioms say it has a successor. So, we can define 1 to be the successor of zero. Similarly,
- Let '2' refer to the successor of 1
- Let '3' refer to the successor of 2
- Let '4' refer to the successor of 3
:
What else do we want to know about numbers? Suppose I want to define addition. That is, given any two numbers \(n\) and \(m\), we want to know how to define \(n + m\). We can do this in two steps:
- Define \(m+0\) to be \(m\)
- Define \(m + (n+1)\) to be the successor of \(m+n\)
The second point implies for example that \(m + 1\) is the successor of \(m\), and \(m + 2\) is the successor of \(m+1\), etc. So, this definition of addition seems to match how we intuitively understand the concept. This seems very promising! Perhaps we can just define numbers to be anything that satisfies the Peano axioms.
One problem with this approach is that it doesn't solve the Julius Caesar problem. Indeed, if the Roman conqueror Julius Caesar happened to be included in a collection that satisfies the Peano axioms, then he would indeed seem to be a 'number' on this definition.
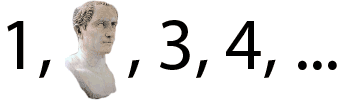
The Caesar problem strikes: Nothing seems to prevent 'numbers' that include Caesar from satisfying the Peano axioms
Russell points out that there is another major problem with this approach: there appear to be multiple, distinct kinds of structures that satisfy the Peano axioms. For example, suppose by 'number' we mean what is normally called an 'even number':
0, 2, 4, 6, ...
And suppose that we use 'successor' to refer to what is normally meant by 'adding two'. Then we get another structure that satisfies the Peano axioms. And in fact there is an infinitude of different structures that all satisfy the Peano axioms. So, which one is correct?
The answer cannot be given using only the Peano axioms. We must come prepared with an independent understanding of the basic concepts of number, successor and 0. Otherwise, we don't really know what 'a structure satisfying the Peano axioms' refers to. But this seems to put us right back to where we started. What is a number? What is a successor? What is 0? It seems we will need a different approach.
Logicism
Frege's Strategy
The solution that Russell adopts follows a strategy due to Gottlob Frege. A German logician, mathematician, and philosopher, Frege had an enormous impact on modern philosophy of language, logic and mathematics (in part through his influence on Russell).

Gottlob Frege (1848-1925)
Frege's strategy was set out in a two-volume work called the Foundations of Arithmetic (often referred to as the original German Grundgesetze der Arithmetik), with the volumes published in 1893 and 1903, respectively. These works were intensely studied by philosophers and mathematicians, and contain many deep and fascinating twists and turns. But the basic, guiding principle of the work is simple: that all of mathematics is nothing but logic. This makes intuitive sense in many ways. Mathematics certainly involves a great deal of logical reasoning. But it is a more radical philosophical view to say that mathematics is nothing more than a part of logic. This view, known as Logicism, was adopted by Russell as well.
Logicism: The claim that mathematics is reducible to logic. Logicists assert that mathematical truths are just logical truths; or, that mathematical proofs are just logical proofs; or both.
The statement of logicism is interesting because it is both a philosophical perspective as well as a mathematical conjecture. We must certainly ask, as philosophers, what exactly it means to 'reduce' or 'define' mathematics to logic, and whether this is an appropriate way to understand mathematics. But we must also ask, from a purely mathematical perspective, whether such a definition is even possible!
To clear the way for the mathematical conjecture, Frege and Russell begin with some philosophy.
Extensional and Intensional Definitions
What does it mean to say that mathematics 'reduces' to logic? Frege and Russell give this an obvious interpretation: that mathematics can be defined using only the language of logic. To begin to understand this, it is helpful to distinguish two kinds of definition.
Extensional definition: A definition by enumeration of examples.
Intensional definition: A definition by identification of a defining property.
For example, suppose I wish to define the authors of Principia Mathematica. An extensional definition would enumerate all the examples: Authors = {Russell, Whitehead}. An intensional definition would give a defining property: Authors = 'People who contributed to the writing of Principia Mathematica'.

Principia Mathematica: Russell and Whitehead's Logicist foundations for mathematics
Because an extensional definition requires formulating a list of examples, these kinds of definitions are often intractable. For example, suppose I wish to define 'the human inhabitants of London'. How would I give an extensional definition of this? I would have to make a list that includes every single human in London. If such a definition is possible at all, then it is enormously impractical.

Inhabitants of London: an extensional definition is impractical, if not impossible.
A much more practical way to define 'the human inhabitants of London' would be to give an intensional definition of Londoners, for example that they are humans whose permanent residence lies within the M25 boundary highway.
With numbers, the possibility of an extensional definition is even worse: there are infinitely many natural numbers. So, an extensional definition of numbers is not just impractical: it is totally impossible for a human with a finite lifetime. Indeed, giving an extensional definition of even one number like '3' seems to be impossible, since there may well be an infinitude of concrete 'trios' that we would have to list!
If we are going to have any success at all in defining numbers in terms of logic, then we must define numbers intensionally. The aim is then to characterise the 'defining properties' of numbers, using only the language of logic. This is what Russell, as a logicist, takes his philosophical and mathematical challenge to be.
Hume's Principle
The definition of a number that Russell adopts, which again arises in the work of Frege, makes use of the powerful concept of a one-one relation, sometimes called a 'bijection' or a 'bijective relation'.
A one-one relation is a function from one set or class A to another set or class B, with the properties that (i) that element of A is mapped to exactly one element of B, and (ii) for each element x in B, there is an element y of A that is mapped to x.
Here are some examples:
The relation of mother and eldest child is a one-one relation. Every mother has exactly one eldest child; and, every eldest child has a mother.

Picasso, 'Mother and Child'
The relation between sides and corners of a quadrilateral is one-one: every corner can be associated with one side, and every side can be associated with one corner.

Quadrilaterals: the sides and corners stand in a one-one relation.
You can see the general way that a bijection looks by drawing a picture of the two sets or classes. A one-one relation is then one that pairs all the elements of the sets.
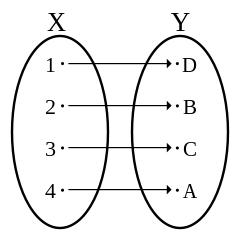
A bijection between two sets X and Y
In contrast, the following two relations are not one-one:

Not a one-one, because not every element of Y is paired with an element of X.
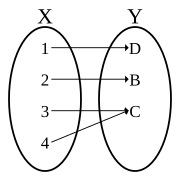
Not one-one, because a pair of elements in X are mapped to the same element in Y.
As you should be able to see from the examples above, a sets of the same number stand in a one-one relation. Indeed, if there is a one-one relation between two sets, then we call the two sets 'similar', or 'equinumerous'.
Frege's brilliant idea was that one can turn this observation around, and use it to define numbers intensionally in terms of one-one relations between sets. The definition proceeds in two steps. The first is an idea that traces back to David Hume, and is named after him.
Hume's Principle. Define the 'number of a class/set' to be the collection of all those sets that stand in a one-one relation with that class/set.
As our intensional definition of Londoners, this intensional definition of a number does not enumerate the examples, but rather identifies a defining property: standing in a one-one relation. On this definition, the 'number of donuts' in a box is the set of all the things that stand in a one-one relation to the box. This includes other boxes of donuts, cartons of eggs, and many other things, all of which share this defining property.
With Hume's principle in hand, we can now finally give the Logicist definition of a number:
Logicist definition of a number. Define a 'number' to be "anything which is the number of some class" or set.
This seems to be a very powerful definition indeed. It is certainly abstract: a number is not any particular concrete, but rather a giant collection of possibly-concrete things. It is also clear that Julius Caesar is not a number on this definition: he is a man, a Roman, and a conqueror, but he is not a collection of all sets related to a given set by a one-one relation.
Most importantly, this definition makes use of only terms that can be plausibly identified as 'pure logic'. Sets and one-one relations are central objects in a certain mathematical approach to logic known as set theory. So, by defining numbers in terms of one-one relations and sets, we have something that can plausibly be called a 'reduction of numbers to logic'. Insofar as all of mathematics can be reduced to numbers, this would imply that mathematics is indeed 'just logic' as the Logicist set out to show.
This gives us a powerful explanation of both the justification and the truth of mathematics. Mathematics is justified because it is deducible from pure logic. And the results of mathematics are true because the tautologies of logic are analytic truths, determined only by the meanings of the terms.
Problems for Logicists
Logicism is an impressive and ambitious project to explain why mathematics works. However, its success depends on the extent to which various problems with this view of mathematics can be overcome. Here are a few of them; more can be found here.
- The analyticity problem. How can one demonstrate that the logical propositions are analytic? Without this, the security of the truths of mathematics remains unexplained.
- The conceptualisation problem. How is it that we come to know number? People have known facts about number for thousands of years without going through the detailed reduction procedure that the logicist describes. How is this possible? And given that it's possible, is logicism really necessary?
- The problem of multiple logics. There appear to be many different systems of logic that disagree. Which one is the correct foundation for mathematics?
- The problem of mathematization. It is not clear that all of mathematics can be reduced to logic. What argument can be given for this?
Two alternative philosophies of mathematics
Platonism
One alternative to logicism is a view called platonism. It is a realist perspective on the numbers, and on mathematical objects more generally. The platonist view is that, just as empirical reality is the source of a posteriori truth, so mathematical reality is the source of mathematical truth. That is, that written into the universe there is a mind-independent fact about numbers, and perhaps even that certain numbers 'exist' (though not in space and time). Somehow, humans come to detect this mathematical reality with their minds, and when we prove theorems in mathematics we are discovering the nature of that mathematical reality.

The platonist response does very well at explaining what the source of mathematical knowledge is, and especially why it is so compelling: mathematics just describes the way we detect mathematical reality to be. But it has at least two difficulties.
The first is how we could possibly have access to such a non-empirical aspect of reality. Our sensory access to the world, and even the way our brains process those sensory perceptions, seem rooted in empirical processes. How is it that we come to detect facts about a supposedly non-empirical aspect of the world?
The second difficulty is that, given the separation between mathematical and empirical reality, it is enormously puzzling why mathematics is so effective in describing empirical phenomena. We noted above that mathematics has applications in almost every area of human thought. Often these applications are unexpected. This led the physicist Steven Weinberg to say,
"It is positively spooky how the physicist finds the mathematician has been there before him or her."
Thus, although the mathematical platonist has a good explanation of the source of mathematical truths, as well as why those truths are so compelling, the story is less convincing when it comes to our access to those truths and our ability to apply them.
The mathematical antirealist response
If these difficulties are insurmountable, then one may be led to adopt the mathematical antirealist response to the problem. This view asserts that there is no special, mind-independent aspect of reality corresponding to the mathematical realm. The source of mathematical truths is the same as the source of any other truths.
A common form of mathematical antirealism, advocated by the great 20th century mathematician David Hilbert, is the conventionalist view of mathematics. This begins with the perspective that mathematics is just about symbols and symbol-manipulation.

A Mayan manuscript containing the Mayan system of numerals and symbol-manipulation.
The conventionalist approach to mathematical antirealism treats mathematics like the game of chess. The rules of chess are conventional. They are an entirely human invention, which could have been very different. Nevertheless, the rules of chess are very strict, allowing only certain kinds of play. It also guarantees certain facts to a high degree of certainty, such as the fact that certain attacks or defences are possible.

To the conventionalist, the rules of mathematics are just ordinary human-agreed rules, like the rules of chess
The conventionalist approach to mathematical antirealism accommodates the empiricism. In particular, the conventionalist is able to view mathematical truths like 2+3=5 as a posteriori. However, this does not imply that the ultimate justification of mathematics is through inductive inference on observational evidence. We don't justify 2+3=5 by observing many successive combinations of 2 and 3 objects.

Even for the conventionalist, the justification of 2+3=5 is that it follows from a rule of arithmetic. But the justification of that rule, according to the conventionalist, is that humans have pervasively agreed to adopt it as a matter of convention. No further justification is needed.
This general tension between platonism and antirealism in mathematics can thus be summarised: the more metaphysical significance we give to mathematical truth, the less epistemological access we allow; and the more epistemological access we allow, the less the metaphysical significance. This is known as Benacerraf's problem, after the Princeton philosopher Paul Benacerraf who first proposed it. (Original article here.)