Short Answer Questions (submit online)

1. What is wrong with what Goodman calls the 'Most Naïve' or 'Resemblance' account of representation?
2. Explain the Peirce/van Fraassen 'Of-As' view of representation.
3. Why does Wigner say that the effectiveness of mathematics in science is 'unreasonable'?

For Further Discussion

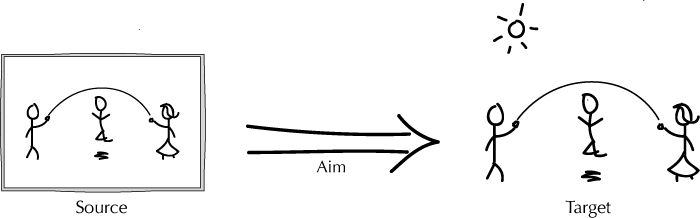
• The structure of a representation. We have characterised representation as a certain kind of relationship between a source and its target.
  • According to Peirce, representations fall into three categories: 1) iconic representations, which resemble their targets, 2) indexical representations, which display causal relations, and 3) symbolic representations, which denote their target. Try to give an example of each.
  • Is everything a representation of itself? Is anything a representation of itself?
  • If X is a representation of Y, does it follow that Y is a representation of X? Is it ever possible to have a situation in which X and Y represent each other?
  • If X is a representation of Y, and Y is a representation of Z, does it follow that X is a representation of Z? Under what circumstances (if any) might this follow?
• The Most Naïve 'Resemblance' View. The simplest initial view of representation is that it is a matter of resemblance.
  • Give an example of a representation that does not resemble its taret.
  • Give an example of two things that equally resemble their target, but are not equally good representations.
  • Are there any special circumstances under which the resemblance view of representation is correct? What might those circumstances be?
• The Of-As View of Representation. The Of-As view of representation involves three components: a target, a source, and a use/aim.
  • How are those targets supposed to be related?
  • Give an example in which two source representations have the same target, but are different, because of a differing use/aim.
  • Give an example in which the same source representation can have two different targets, because of a differing use/aim.
  • We described the representation relation as involving an arrow. What does that arrow represent?
• The unreasonable effectiveness of mathematics. Mathematics provides a number of different kinds of representations that are incredibly effective at describing the world, from equations to graphs to abstract diagrams.
  • Do you find this unreasonable?
  • Why would it be reasonable if we thought that mathematics shares an aim with science?
  • Wigner thought that the aims of mathematics and science were very different. Why? Do you agree with him?
  • Is mathematics really all that effective? If so, what do you think explains the effectiveness of mathematics in science?