Revision or Bust
It can be hard to trust something when we don't know how it works.
For example, you might have heard of the late Paul the Octopus, an English octopus from Weymouth who became famous for his 2010 World Cup predictions in Oberhausen, Germany. For each of the World Cup matches involving Germany, Paul would be given two boxes of food. The boxes were identical except for the flags of the teams displayed prominently on the front. Each time, Paul would choose to eat from one box of food first. Each time Paul chose the box displaying the flag of the team that would win the day's match.

If Paul's choices were random, then his predictions were equivalent to correctly predicting the outcome 7 coin tosses in a row, for which you have a roughly 0.8% chance. Actually Paul may have had a slight preference for the German box, which makes the prediction somewhat more likely. Still, it is a remarkably unlikely sequence of events. But would you have trusted Paul with matters that are really important? With your choice of university? With your choice of lover? With your choice of job?
I'm guessing that you would not. Paul is just an octopus. He did have a remarkably lucky run on a few isolated occasions, but there is no reason to trust his continued success. And if we look carefully, we could likely produce plenty of reasons not to trust his continued predictions.

This was Karl Popper's reaction to inductive confirmation as well. Of course inductive confirmation in science is an incredibly successful practice. But as we saw last time, the initial naïve attempts to justify it fail. We need to either produce a more sophisticated account or give up on induction.
Karl Popper chose the latter. Let's briefly consider that option before returning to the former.
Popper's anti-inductivism
You have probably heard of Popper's most famous catch-phrase, real science must be falsifiable. His advocacy of this view had an long-standing influence on scientists in both the natural and social sciences, in part because of Popper's extensive engagement with both at LSE.

However, this is not what Popper was saying, nor is it even his idea.
As you know from Lecture 2, the logical empiricists were demanding that meaningful statements be subjectable to empirical tests, which could involve either verification or falsification. The main thesis that Popper advocated was to deny that verification is possible according to schemas like inductive confirmation. In other words, Popper denied the possibility of inductive confirmation.
Popper was in part concerned with the lack of a reason to believe that induction works, much like the predictive powers of Paul the Octopus. But he was also concerned that inductive confirmation was responsible for some of the greatest failures of science.
For example, the physicists George Ellis and Joe Silk recently published an article in Nature arguing that, due to the systematic tendency of many recent theories of physics to be adjusted or "tuned" so as to match almost any data whatsoever.

For example, supersymmetry is a recent theory that has consequences for what kinds of particles there are. But, according to Ellis and Silk, proponents of supersymmetry can always adjust the taxonomy of particles to match observations, no matter what we happen to observe.
Similarly, the multiverse is a proposal that our universe is just one of universe out of many that is constantly emerging from a giant manifold of universes. But, they say, multiverse proponents can always adjust the facts about these mini-universes (such as their curvature) to match observations where necessary.

The problem is that a theory that can account for anything accounts for nothing at all. It can describe falsehoods as well as it can describe truth. There is no reason to trust it.
According to Popper, the source of the problem is inductive confirmation. To avoid it, he argued, one must believe only what has been falsified and not what has been "confirmed". That is, one must deny the possibility of inductive confirmation. To do otherwise leads one to the belief in illegitimate multiverses, supersymmetries, and octopus oracles.
Of course, Popper did think that some theories were more worthy of our consideration than others. The theories that had this character were said to be corroborated. However, one must not mistake corroboration for confirmation. Induction gives us no reason to adjust one's belief in the truth of a theory. At best, it suggests theories that are worthy of our consideration.
Popper's view is extremely radical, much more so than the simple slogan that science out to be falsifiable. It denies much of what many scientists believe, that we have reason to believe in the truth of some of our best theories of science. It is indeed so extreme that the majority of philosophers of science reject it as implausible.

The Pittsburgh philosopher Wesley Salmon summarised its most serious difficulty: we use induction to guide our predictions in science, a practice that seems to make absolutely no sense on Popper's view. A theory having been "corroborated" and thus made worthy of our consideration provides no reason whatsoever to believe that it will make the correct predictions. On the other hand, if a theory receives inductive confirmation, then we have more reason to believe that it is true than we did before, and so we are justified in using it to make predictions.
Perhaps all that is needed, then, is a more sophisticated account of inductive confirmation. Let us turn to the possibility of such an account now.
The Bayesian approach

An alternative to Popper's radical denial is to add structure to our account of induction to make it considerably more powerful. A simple and obvious idea, so helpful that you may have thought about it already, is to make confirmation a matter of degree.
In short, instead of asking whether evidence confirms a hypothesis, we will ask how much we should believe in the hypothesis, on a scale from 0 (not at all) to 1 (certain). When we receive evidence that confirms a hypothesis, this means that we now have more reason to believe the hypothesis.
It's just like the way that accumulating evidence of a courtroom can gradually increase the jury's belief that the defendant is guilty.

How much is our belief in a hypothesis raised or lowered when we receive a piece of evidence? It depends on what kind of evidence it is. One normally describes the situation as follows.
Say you're interested in a hypothesis H, such as "It will rain in London today", and that we're considering the evidence E that "There are no clouds in the sky this morning". How much should the evidence of the clouds adjust your belief that it will rain? Let's take a concrete situation.
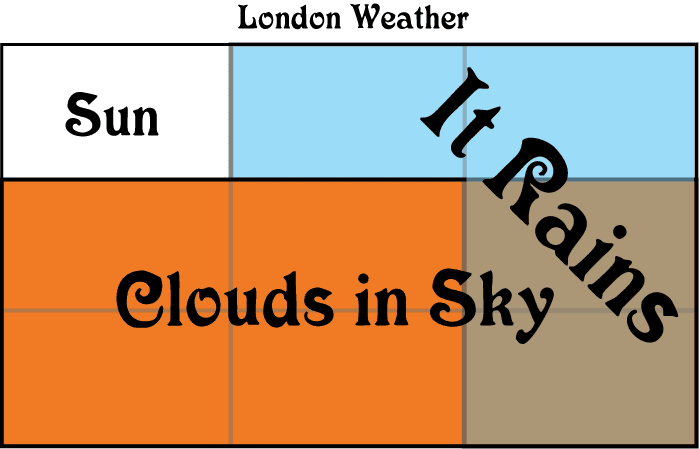
The blue and brown squares in the diagramme indicate the portion of days that it rains in London, roughly 4 out of every 9. So, without any further evidence, there is a 4/9 = 0.44 chance of rain.
How does the evidence of seeing clouds change this probability? The diagramme is telling me that it usually rains even when it is not cloudy. In particular, I know that there are no clouds in the morning on 3 out of every 9 days, as indicated in the orange/brown squares in the grid. But it rains on 2 out of 3 of those days without clouds in the morning. So, given that I've seen clouds, there is a 2/3=0.66 chance of rain.
In other words, if this diagramme is accurate, then seeing no clouds in the morning provides confirmation for the theory that it will rain. In particular, it raises my belief in rain from 0.44 to 0.66.

This situation is described precisely using conditional probability. Confirmation occurs when a piece of evidence E increases our belief in a hypothesis H if the probability of "H given E", written P(H|E), is greater than the probability of H alone, written P(H). In the case above, we found that P(H)=0.44 and P(H|E)=0.66, so this is an instance of confirmation.
On the other hand, disconfirmation occurs when a piece of evidence E decreases our belief in a hypothesis H, in that P(H|E) is less than P(H).
The view that probability theory can be used to describe the confirmation and disconfirmation of a hypothesis in science is known as the Bayesian approach to confirmation. It is at the same time an extremely general approach to confirmation, as well as an extremely popular approach among philosophers of science. It may be summarised as the following two principles:
- Inductive confirmation is a matter of degree (between 0 and 1).
- The conditional probability Pr(H|E) determines how we should update our degree of belief in the confirmation of a hypothesis H, whenever some evidence E is introduced.
One advantage of this revision of inductive confirmation is that it makes immediate sense of the Raven Paradox discussed last time.

In particular, we now have now problem saying that observing a white show confirms that all ravens are black. The degree of confirmation is just exceedingly small. Although we have narrowed the number of non-black things that are non-ravens, the enormous size of this class of things means that it does little to confirm that all ravens are black. Observing a large portion of the total number of ravens, on the other hand, provides a much larger degree of confirmation on the Bayesian approach.
Difficulties with Bayesian approach
There are a number of well-known difficulties with the Bayesian approach.
- How do we set the probabilities in the first place? We could only do our calculation with the rain because we know the portion of days that it rains, the portion of days that its cloudy, etc. How do we assign these probabilities? The Bayesian account provides no way to do this, and it is not obvious how any particular way to assign probabilities can be justified. This is called the problem of the priors — no "prior" probability of a hypothesis P(H) is not justified on the Bayesian account.
- No way to describe ignorance. On the Bayesian picture, P(H)=0 implies a hypothesis has been falsified with certainty, while P(H)=1 implies that it has been confirmed with certainty. P(H)=1/2 implies that there is an equal chance that the hypothesis be true or false. But nothing is said about the situation in which one is completely ignorant. For example, suppose you have a coin that you suspect is biased, but you have no knowledge whatsoever about that bias. What probability should you assign to the outcome that it lands heads? The Bayesian approach has no way to even describe this situation, let alone make a prediction.
- Probabilities cannot always be assigned. The current universe is thought to be spatially infinite. But all probabilities of events occurring in finite regions of an infinite universe are zero. So, no non-trivial probabilities can be assigned in this context. Nevertheless, scientists are able to do cosmology and collect evidence about the universe as a whole. The Bayesian approach has no way to describe this.
Norton's Material Theory
John Norton points out that there are three main approaches to induction so far on the table.
- Naive Induction, which has the problems discussed last time of lack of sophistication.
- The Hypothetico-Deductive Theory, which falls prey to problems like the Raven Paradox. (Norton views Popper's falsificationism as a radical special case of this theory.
- Bayesianism, which gets stuck on the problem of priors, among the other problems described above.
According to Norton, the problem with all these approaches is that no inductive inference schema can be expected to work in every case. He gives a very simple example to illustrate.
Consider any argument that bismuth melts at 271°C, and compare it to any inductive argument that wax melts at 90°C.

.jpg)
These sentences have exactly the same grammatical form. And any argument concerning them that uses the approaches to induction above will have the same logical form. So, these general approaches to induction should generally take these two statements to be equally confirmed.
But this is absurd — although it is a chemical fact that Bismuth always melts at a fixed temperature, there is no such guaranteed fax about wax; indeed, wax melts at many different temperatures, and which temperature it is depends on its precise composition.
Instead, Norton proposes what he calls the material theory of induction, by which the reason one can make this inference is by appeal not to any universal schema, but to particular chemical facts. In the case of Bismuth, it is the fact that it is a chemical element that it can be expected to have a fixed melting point. Hence Norton's slogans, material facts are what power induction.
Norton can give many similar examples in the history of Newtonian physics:
- The inductive inference to the existence of Neptune was powered by Newton's laws
- The discovery of the tides was powered by Newton's laws.
But one may still wonder, what justifies the material facts? In this case, Norton's answer is the same as before: further material facts.
Now you may be wondering if there is a danger of a regress. Norton admits that this regress exists, but does not think that it is too dangerous. He assumes instead that such a regress will eventually "bottom out" with facts that are justified by brute observation, with no further inductive steps needed. The success of his account therefore depends on whether or not this is possible. Is it?
This is a problem that I leave to you to decide.
What you should know
- Popper's anti-inductivism and its problems
- The Bayesian approach
- The Bayesian problem of the priors, problem of ignorance, and problem of not being able to assign probabilities.
- Norton's material theory, and Norton's solution to the regress problem.