Thinking like a physicist

In recent years many physicists have become researchers in economics. Hundreds of people are now working in this field, which was dubbed econophysics by physicists Rosario Mantegna and Eugene Stanley. Mantegna is currently a Professor of Economics. The field is thriving, with thousands of papers archived at the Econophysics Forum, hosted by the University of Fribourg.

Although the role of physics in economics has been experiencing unprecedented growth, this is not a new phenomenon. Many of the great minds of 20th century finance had extensive training in physics and applied mathematics. Louis Bachelier, one of the founders of quantitative finance, was trained by Henri Poincaré, a mathematician, physicist and philosopher. Fischer Black, famous in economics for having co-discovered the Black-Scholes equation, studied applied mathematics and physics at Harvard. And James Simons, arguably the world's most successful hedge-fund manager, began his career as a PhD in mathematical physics.

It turns out that in modern economics, it is helpful to think like a physicist. Physicists tend to pursue ideas from a unique perspective, which involves,

1. Developing precise conceptual ideas and tools; and
2. Seeking broad abstract connections between different materials, scales and physical systems.

Instead of emphasising the differences between physical systems, thinking like a physicist often means finding the similarities. For example, Galileo showed that bodies experience free-fall due to gravity in the same way, no matter what shape, mass, colour, smell, or any other property they happen to have.

Conceptual tools that make abstract connections turn out to be particularly useful in finance. And one particularly brilliant conceptual tool, which connects many very different phenomena of conceptual and had an enormous impact on both physics and finance, is the notion of a random walk. To introduce it, let's begin with an example.

Einstein's brilliant thought about water

Einstein developed a powerful new way of thinking in order to understand the behaviour of a relatively large molecule suspended in water.

The theory of 19th century thermodynamics explains the basic ways that macroscopic bodies transfer heat, energy and work. For example, it explains how heat can be converted into work in an engine. It also explains how a cube of sugar placed in your tea will dissolve and spread throughout the liquid. However, it said almost nothing about the nature of the liquid or sugar itself on a microscopic level.

What would we see if we were to zoom in on an individual molecule of sugar in that cup of tea? Classical thermodynamics says nothing at all about this question. The microscopic scale is completely irrelevant for understanding classical thermodynamics. That's part of the beauty of that theory: substances obey the laws of thermodynamics regardless of what they are made of. And those laws just say the sugar will spread throughout the cup.

However, if you could zoom in enough to see the molecular composition of your cup of tea, you would in fact see an roiling swarm of atoms careening about, in every which direction, and in unimaginably large numbers.

These atoms of water will inevitably collide with the sugar molecule. How often does this happen? Suppose we restrict attention to a very small interval of time, say a hundredth of a second. In this little interval of time, atoms of water will collide with the sugar molecule roughly 10 trillion times. The average effect of all those collisions is to make the sugar molecule move a little bit in some direction. In the next hundredth of a second interval it will move again. In the next interval, again. The result is a subtle "jiggling" of the sugar molecule about.

This jiggling phenomenon is known as Brownian motion, named after the Scottish botanist Robert Brown who observed it in 1827. (You can freely read Brown's report on Google books). Sugar molecules are actually too small to observe their Brownian motion through an ordinary microscope. However, you can see it when you look at milk diluted in water; in the video below, fat globules from milk experience a jiggling motion due to their collision with water molecules that are too tiny to be visible. The field of view in the video is about 7 hundredths of a millimetre wide.

When a molecule experiences Brownian motion, we can't possibly predict its trajectory. To do that would require us to keep track of 1,000 trillion collisions a second, even if they were visible. That is, we are in a state of ignorance about the molecule's motion. However, because the tiny particles are roughly uniform in the way they careen about, we can still assign probabilities to the possible outcomes. For example, a molecule in Brownian motion is just as likely to move up as it is to move down.

Moreover, since we are really totally ignorant of exactly how the particles are colliding, the motion of the Brownian molecule tells us nothing at all about what it will do next. Suppose we observe molecule again during a one-hundredth of a second interval, and find that it moves up. This tells us nothing about it is going to in the next interval. That is, the particle's motion at each interval of time is probabilistically independent from every other interval.

This motion is an example of what is called a random walk. Brown himself only observed this phenomenon, and didn't know what to make of it. But Einstein used this kind of thinking in no less than three of his most famous papers, which we will discuss in the next chapter. To define it precisely, we will need to review some of the key concepts that make it work.

Probabilistic Thinking

Random walks are a tool of probability theory, a theory that allows us to make predictions about certain kinds of uncertain outcomes. What is probability theory about?

The real scoundrel's mathematics has always been the study of probability. Probability was largely developed to win at games of chance and bet on people dying. Although this kind of gambling had been played for thousands of years, it became institutionalised in Europe with the advent of casinos, and with the industry of maritime life insurance, both of which arose in the 16th and 17th centuries.

Probability theory is a lot like Euclidean geometry, in that it is a defined as an axiomatic mathematical framework, which turns out to be incredibly accurate at describing various aspects of the physical world. In fact, all of probability theory comes out of just three axioms, first stated in this way by the Russian mathematician Andrey Kolmogorov in 1933. They are about a function \(\Pr(x)\) called a probability distribution, which you should read as, "The probability of \(x\)".

More details about the probability axioms

×Close

The Probability Axioms

Axiom 1. Probabilities are numbers between 0 and 1. A probability distribution is firstly an assignment of a number (the "probability") to each event^(*) that we wish to consider.

\[ \Pr(x) = n. \]

For example, the probability of flipping a fair coin heads is given by \(\Pr(heads)=1/2\). The probability of rolling a pair of fair dice is whose sum is 2 (i.e. "snake eyes") is 1/36.

(*) What is the precise definition of an event? Examples of events include the event that a coin lands heads, and the event that a coin lands tails. Mathematically, at least in classical probability theory, an event is taken to be a member of a particular kind of structure called a σ (sigma) algebra over a set. You can think of this as providing events with the structure of propositions. For example, events say something about the way the world is that can be true or false. And, if I can talk about an event, then I can talk about its negation, its conjunction and disjunction with other events.

People sometimes speak about probabilities as lying on a 0 to 100 scale. We will from now on adopt the convention on which probabilities take values between 0 and 1 (inclusive). So, if we're interested in those events that are the outcomes of the roll of a pair of dice, then probability assigns a number to each of those outcomes. For fair dice, each of the 36 outcomes is assigned an equal probability of 1/36.

Axiom 2. Something must happen. Even in situations of uncertainty, at least one of the possible outcomes must happen. For example, a regular die will always roll 1, 2, 3, 4, 5, or 6. This second axiom is often expressed as the condition that if \(S\) is the set of all possible outcomes, then,

\[ \Pr(S)=1.\]

Axiom 3. Exclusive disjunctions add. If two events cannot both happen at once, like rolling a 1 and rolling a 2 on a regular die, then the probability of their disjunction (i.e. of event 1 or event 2) is just the sum of their individual probabilities. That is, for mutually exclusive events we have,

\[ \Pr(x \text{ or } y) = \Pr(x) + \Pr(y). \]

And we assume the same holds for any number of repeated disjunctions. So, for example, we can ask what's the probability of rolling either 1 or 6 on a fair die? These two outcomes are mutually exclusive, so it's given by,

\[ \Pr(1 \text{ or } 6) = \Pr(1) + \Pr(6) = \frac{1}{6}+\frac{1}{6}=\frac{2}{6} = \frac{1}{3}. \]

More Practice: Simple Probability  

More Practice: Sample spaces  

Close

That's it! The entire theory of probability follows from just those three assumptions. Of course, it takes a little manipulation to get all the interesting stuff that follows from this. But we'll develop that when we need it (and if you can't wait, you can read my overview of probability and its philosophy here.)

There is just one derivative concept in probability that we will need right away, called a conditional probability. It is defined as follows.

Conditional Probability. The quantity \(\Pr(x \,|\, y)\), read "The probability of \(x\) given \(y\)", is defined to be,

This is just a definition, but it turns out to provide a very good definition of the intuitive meaning of conditional probability. For example, suppose we start our day knowing that the probability of rain is 0.5, or 50%. But by noon, we see that there are dark storm clouds. What is probability of rain given that there are storm clouds? The answer is given by the conditional probability, \(\Pr(rain\,|\,clouds)\). We would generally expect this particular conditional probability to be greater than \(\Pr(rain)\).

Conditional probability is important for us because it allows us to say exactly what it means for two events to be independent of one another. For two events \(x\) and \(y\) to be probabilistically independent means that the probability of \(x\) doesn't change when we learn that \(y\) has happened: the probability of \(x\) given \(y\) is the same as the probability of \(x\). Formally:

Probabilistic Independence: \(\Pr(x\,|\,y) = \Pr(x)\), i.e., the probability of \(x\) doesn't change if \(y\) occurs.

For example, if you flip a fair coin 100 times, the probability that each flip will land heads is 0.5. The probability of a given coin flip is completely independent of the flips that came before it. So, in particular, it doesn't matter if the coin happened to flip heads the first 99 times. The probability that the 100th flip will be heads is still 50-50!

More Practice: Probabilistic Independence  

Random walks

The random walk is sometimes called the drunkard's walk. The reason should be obvious.

A drunkard stumbles around a convenience store in an apparently random fashion. Each step is followed by a moment of becoming steady, and the direction of the step that follows is anybody's guess. It is equally probable that the drunkard's step will be in any given direction. And knowing the previous step tells you nothing about the next step. Each step is independent of every other, in the probabilistic sense described above.

Now that we know a little bit about probability, we can say more precisely how this motion is characteristic of what is called a random walk, or a 'simple' random walk. Sometimes the word 'random walk' is used for more general kinds of walks; in this course we will always take it to mean the following.

(Simple) Random Walk: A sequence of steps, each of which is (1) of equal length; (2) equally likely to be in any possible direction; and (3) probabilistically independent of all the other steps.

Although it is possible to be more formal about this^*, this is all that we need to understand the essential features of a random walk.

What do random walks describe besides drunkards? You've already seen one: the a molecule suspended in liquid is experiencing Brownian motion is a random walk. Considering time in discrete intervals of a hundredth of a second each, we find that the motion of a suspended sugar molecule, or of a fat globule, is described by a random walk. Each step is about the same length, is in an arbitrary direction, and is probabilistically independent of the steps that came before.

Suppose we just restrict attention to two directions, say up and down. Then it's easy to simulate the steps of a random walk, using resources like Wolfram Alpha. It looks like this (click the image to generate more samples):

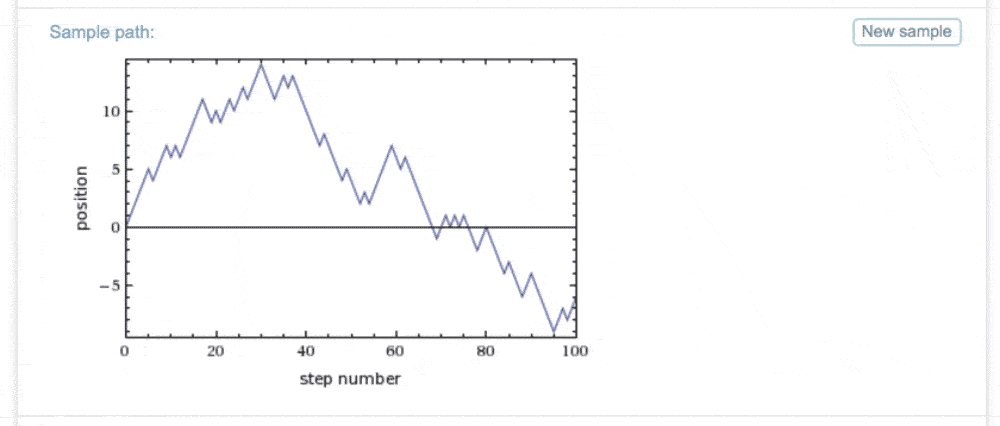
Does this graph look familiar? It should be suggestive; looking ahead to future weeks, we shall see that stock indices can be modelled using random walks, although what exactly should be the "random" part will be a central question. We will return to this later.

Properties of random walks

Of course we can't predict exactly what will happen during a random walk; that's the whole point. The strategy of describing a system in terms of a random walk is a way of embracing our ignorance in order to describe the average behaviour of a system instead. It turns out that when we embrace our ignorance, we can sometimes learn quite a lot.

For example, we can expect for example that the drunkard will on average not make any progress. What we mean by this more precisely is that, if a group of drunkards were to pile out of a pub and all start following a random walk and then collapse after twenty steps, then the majority would be clustered around the door of the pub.

However, we can also expect that that in spite of this, the drunkards will tend to drift farther with time. After a short amount of time the drunkard is unlikely to be far away from the starting point. But as more and more time passes, the likelihood of drifting away from the starting point increases.

In fact, one of the most important results in the theory of statistics, called the Central Limit Theorem, implies the following corollary:

Random Walk Limit Theorem. As the length of time between steps in a random walk becomes small, and the number of random walkers and steps becomes large, the distribution of random walkers in space approaches the normal (or "Gaussian", or "Bell curve") distribution.

You can also check this empirically using a simulation of a random walk, which over time becomes normally distributed.

As a result, if the displacement of each person in a pub follows a random walk, and they start at the black dot below and walk a fixed number of steps, they will become normally distributed. And they will spread out more as they take more steps.

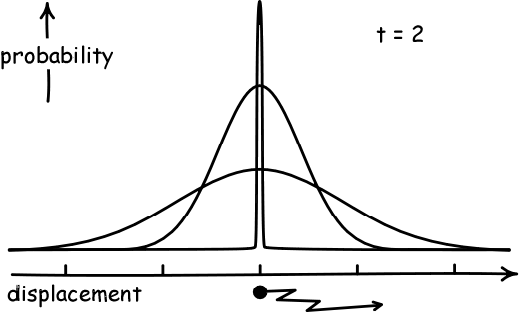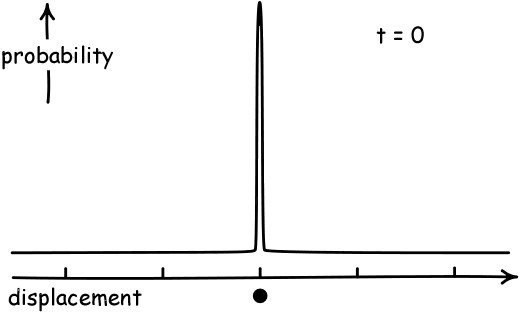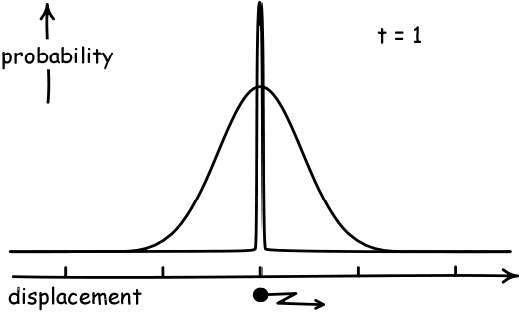
(Image Credit: John D. Norton)

The precise name for the "amount of spread" away from the average that a normal distribution has is called its variance. The variance has a formal definition, but this is not necessarily for our purposes. Our main interest in this course will be the fact that the "spread" or variance of a distribution corresponding to a random walk will increase over time.

When is it a random walk?

If we wish to reasonably describe some system using a random walk, then it must be reasonable to assume the three conditions of a random walk. Although a given motion may look random, that is not enough. To know if it is a random walk, we must check that the three properties above are satisfied.

In the case of the drunkard, the properties of a random walk can be traced largely to the suppression of motor abilities that alcohol causes to the brain. Tiny variations in your body position, as well as environmental factors like the air around you, amount to a barrage of billions of little "pushes" on your body in different directions. These factors have a net effect of pushing you in some direction. Alcohol can inhibit the brain's normal quick counter-acting of these little pushes, and can also effect the inner-ear, which leads the brain to exaggerate its eventual response. But most importantly, one cannot possibly predict the net effect of those tiny variations, and one can expect them to (roughly) be independent from moment to moment. It is to this extent that a drunkard can be said to follow a random walk.

Think about the random walk as a tool. If used correctly, it can be a powerful means of analysis. But like many tools, its incorrect use can lead to disaster. So in general, when you see a random walk appear in a model, be sure you do the exercise of checking whether one may reasonably assume the three conditions!

What kind of thing is this probability?

The concept of probability is a truly remarkable idea. Like magic, it allows us to make predictions about things in spite of our state of ignorance, and with astounding success. Part of the job of philosophy of science is to understand the structure of science and why it works. This leads one to ask, what kind of property is probability?

There are many different answers to this question, each of which is known as an interpretation of probability. Here are a few of them for you to consider.

• Subjective interpretation. A probability represents a human or ideal-human degree of belief in the truth of a proposition (like, "my degree of belief that a coin will land heads is 1/2").
• Relative frequency interpretation. Probability represents the frequency of some class of occurrence relative to some reference class (like, "the frequency of heads-flips is 1/2 relative to the class of all flips".)
• Propensity interpretation. A probability is a tendency or dispositional property for something to an occur (like, "the disposition of the coin to land heads is 1/2".)

There is a great deal of philosophical debate around these questions. For example, the founder of the LSE Philosophy department Karl Popper wrote a classic article presenting the propensity interpretation, with Gilles (2000) describing some alternatives, and van Fraassen (1977) describing relative frequencies and some of their difficulties. Of course, the answer need not be the same in every application of probability. So, something for you to keep in mind as you study probabilistic phenomena in this course is: what does it mean for in this particular description to display probabilistic behaviour? The answer will often be a matter of interesting philosophical debate.