Of Flowers and Fortunes
The Tulip Mania Crash
The dawn of the 17th century marked a period of unprecedented growth in the Netherlands. The Dutch East India company was founded. The world's first stock market was created in Amsterdam. And one industry came to establish itself as one of the surest, safest investments: tulips.

Yes, tulips. This new species with intense colour contrast was imported from the Ottoman Empire, and soon became a household and garden staple in the burgeoning Dutch merchant class. Tulips bulbs took a long time to grow and required special growing conditions, which made them a naturally rare commodity. And demand was steady: from 1554 up through 1634, the tulip industry experienced a continuous and steady expansion. Indeed, tulip industry's expansion was so regular that the industry became the reliable investment of a generation.
In the 1634, the price began to accelerate upward. The tulip fad spread to France increasing demand. Tulip futures contracts started entering the market, which investors jumped on as a way to make quick cash since the profit seemed endless. The bulbs themselves started to sell for incredible prices: some rare tulip bulbs were sold for the equivalent of £10,000.
Then, seemingly out of nowhere, on February 4, 1637, the tulip market crashed.
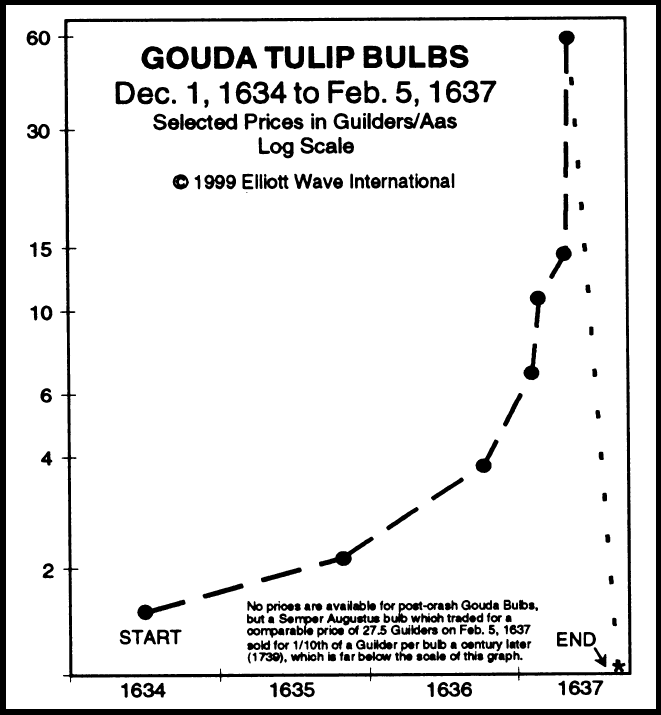
The super-expensive bulbs became worthless. Fortunes were lost. "Tulip Mania", as it came to be called, was over.
Other Famous Crashes
The tulip mania crash was just the first of many famous stock-market crashes. Here are some of the most famous ones.
| The Tulip Mania Crash (1637). Tulip bulb prices grew steadily for over 100 years before dramatically increasing and then crashing. Tulip Mania |
| The South Sea Bubble (1711). The South Sea Company's stock price rapidly inflated and then crashed. |
| Black Tuesday Wall Street Crash (1929). The stock market expansion corresponding to 1920's American industrial expansion crashed dramatically on October 24th (Black Thursday) and again on October 29th, initiating the Great Depression. |
| Stock Market Crash of 1987. The largest one-day crash in history. |
| Japanese Asset Price Bubble Crash (1992). Japanese real-estate and stock prices inflated over a decade and then crashed, plunging Japan into a decade of economic contraction. |
| The Dot-Com Bubble Crash (2000). The new internet economy led to enormous stock price inflation before crashing. |
| The Financial Crisis of 2007-2008. Securities associated with risky mortgage loans increased dramatically and then crashed, leading to a collapse of the banking sector in the United States, followed by the worst financial crisis since 1929. |
What is a market crash?
Events like the Tulip Mania catastrophe are known as "market crashes". Roughly speaking, a market crash is a momentous drop in a financial market or sector. These drops are often far from what is allowed by traditional economic models, involving many dramatic changes in price at once. So, we here again enter territory that goes beyond the classical analysis.

But apart from this basic fact, what kind of thing is a market crash? Is it the result of a single recognisable economic mechanism? Can it be predicted or avoided? These questions are extremely controversial. But we may identify at least three views: the sceptical view, the new information view, and the instability view. We discuss each of them in turn.
The sceptical view of crashes
A reasonable first pass at these questions is to say: no, there is no unified mechanism underpinning stock market crashes, and they cannot in general be predicted. This is the "sceptical hypothesis": one is sceptical of the proposal to develop a science of crashes. After all, crashes tend to be unforeseen by investors, but also especially by economists. For example, exactly 14 days before the Black Tuesday Wall Street crash of 29 October 1929, distinguished Yale economist and statistician Irving Fisher wrote,
"In a few months, I expect to see the stock market much higher than today."

Irving Fisher, Yale economist and failed prognosticator of long-term stock market success
Indeed, things look great before a market crash. Stock markets are on the rise, there is typically strong output and low unemployment, and generally every reason to think the economy is healthy. This sense of optimism in 1929 was so powerful that, a few days after the crash, the Harvard Economic Society told its subscribers,
"A severe depression such as 1920-21 is outside the range of probability. We are not facing a protracted liquidation."
Of course, the Society dramatically failed to predict the Great Depression that followed, and were shuttered a few years later in 1932.
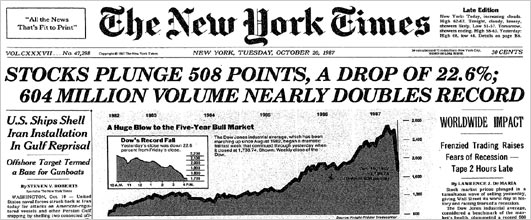
More recently, in response to the 1987 stock market crash, a group of 33 economists predicted that "the next few years could be the most troubled since the 1930's." You can still read the gloomy New York Times report here. The stock market was hardly effected, with growth continuing through 1987, and the Dow Jones returning to its pre-crash average value by early 1989.
Such pronouncements do not give one confidence in the ability of scientists to understand the mechanisms underpinning market crashes. But it remains worth exploring whether we might be able to do better than skepticism.
The New Information view
The more traditional perspective on market crashes for economists is that they are surprise downturns revealed only by a new crucial piece of information. For example, the Chicago economist Allan Kleidon writes,
"price changes can only occur if some new external information reaches the market as a whole. Price changes, including crashes, are caused by new information about fundamentals within a framework of rational expectations." (Kleidon 1995)
Stock market crashes consist in an incredibly complex collection of interconnect events, each of which is of which is highly unpredictable. For example, here is a sampling of some of the reasons commonly given to explain the October 1929 Wall Street crash.
- Production outran consumption. With the advent of the assembly line and other manufacturing advances, industrial products like cars and steel grew faster than consumer demand could keep up. The US Federal Reserve indexes of industrial activity peaked in June before the crash, and then proceeded to follow a steady decline.
- Agricultural recession. The agricultural industry had been struggling for some time before 1929. The many small rural banks that were sustained by this industry were thus already weakened when the crisis hit.
- Irrational optimism. As with a gold rush, a great number of people became irrationally convinced that the stock market was a quick way to get rich. This led to a great deal of novice speculation, which made the market unstable.
Each of these phenomena would be difficult to predict on its own, and their exact effect of their conjunction on the economy even more difficult to predict. This is especially the case when other factors like strong employment and growth rates indicate that the economy is strong.
That the mechanism behind stock market crashes is difficult or impossible to predict is a natural corollary of the random walk perspective on markets. Since changes in the market are independent of past behaviour, a market crash is in principle impossible to predict. They can at best be caused by the sudden revelation of new information, in which case it is already too late.

This paradigm is so ingrained that in most post-hoc explanations of a market crash, the discussion is always about what the fateful piece of information was that caused the crash. The cause identified is usually something that took place days or even hours before the event. However, there is rarely agreement about what the relevant information is, and it is pessimistic about the possibility of predicting a crash.
The instability view
Many market crashes share some common characteristics, which has led to a perspective which may be called the "unstable buildup" view. On this perspective, market crashes happen when securities undergo a particular kind of rapid growth over a period of weeks, months, or even years. Like the growth of snow on a hillside after a heavy snowfall, this is an unstable state for the market to be in. Like a snowy hillside, a market in an unstable state can come crashing down at any moment. And like an avalanche, it is sometimes possible to identify the danger, even if you can't predict what the trigger will be.

An avalanche is the result of an unstable buildup. It is usually difficult to predict what exactly will cause an avalanche, but easy to predict that one is likely to happen.
This is a completely different paradigm. On this view, one goes beyond the sceptical perspective, and does not try to say anything about the particular cause of a stock market crash. One only tried to predict when the conditions will be sufficiently unstable for it to happen.

Crashes often occur after an upswing in interest in some security like stocks, coins, or commodities. The crowd's interest in the item is thought to become self-compounding, with the growth of the item itself feeding more growth, which gives rise to a super-fast growth rate. For example, the upswings in the stock market around the time of the October 1929 Wall Street crash were followed by upswings in book sales on stocks, suggesting some kind of "herd" behaviour was involved.
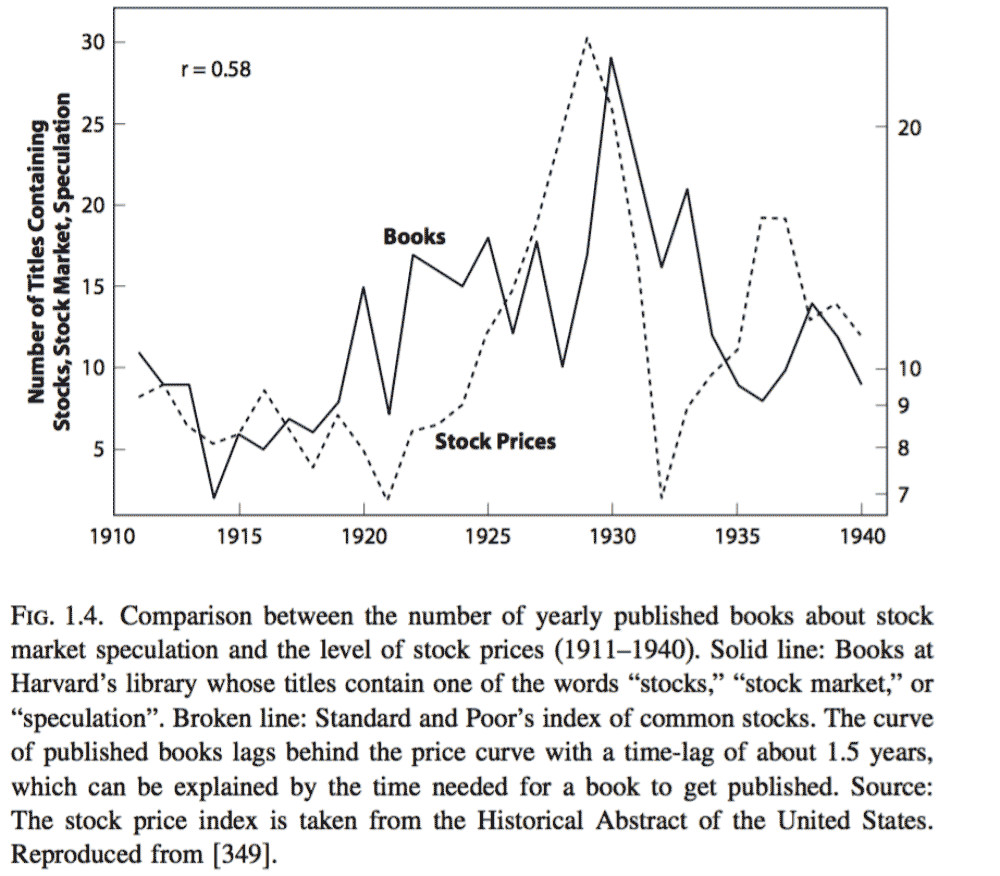
Correlation between S&P price and numbers of books checked out about stocks and speculation is evidence for "herd" behaviour.
This view has been advocated in recent years by Didier Sornette and his colleagues. It is known as the log-periodic power law approach to stock market crashes. And it provides some of the most remarkable insight into stock market crashes ever developed.
The Log-Periodic Power Law model
Herd behaviour
Herd behaviour occurs when many participants act in the same way at once, pushing the group rapidly in some general direction.

Group behaviour associated with rapid growth is familiar in modern internet culture. For example, it is responsible for the phenomenon of viral videos and memes. At some point it is not just the original item but the crowd's interest itself begins to fuel its own growth. When this happens it results in a meteoric rise, which is usually followed by a long decline.
Are financial markets like viral internet memes? The first image below shows the spot price of gold price of gold during the 1979 rise and crash. The second image shows the Youtube viewing statistics for the viral video and most-watched video on YouTube, "Gangnam Style" by Psy. The similarities between the gold and Gangnam style curves are remarkable.
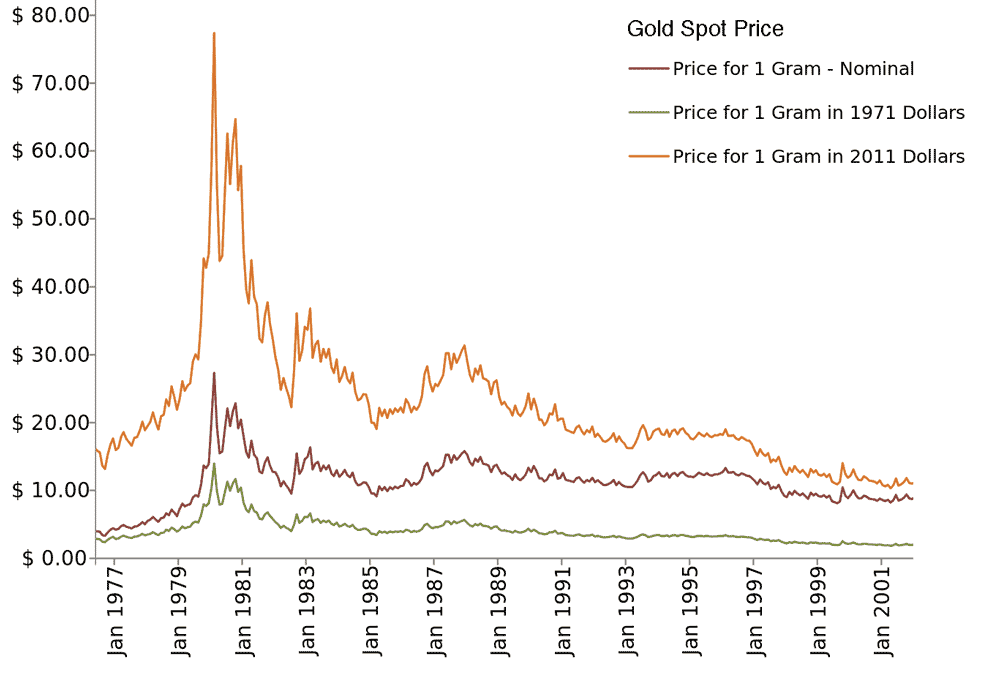
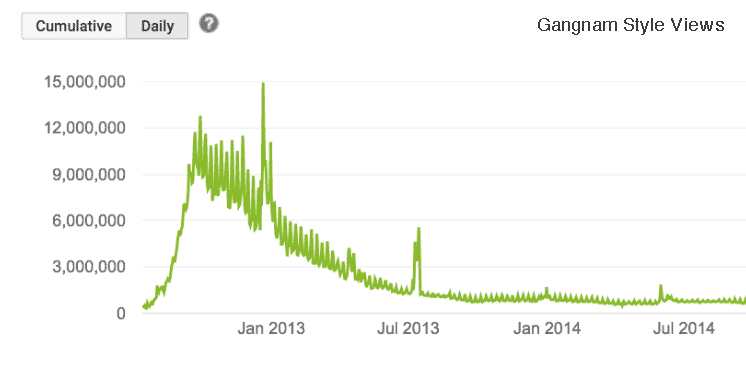
Herd behaviour tends to be marked by choices that are made not because they are rational, but because everybody else is doing it. This has long been a warning-flag to investors.
For example, John F. Kennedy's father Joseph Kennedy pulled all of his investments out of the stock market just before October 1929 and walked away with millions. He later claimed that he had inferred the market was in a speculative bubble. But the only evidence he cited was that he had heard a shoe-shine boy offering market tips. Perhaps this shoe-shine test is a reliable predictor; more likely is that Mr. Kennedy had the good fortune of encountering some substantial good luck.

From herds to bubbles
When a balloon swells up, it becomes very sensitive to its surroundings. A pin-prick or even a turbulent gust of air can be enough to destroy an over-inflated balloon. When someone pricks the balloon, there is some sense in which they cause the bubble to burst. But there is another sense in which the bubble was already in an unstable state, ready to burst from any of a number of possible triggers.

Many phenomena can be described in a similar way: avalanches, earthquakes, childbirth, and stock market crashes. They are all characterised by a fast-growth period, followed by a period of instability, followed by a crash. The instability view then suggests that to predict such critical vents with decent accuracy, it is sufficient to predict the occurrence of a period of instability.
The basic mechanism for this is the assumption that there are two kinds of investors: rational investors and "herd" investors. The latter group is taken to be an irrational, trend-following group that imitates the trend and generates extremely rapid growth. When a critical event occurs, many investors are then at once inclined to sell, which gives rise to a market crash. Such events are only guaranteed in the model with a certain probability. As a consequence, it is often rational for investors to continue investing, since the bubble may push the expected value of an investment high enough up so as to seemingly compensate for the danger of a crash.
If we agree that the particular critical event might be completely unpredictable, a question remains as to then whether it is possible to predict oncoming instability associated with a bubble. Some argue that it is.
The Log-periodic power law growth signal
In September of 1997 Didier Sornette was a physicists working on earthquakes in the geology department at UCLA. That month, Sornette correctly predicted the October 1997 market crash that brought down the Asian housing market and ultimately Long Term Capital Management, the investment group that Scholes and Merton were working for. He also managed to predict the US real-estate bubble before it happened. Indeed, Sornette has made a great number of predictions about economic downturns, all drawing on the instability approach to stock-market crashes.
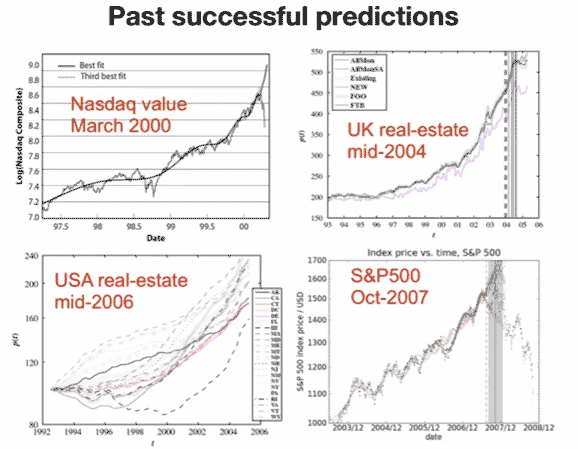
The basic prediction of Sornette's model is that stock market crashes are associated with an instability in the market that can be identified by three basic features.
- (log): Eventually undefined prices, for which the model simply breaks down and stops making a prediction about after finite time; this point is called a critical time.
- (periodic): Oscillating prices that jump up and down with a regular period as they approach the critical time.
- (power law): Super-exponential price growth, described by functions like \(x^{x^2}\) that grow faster than an ordinary exponential.
Sornette captures these features in a single model of price growth called the log-periodic power law. The "log" and "power law" refer to the feature of a function that describes the super-exponential growth, as well as the undefined "singularity". They give rise to a change in price (y-axis) over time (x-axis) that looks like the following.
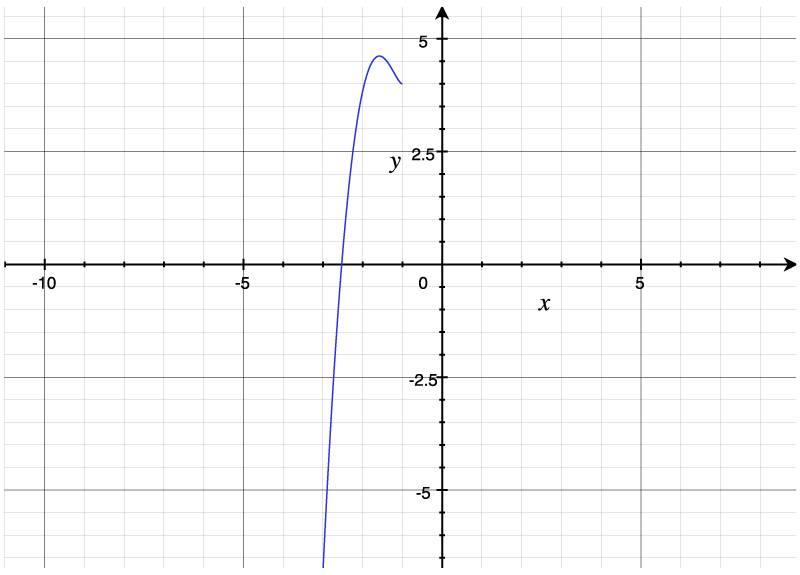
A log power law without the periodicity
With the added assumption of "periodicity" we get the full log-periodic power law, which oscillates towards a singularity at a super-exponential growth rate:
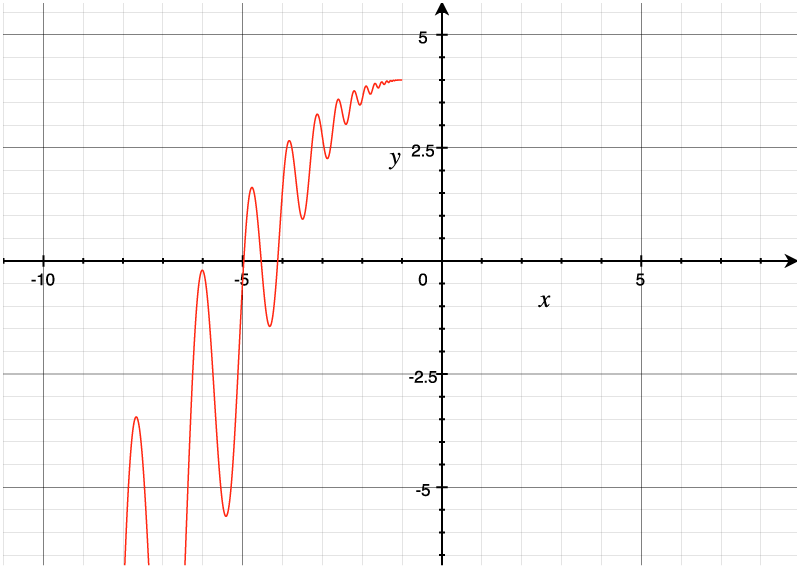
A log-periodic power law: the same as the log power law above, but with oscillations added.
Optional: Mathematical form of the log-periodic power law
Sornette's simple idea is that if a price is following a log-periodic power law, then approaching the critical time indicates increasing instability, during which time a crash is very likely. So, to predict a crash of a security or market, one only has to try to fit the price to a log-periodic power law, and then just calculate the critical time. This will tell you when a market crash is likely. For example, Sornette carries out this exercise to predict the HK and S&P 500 crashes in the plot below.
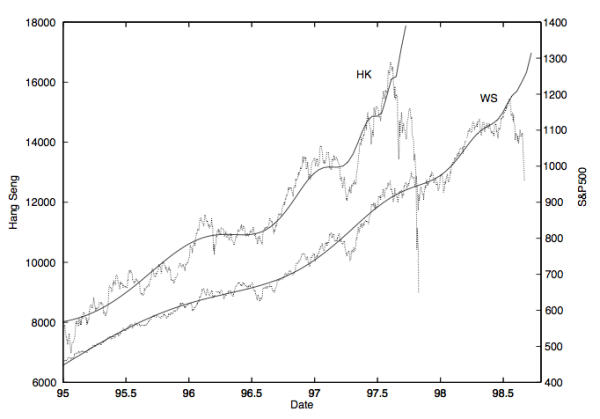
Fitting a log-periodic power law curve to market indices allows one to predict a crash. Notice the downturn during the period of instability as one approaches the critical time. From Sornette (2003).
Sornette has achieved considerable success with this kind of thinking, so much so that the predictions of his research group are often encrypted to avoid crashing the market just by their announcements. You can watch a recent Ted talk featuring Sornette discussing his theory in stylised terms below.
Are there laws of finance?
Many sciences are characterised by laws of nature: physics has Schrödinger evolution, the Born rule, and the Einstein equation for gravity. Biology has the laws of evolution by natural selection. And many social sciences use the word 'law', from 'Malthus's Law' to the 'law of supply and demand'.
And yet, unlike the natural sciences, it remains highly controversial whether there are laws in the social sciences, and in particular in finance. For example, we have discussed Donald MacKenzie's suggestion that the phenomenon of performativity gives rise to a certain kind of lawlessness in finance.
However, performativity does not imply lawlessness. For example, we have now seen that the herd-behaviour of the markets can be described in precise or even "law-like" terms, using instability models like the log-periodic power law. To some extent, the herds can be tamed.

Against hedged laws
John Roberts (2001) has argued on more general grounds that there are no laws in the social sciences. Roberts focuses on the fact that laws in the social sciences tend to admit exceptions. For example, the Black-Scholes model only applies if there is no arbitrage. The Osborne log-normal distribution applies for equal step-sizes. Let us say that a financial law that admits exceptions of this kind is called hedged. It is describing some regular behaviour of the financial world, but only subject to some exceptions.
The position of John Roberts is that such systems are not worthy of being called laws. His argument can be summarised as follows.
- If there are any social laws, then they are hedged laws.
- There are no truly hedged laws.
- Therefore, there are no social laws.
His first premise generalises a common feature of the financial models that we have studied: they only hold under particular circumstances. In this sense, financial laws (and perhaps all laws governing social systems) are hedged, often by giving an explicit list of exceptions.
Why does he say that hedged laws are not worthy of the title "law"? The argument that Roberts gives is that hedged laws tend to either be vacuous, or lead to unfalsifiability. In the first place, if hedged laws are said to be "true, except when they are not", then this is a simple logical tautology and hardly worthy of the title "law". On the other hand, if we are allowed to give a list of exceptions, then whenever a falsifying instance of the law is found we can just add it to the list of exceptions, and in this way always avoid falsifying the law.
If Roberts is right about this, then none of the models we have seen so far are laws, since they are hedged. The suggestion is that in contrast, the laws of physics are not in general hedged.
Are hedged laws unique to finance?
A remaining question is: does the sort of hedging required to formulate financial laws make them qualitatively different than the laws of physics? This is not so clear. For example, we saw in Lecture 4 that quantum mechanics admits two laws describing the future state of a system, the Born rule and Schrödinger evolution. Each one is hedged to accommodate the other. Worse, we currently have only heuristic tools for determining which one is appropriate, and each one must be hedged in order to accommodate the other. Is this radically different than the kind of hedging we do in finance?
Many other reliable laws of physics are hedged. For example, the ideal gas law breaks down when there are strong interactions between the particles, which ruin the independence assumption in the random walk hypothesis. Indeed, Osborne's log-normal model and the ideal gas law draw on such similar arguments, it seems they succeed and fail for many of the same sorts of reasons. Moreover, the Schrödinger equation is often said to break down when a measurement occurs and the Born rule must be used. Thus, it appears that many of our best examples of laws in physics are subject to a similar complaint.
In the second place, it is not obvious that hedging leads to unfalsifiability. For example, the log-normal power law model of market crashes has been extensively tested, and in some cases revised and improved when it was found wanting. Similarly, the Black-Scholes equation has been subject to a wide variety of tests. When falsifying instances are found, one often seeks to improve the law rather than just accumulate a list of exceptions.
The question of the differences between laws in physics and in finance appears to be considerably more subtle. Performativity is certainly a unique feature of finance, but this does not appear to prevent one from formulating laws of finance, but rather requires that they take a particular form. Much philosophical work on this topic remains to be done. However, for now I leave the task of pursuing such work to you.

