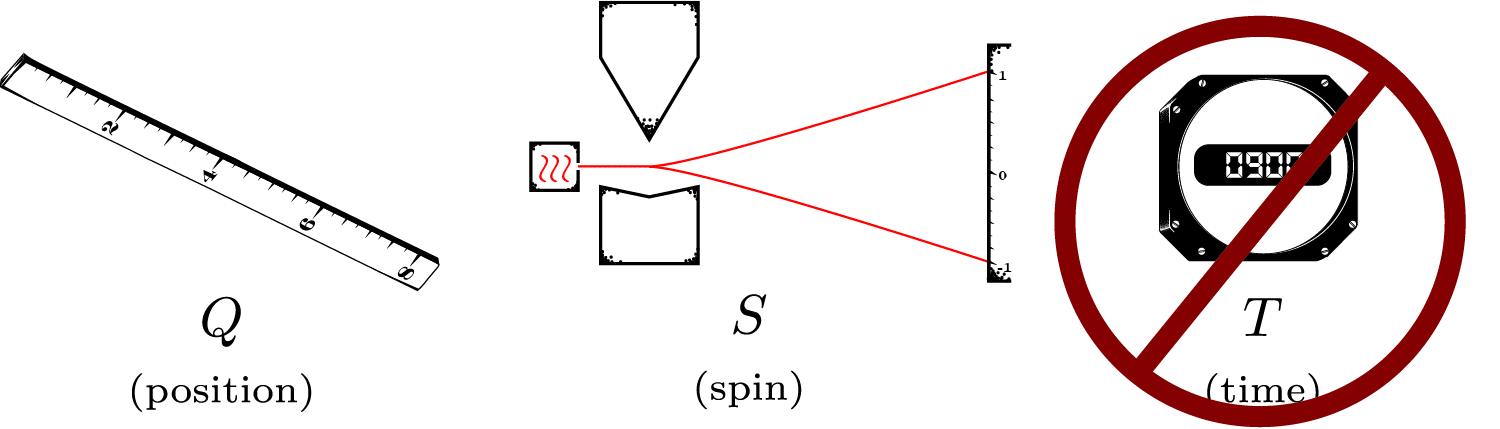
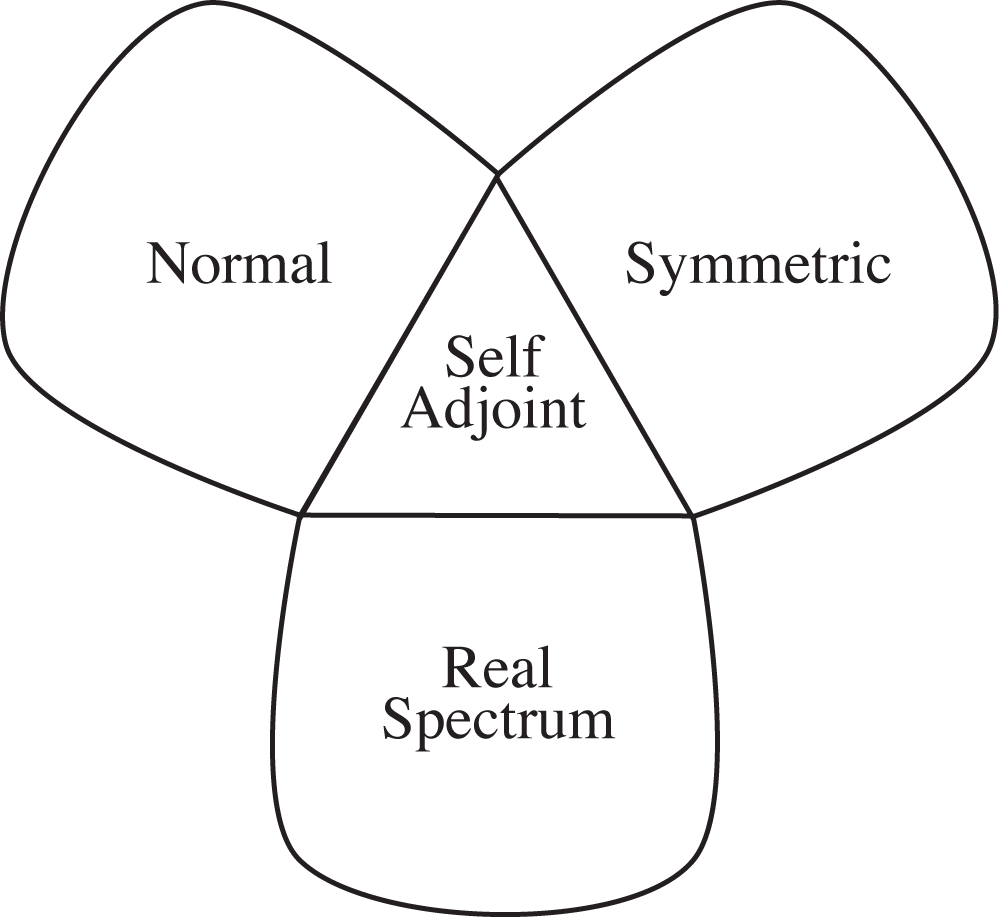
Observables

Disassembled

Paris | 21 June 2018

Bryan W. Roberts
London School of Economics
philsci-archive.pitt.edu/14449

Warm-Up Exercise

Primitive labels

Real-number labels

Real-plane labels

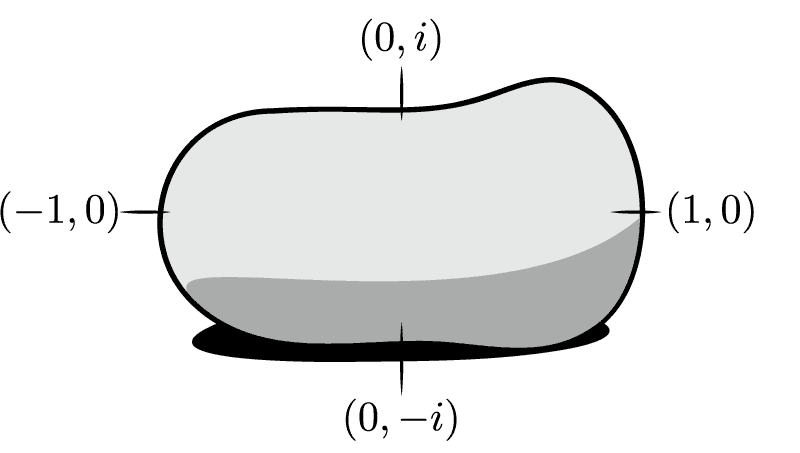
Complex-plane labels

Negative numbers: Initial Skepticism

Negative numbers can represent the world

Imaginary numbers: Initial Skepticism

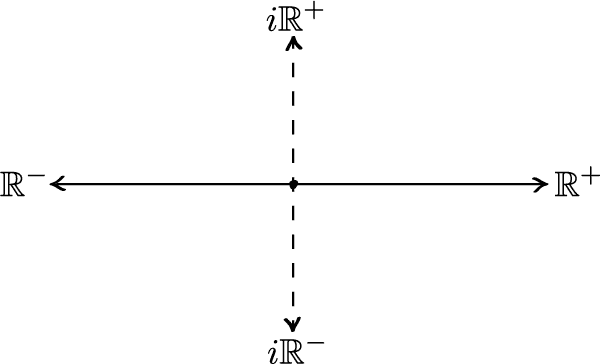
Imaginary numbers can represent the world

"There is no representation except in the sense that some things are used, made, or taken, to represent some things as thus and so."

— van Fraassen 2008, Scientific Representation, pg.23

Some things represented by complex numbers 'thus and so'

Classical waves
Oscillating current
Polynomial roots

MEANWHILE, in modern quantum theory...

Textbook dogma

"Now, the expectation value of an observable quantity has got to be a real number (after all, it corresponds to actual measurements in the laboratory, using rulers and clocks and meters)"

Griffiths (1995), Introduction to Quantum Mechanics, §3.3

Textbook dogma

"We expect on physical grounds that an observable has real eigenvalues.... That is why we talk about Hermitian observables in quantum mechanics."

Sakurai (1994), Modern Quantum Mechanics, §1.3

Philosophical tradition

Identifying the textbook dogma...

"the standard textbook way [to interpret quantum theory] is to associate measurements with certain self-adjoint operators" — Wallace (2012) The Emergent Multiverse

Philosophical tradition

Following the textbook dogma...

"it's clear... (since, of course, the values of physically measurable quantities are always real numbers) that the operators associated with measurable properties must necessarily be Hermitian operators."

Albert (1992) Quantum mechanics and experience

"The analogy with classical [Fourier] theory leads further to allowing as representatives of real quantities only those matrices that are 'Hermitian'" — Born and Heisenberg, Report for the 1927 Solvay Conference

Born and Heisenberg, Report for the 1927 Solvay Conference, drawing on Born, Heisenberg and Jordan (1925) "QM II"

Classical Harmonic Analysis
\(\psi(x,t) = A\cos(z)\), with \(z := \tfrac{2\pi}{\lambda}(x - vt).\)

Convenient for calculations: \(Ae^{iz} = A\cos(z) + iA\sin(z)\)

To make predictions: \(\mathrm{Re}\left(Ae^{iz}\right) = A\cos(z)\)

"These assumptions are reasonable on account of the eigenvalues of real [Hermitian] linear operators being always real numbers." — (Dirac 1930, Quantum Mechanics, pg. 35 of 3rd/4th edition)

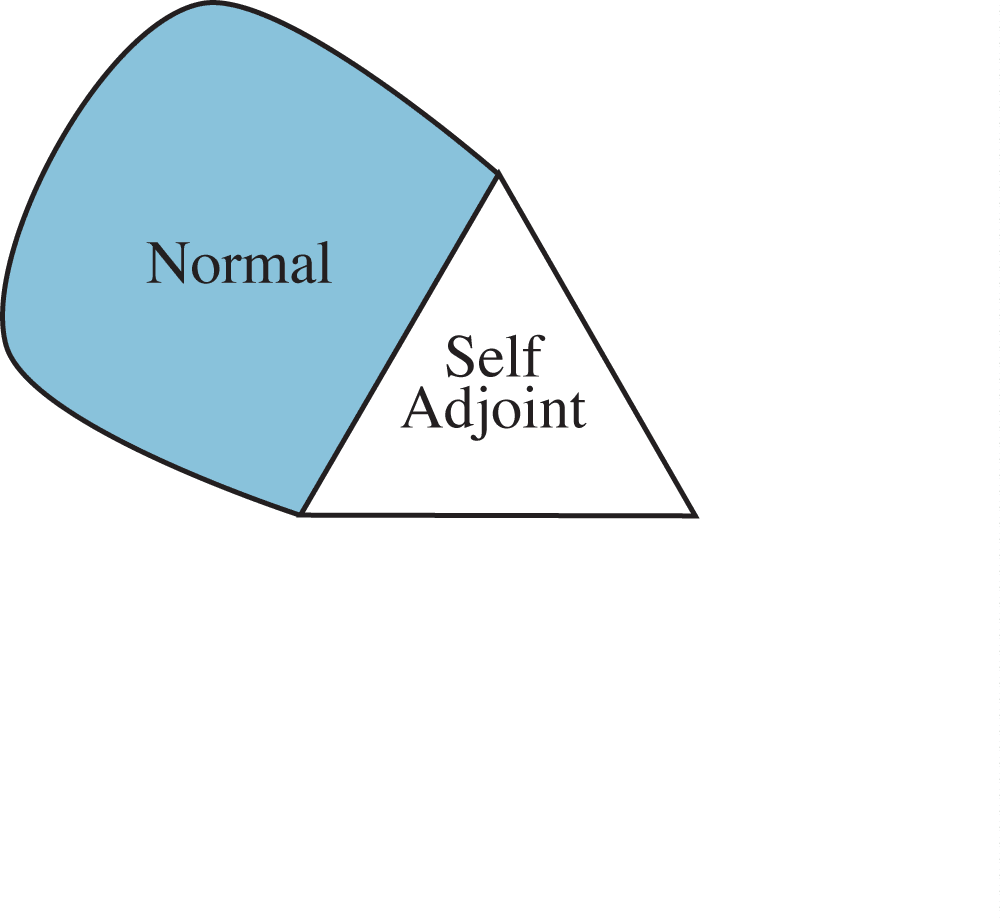
Thesis:

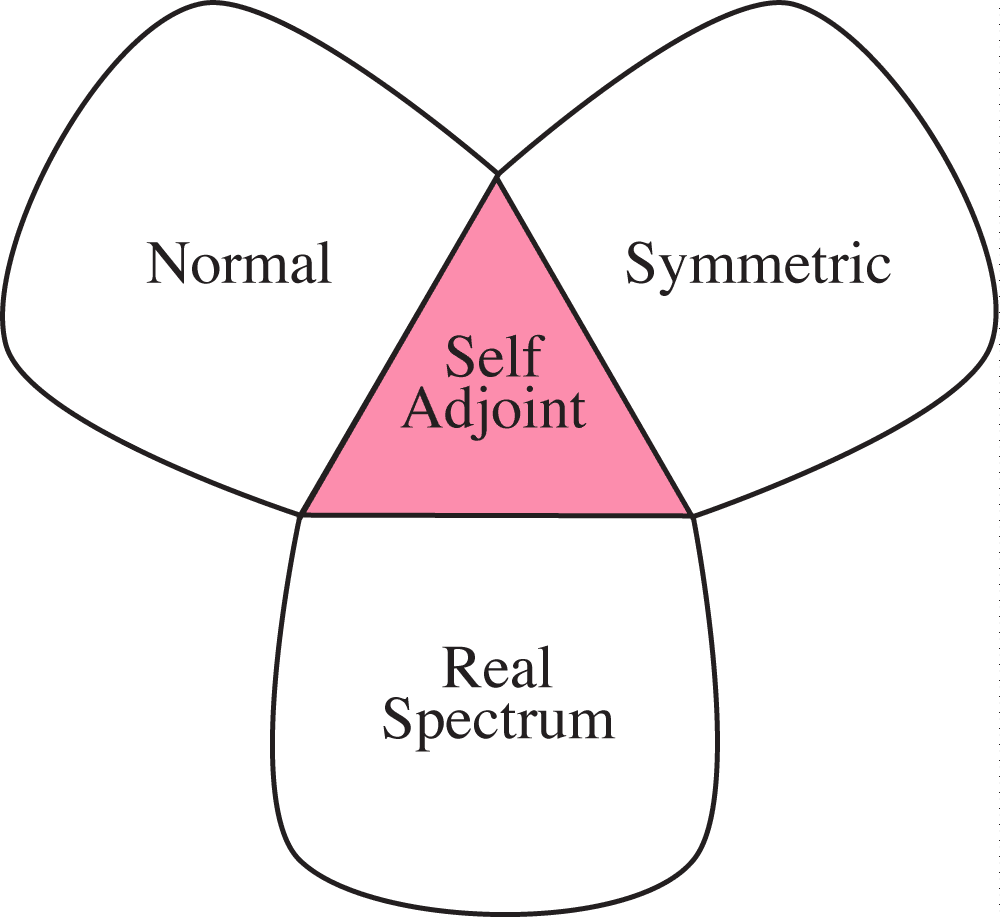
The standard dogma that observables must be self-adjoint (with real spectrum) should be relaxed.

The reward: New interpretive questions, new symmetries, and new physics.

Observables: a Disassembly Theorem

\[ A^*\psi = A\psi, \;\;\; D_A = D_{A^*} \]

Observables: a Disassembly Theorem

\[ A^*\psi = A\psi \]

Observables: a Disassembly Theorem

\[\mathrm{spectrum}(A)\subseteq\mathbb{R}\]

Observables: a Disassembly Theorem

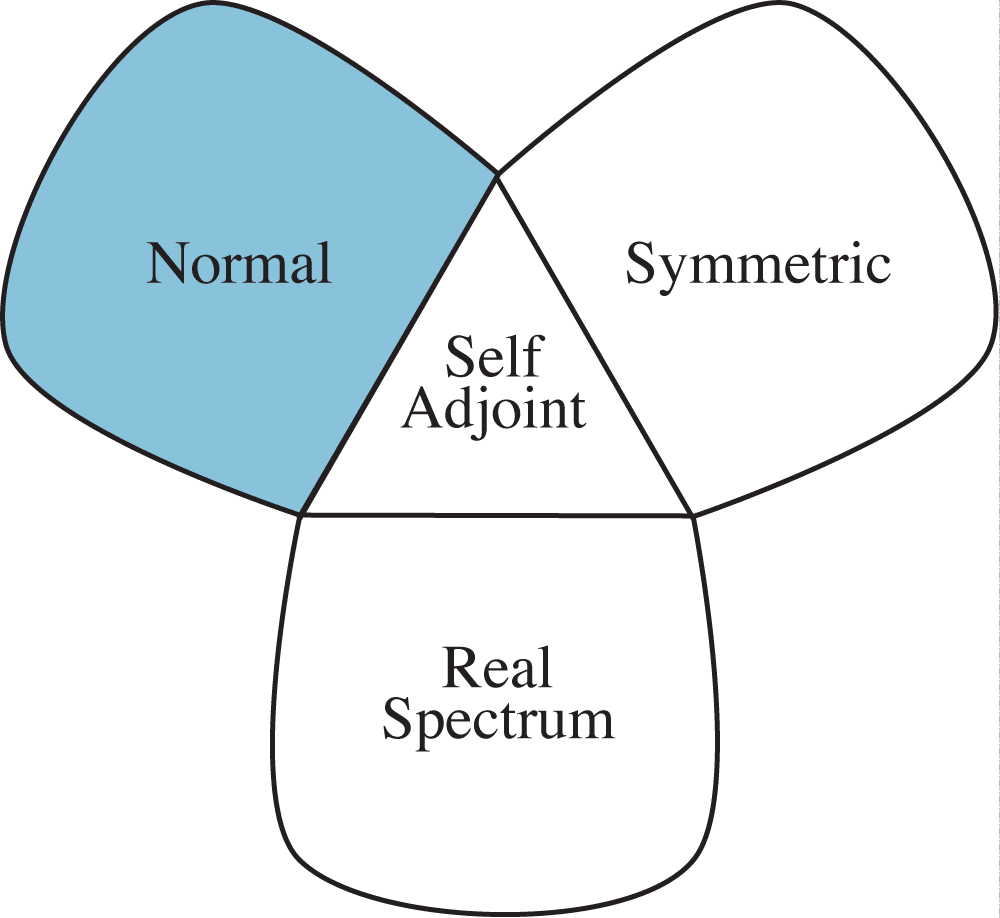\[ AA^*=A^*A \]

Eigenvalue Equation

\[ \sigma\varphi = a\varphi. \]

Eigenvector \(\varphi\) of an matrix \(\sigma\) with eigenvalue \(a\):

Self-adjoint spin observable \(\sigma_z = \bigl(\begin{smallmatrix}1 & \\ & -1 \end{smallmatrix}\bigr)\)

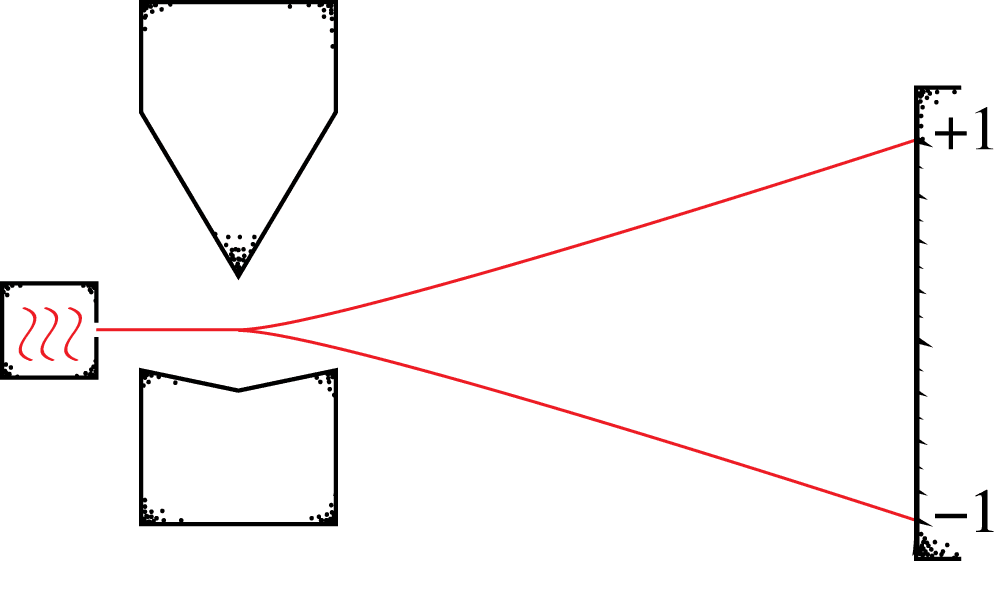
Eigenvectors \(\varphi^\uparrow,\varphi^\downarrow\), Eigenvalues \(\pm 1\)

Non-self-adjoint spin observable \(i\sigma_z = \bigl(\begin{smallmatrix}i & \\ & -i \end{smallmatrix}\bigr)\)

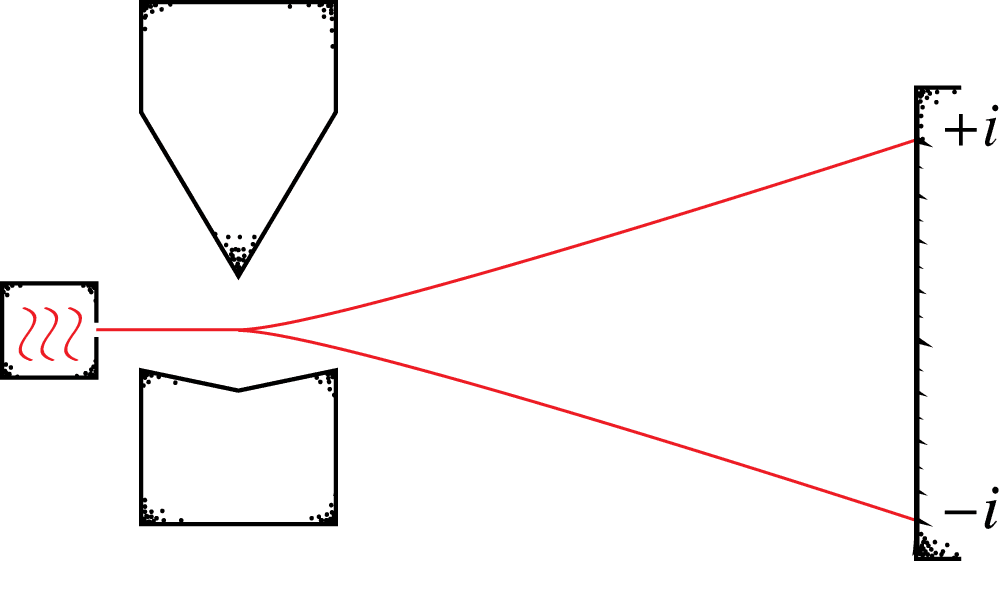
Same Eigenvectors \(\varphi^\uparrow,\varphi^\downarrow\), Eigenvalues: \(\pm i\)

Call \(i\sigma_z\) an unreal observable.

Can we use it to do physics?

We can assign probabilities as usual:

\[\Pr\textstyle_\psi(\varphi^\uparrow) = |\langle \varphi^\uparrow, \psi \rangle|^2 \]

These depend on eigenvectors, not eigenvalues.

...and expectation values as usual,

\[ \langle\psi,A\psi\rangle = i\Pr\textstyle_\psi(\varphi^\uparrow) + (-i)\Pr\textstyle_\psi(\varphi^\downarrow) \]

As expected, it is a complex number!

Why this works. Normal operators have a spectral resolution, which guarantees well-behaved probabilities.

For \(A\) self-adjoint (\(A=A^*)\),
the spectral theorem implies well-behaved probabilities:

\[ \Pr\textstyle_\psi(\varphi_1) + \Pr\textstyle_\psi(\varphi_2) + \cdots + \Pr\textstyle_\psi(\varphi_n) = 1 \]

For \(A\) normal (\(AA^*=A^*A)\),
the spectral theorem still holds:

\[ \Pr\textstyle_\psi(\varphi_1) + \Pr\textstyle_\psi(\varphi_2) + \cdots + \Pr\textstyle_\psi(\varphi_n) = 1 \]

"All... operators do not possess a complete, orthonormal set of eigenfunctions. However, the Hermitian operators capable of representing physical quantities possess such a set. For this reason we give the name 'observable' to such operators."

Messiah (1961) Quantum Mechanics (Vol 1, Ch.V.9)

But the same applies to normal operators too!

Normal operators (\(AA^*=A^*A\)) can be observables.

self-adjoint	\(Q, \; \sigma_z\)
anti-Hermitian	\(iQ, \; i\sigma_z\)
unitary	\(e^{-itH}\)
other functions	\(f(Q), \; g(\sigma_z)\)
\(\vdots\)	\(\vdots\)

Heterodoxy

"I am happy for the results of measurements (eigenvalues) to be complex numbers, while insisting on the standard requirement of orthogonality between the alternative states that can result from a measurement, I shall demand only that my quantum 'observables' be normal linear operators"

— Roger Penrose (2004), Road to Reality

Heterodoxy

Jordan's early (1926) formalism for matrix mechanics suggests treating normal operators as observables.

Duncan and Janssen (2013),
"(Never) Mind your p's and q's"

Warning

It turns out that not all normal operators can be considered observables at once.

Sharp sets

Observables: \(\sigma_x, \sigma_y, \sigma_z\)

Observables: \(i\sigma_x, i\sigma_y, i\sigma_z\)

Unobservables in quantum theory

\(|\uparrow\rangle_x = \tfrac{1}{\sqrt{2}}(|\uparrow\rangle_y + |\downarrow\rangle_y)\)

\(\sigma_x\sigma_y\) or 'Joint spin-\(x\) and spin-\(y\)' is unobservable

Unobservables in quantum theory

Fact: \(\sigma_x\sigma_y = i\sigma_z\).

So, if \(\sigma_x\) and \(\sigma_y\) are observables,
then \(i\sigma_z\) is unobservable!

But \(i\sigma_z\) can still be interpreted as an observable...

Just not at the same time as \(\sigma_x\) and \(\sigma_y\)

Definition. A sharp set of operators \(S\) is one such that if \(A,B,AB\in S\), then \([A,B] = 0\).

"A sharp set contains no products of incompatibles"

Such products are unobservables in quantum theory.

\(S = \{\sigma_x, \sigma_y, \sigma_z\}\) is a sharp set.
\(S' = \{i\sigma_x, i\sigma_y, i\sigma_z\}\) is a sharp set too.
\(S\cup S'\) is not a sharp set, since \(i\sigma_z = \sigma_x\sigma_y\).

What I know about sharp sets

...and more things that I want to know!

Proposition 1. The normal operators in \(B(\mathcal{H})\) are not a sharp set.

Proposition 2. Every set of self-adjoint operators is sharp.

Proposition 3. The set \(SA\) of all self-adjoint operators is not a maximal sharp set.

Why? Because \(SA\cup\{cI \;|\; c\in\mathbb{C}\}\) is sharp.

Implications for Observability: There may be more observables than we think there are.

Q1: What is the maximal Bell correlation for sharp sets of normal operators? (Is it different from \(2\sqrt{2}\)?)
Q2: Can 'observables' like AB-phase or Berry-phase be modeled using sharp sets?
Q3: What else are we missing?

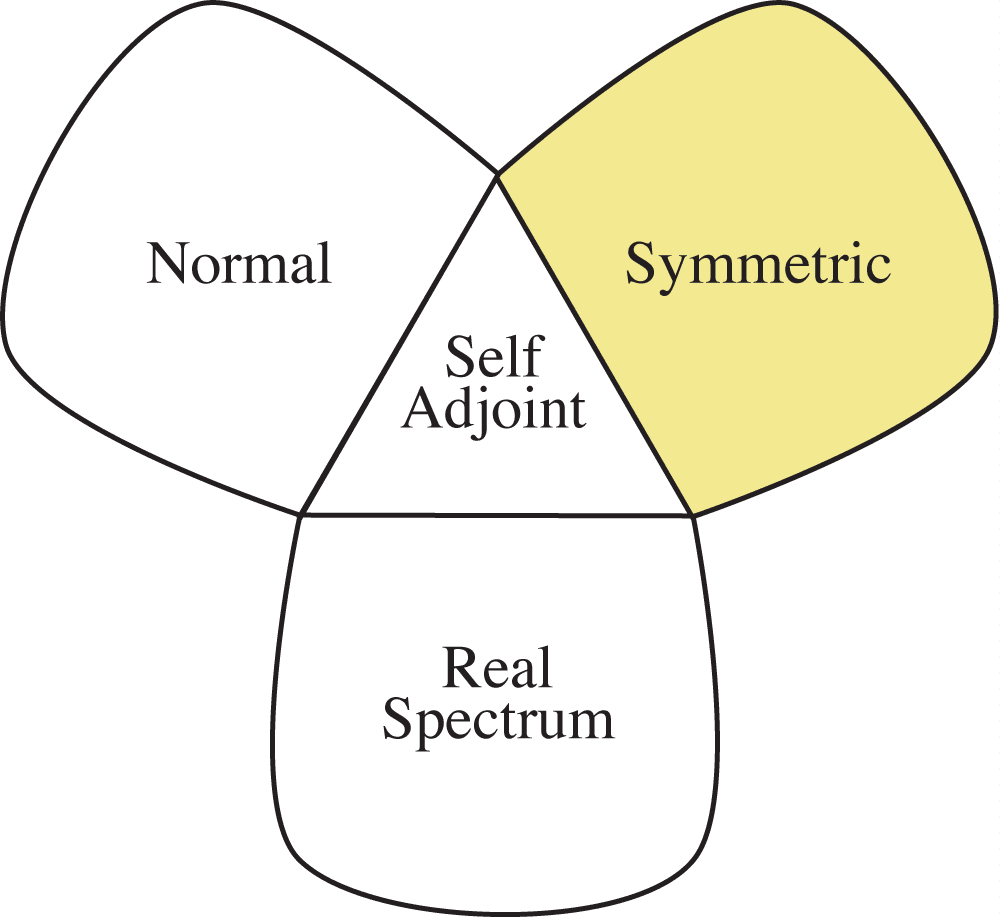
2. Symmetric Observables (\(A\psi=A^*\psi\)):

extension of orthodox Quantum Theory

Adjoint of an operator \(A\) is an operator \(A^*\) such that \( \langle \psi, A\phi \rangle = \langle A^*\psi,\phi\rangle\) for all \(\psi,\phi\in D_A\).
Symmetric operator \(A\) is one such that \( \langle \psi, A\phi \rangle = \langle A\psi,\phi\rangle\) for all \(\psi,\phi\in D_A\).
Self-adjoint operator \(A\) is a symmetric operator such that \(D_A = D_{A^*}\).

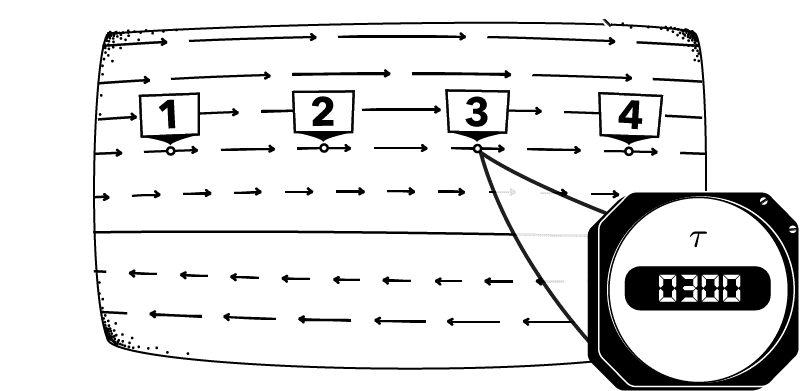
Example: Time observables 'track time' in a dynamical theory

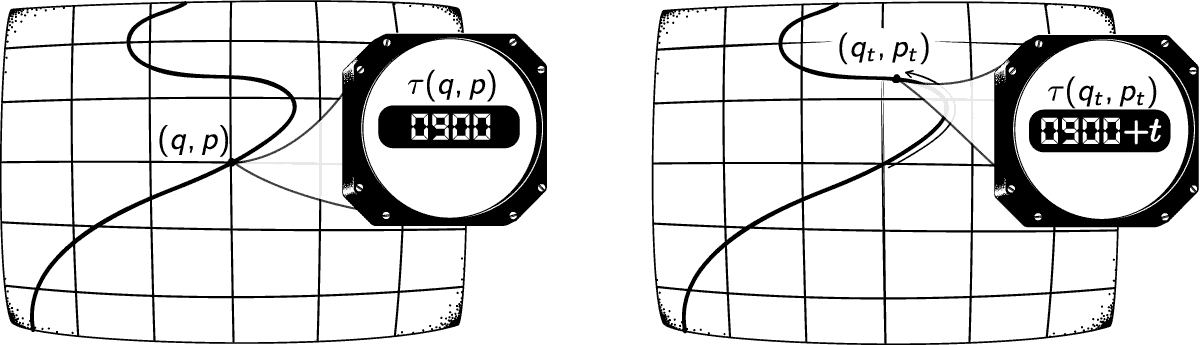
Classical mechanics: \(\tau(s_t) = \tau(s_0)+t\)

Time observables 'track time' in a dynamical theory

Schrödinger QM: \(\mathrm{Tr}(T\rho_t) = \mathrm{Tr}(T\rho_0) + t\)
Heisenberg QM: \(T(t) = T(0) + tI\)

Why 'track time': physics reason.
Predicting the occurrence of a jet

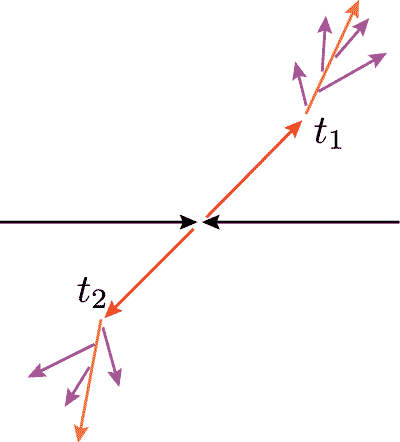
Why 'track time': philosophy reason.
We have measuring devices for it

Energy bounded from below

Energy unbounded from below (implausible)

Pauli's Theorem.
Let \(H\) be a self-adjoint operator ('energy') that is bounded from below.

If \(T\) is self-adjoint, then it is not a time observable.

Pauli's Theorem (Contrapositive).
Let \(H\) be a self-adjoint operator ('energy') that is bounded from below.

If \(T\) is a time observable, then it it is not self-adjoint.

Fact: A huge class of physical systems admit symmetric, non-self-adjoint time observables. (Muga et al 2011, Pashby 2014)

Classical Example: The free particle

\(h(q,p) = p^2/2m,\;\; \tau(q,p) = mq/p\)
\(\Rightarrow \{h,\tau\}=1\).

Quantum Example: The free particle

\[ T := \tfrac{m}{2}(QP^{-1} + P^{-1}Q) \]

Time observable: \([H,T]=i\) when \(H=P^2/2m\)
Symmetric, obviously
Not self-adjoint: \(D_T \neq D_{T^*}\)

Naimark spectral theorem. Every symmetric operator that \(A\) that is closed and densely defined admits a POVM \(\Delta\mapsto E_\Delta\) such that \(A=\int_\mathbb{R}\lambda dE_\lambda\). (It is a PVM iff \(A\) is self-adjoint.)

(Dubin and Hennings 1990, Quantum mechanics, algebras and distributions)

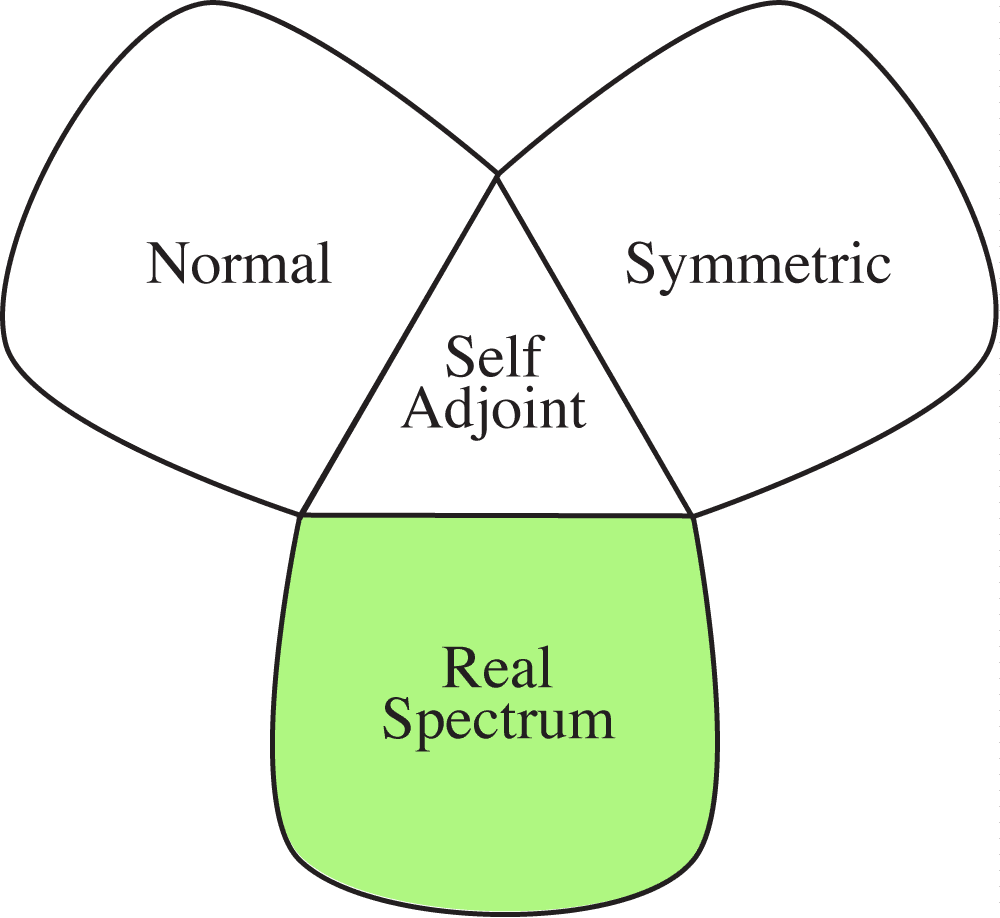
3. Real spectrum Observables:

extension of orthodox Quantum Theory

Example: The operator,

\[ \begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix} \]

has only real eigenvalues \(\lambda=1,2\)

with eigenvectors \(\bigl(\begin{smallmatrix}1 \\ 1 \end{smallmatrix}\bigr)\) and \(\bigl(\begin{smallmatrix}1 \\ 0 \end{smallmatrix}\bigr)\).

But it is not self-adjoint.

Example: The operator,

\[H = \tfrac{1}{2m}P^2 + Q^2 + iQ^3\]

has an entirely real spectrum.

But it is not self-adjoint.

PT-Symmetric Quantum Mechanics explores techniques for constructing such operators, and is of interest in supersymmetric extensions of QM.

(Bender and Boettcher 2000, Dorey et al. 2001)

philsci-archive.pitt.edu/12478/

Thank you.

Appendix

Symmetry Structure

Momentum generates spatial translation

Angular momentum generates spatial rotation

In orthodox quantum mechanics these symmetries \(U_a\) are strongly continuous 1-parameter unitary representations of \((\mathbb{R},+)\).

Stone's theorem: Then \(U_a = e^{isA}\) and \(A\) is self-adjoint.

Stone's theorem \(\Rightarrow\) observables are self-adjoint?

Not convincing.

Observables can generate symmetries, but there is no a priori reason that they must.
\(iA\) is the generator of \(U_a = e^{s(iA)}\). Why promote the part that is self-adjoint?

General Stone's theorem

If \(U_a\) is a strongly continuous 1-parameter unitary semigroup, then \(U_a = e^{iaB}\), and the generator \(B\) is normal.
If \(B\) is normal, then \(U_a = e^{iaB}\) is a strongly-continuous 1-parameter semigroup.

Definition: An unreal observable is a linear operator that is not self-adjoint, but is still used to represent a measurable quantity.

Signaling

Euan Squires (1988) `Non-self-adjoint observables':

"faster-than-light signalling is an inevitable consequence of the assumption that 'measurements'... of non-self-adjoint operators can be made"

No, it isn't. (See Barnett and Kraemer Phys. Lett. A 2002)

No-Signaling is Very General

Let \(\mathcal{A},\mathcal{B}\) be subalgebras of \(\mathcal{M}\) with \([\mathcal{A},\mathcal{B}]=0\). If \(E_i\in\mathcal{A}\) satisfy \(\sum E_i = I\), and,

\[T(A) := \sum_{i=1}^n E_i^{1/2}AE_i^{1/2},\]

then for all states \(\omega:\mathcal{M}\rightarrow\mathbb{C}\) and all \(B\in\mathcal{B}\),

\[ (T^*\omega)(B) = \omega(T(B)) = \omega(B). \]

Summary: For commuting systems, 'measuring' one doesn't affect the other

Continuous Symmetry
(\(U_t\) a strongly continuous 1-parameter unitary rep)

\[ \Updownarrow \]

Self-Adjoint Generator
(\(U_t = e^{itH}\) with \(H\) self-adjoint and conserved)

Does this mean observables are self-adjoint, since only the generator of a symmetry is an observable?

No.

1. Anti-Hermitian generator \(iH\) for \(U_t = e^{itH}\),
strictly speaking.

2. Non-self-adjoint operators are conserved too, including \(iH, e^{iH}, f(H), \dots\)