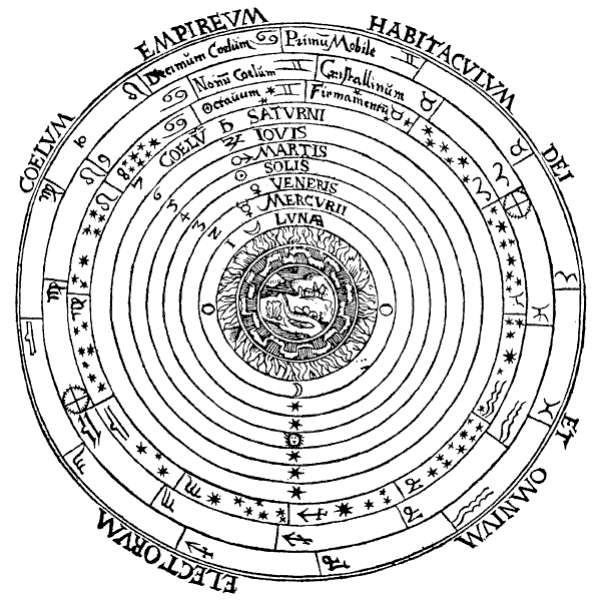
The fall the celestial spheres

In the last 400 years, we humans have largely lost our special place in the universe. The Greek-Roman astronomer Ptolemy (100-170 AD) described an Earth-centred model of the universe (below, left), surrounded by concentric 'celestial spheres' containing planets and the fixed stars, which was the standard model for over a thousand years. Copernicus (1473-1543) argued that in fact, Earth is just another planet orbiting the sun, and that it is the sun that is at the centre of the universe (below, right). In both cases, the objects visible to us in the sky all lie on celestial spheres. There was little role for 'empty space' in either description of the universe.

The 'celestial sphere' cosmologies of Ptolemy (left) and Copernicus (right).

Space came to play a more prominent role when Newton (1642-1726) proposed his law of gravity. Newton treated all gravitating bodies equally: all stars, planets, and massive objects follow exactly the same laws. On this picture, Earth his hardly special. We are just a little blue orb, orbiting a burning ball of hydrogen, floating around the vast emptiness of space, just like all the other stars and planets.

Space, littered with a few thousand stars and galaxies

Once you begin to think of our universe in this way, it is very natural to wonder, what is all that space? Is it a substantial thing, like water or air? Or, is it just a tool we use to talk about the locations of things?

These questions, and some of the deepest attempts to answer them, were formulated in an incredible battle of wits that took place between Gottfried Leibniz, one of the great scientists and philosophers of the 18th century, and Samuel Clarke, a philosopher writing on behalf of Isaac Newton. This debate is known as the Leibniz-Clarke correspondence.

How the battle of wits began

Leibniz's role in the debate is in part a response to Newton's Principia, the 1687 masterpiece of physics and philosophy also known by its full name, the Mathematical Principles of Natural Philosophy. This is the work where Newton set out his three laws of physics, as well as his famous law of gravitation. He published a revised addition in 1713, which Leibniz read. So, to set the stage, let's turn to an important discussion that occurs in Newton's work.

Substantivalism vs Relationism

In the 1713 revised edition of the Principia, Newton added a Scholium to his Definitions chapter. That Scholium formulated a perspective on space now known as substantivalism.

Substantivalism About Space. Points in space exist absolutely and independently of the matter contained in it.

Newton thought points in space were not only real but endowed with rich structure, which for example would allow one to say in absolute terms whether or not a body is in motion through space, a concept known as absolute motion. The alternative view, advocated by Leibniz, is called relationism.

Relationism About Space. Space is merely the description of particular relations between material bodies, such as the order in which bodies are arranged, and which does not depend on any substratum of spatial points.

The relationist denies the existence of absolute space, and therefore denies the possibility of absolute motion. So, how do relationists talk about motion? Most do so by developing a relational theory of motion, where everything that moves does so with respect to something else. We might say that a spaceship moves relative a planet; however, a spaceship passenger can equally say that the planet moves relative to the the spaceship. According to the relationist, motion of one thing relative to another is the only kind of motion that there is.

Relative motion: The ship moves relative to the planet; and equally, the planet moves relative to the ship.

In short, substantivalism is a realist view of space, while relationism is an antirealist view. The debate between these two perspectives is one of the most significant disagreements in the Leibniz-Clarke correspondence, and it is the one that we will focus on today.

To begin to think about what this distinction implies, imagine someone managed to destroy all the matter in the universe, so that there are no material objects at all. What would be left?

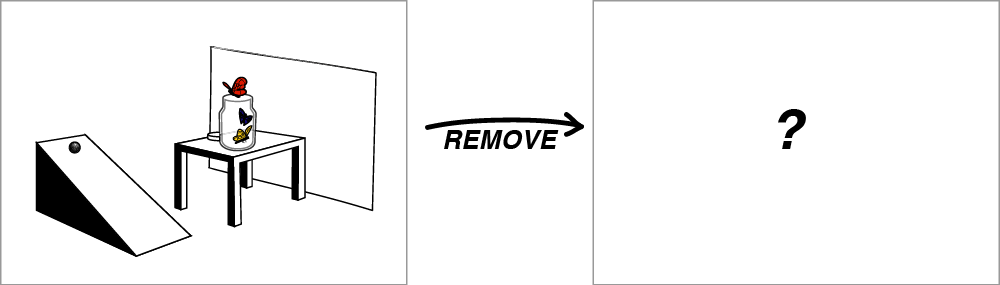
Substantivalism vs Relationism: What is left when you remove all matter?

The relationist would say, "Nothing". This is what Leibniz means when he says, "I maintain that there is no vacuum at all" (Leibniz, pg.8). By destroying all the matter, you have destroyed everything that there is! So, it is not possible for there to be a "vacuum" corresponding to empty space. In contrast, the substantivalist would respond, "Space" is what's left. Space is an immutable container, like a giant invisible Christmas Pudding, with matter placed in space like bits of fruit in the pudding.

Christmas pudding with fruit in it: A substantivalist model of space with matter in it

Newton's Bucket: The Reality of Space

Why did Newton support substantivalism? He gave a number of arguments. However, among the most famous, found in the Scholium to his Definitions in the Principia, is now known as Newton's bucket experiment. It reads as follows.

If a bucket is hanging from a very long cord and is continually turned around until the cord becomes twisted tight, and if the bucket is thereupon filled with water and is at rest along with the water and then, by some sudden force, is made to turn around in the opposite direction and, as the cord unwinds, perseveres for a while in this motion; then the surface of the water will at first be level, just as it was before the vessel began to move. But after the vessel, by the force gradually impressed upon the water, has caused the water also to begin revolving perceptibly, the water will gradually recede from the middle and rise up the sides of the vessel, assuming a concave shape (as experience has shown me)... . The rise of the water reveals its endeavour to recede from the axis of motion, and from such an endeavour one can find out and measure the true and absolute circular motion of the water (pgs. 58-59).

To understand Newton's argument, it's helpful to first imagine his experiment with no water in the buckets. One bucket rotates, and the other does not.

A non-rotating and a rotating bucket.

The substantivalist and relationist disagree about how to describe this situation. A substantivalist might say the left bucket is motionless with respect to absolute space, while the right one rotates absolutely. However, a relationist would say that there is only relative motion, and no absolute space; for example, a person rotating with the right bucket (imagine a tiny person standing on the edge) would say that this bucket is motionless, and that it is the left bucket that undergoes a complicated motion. So, who is right?

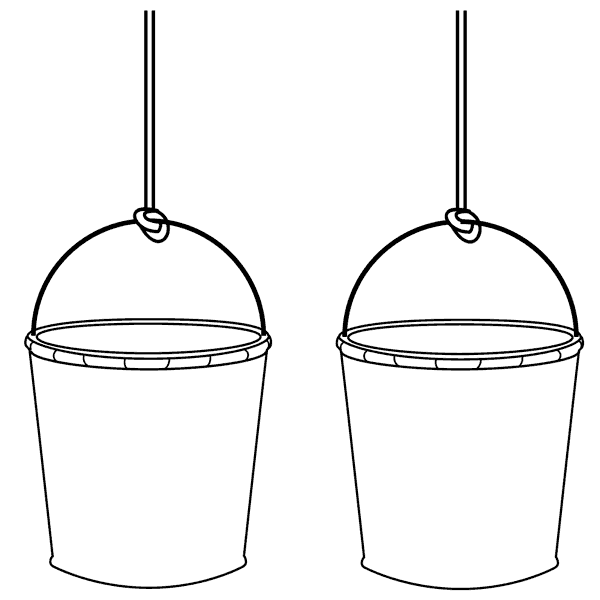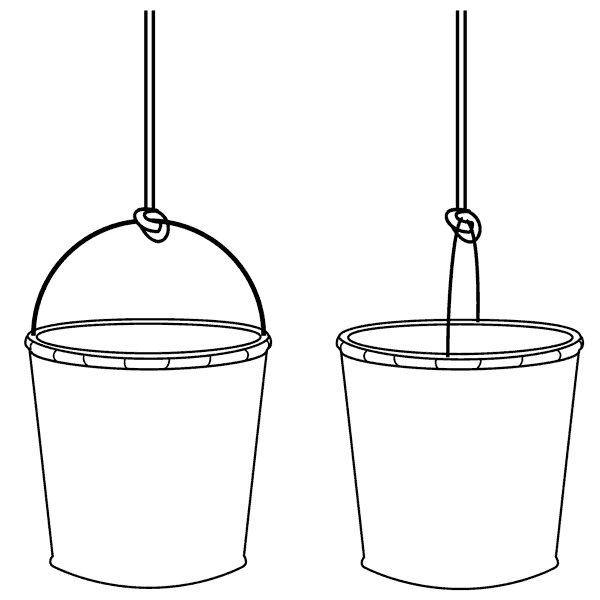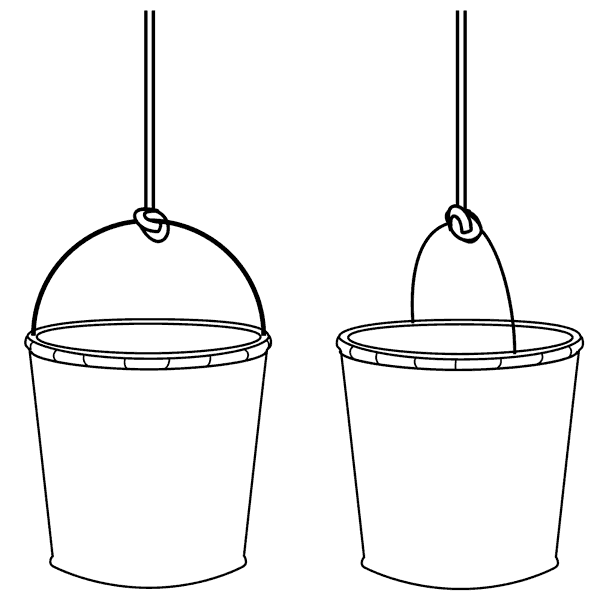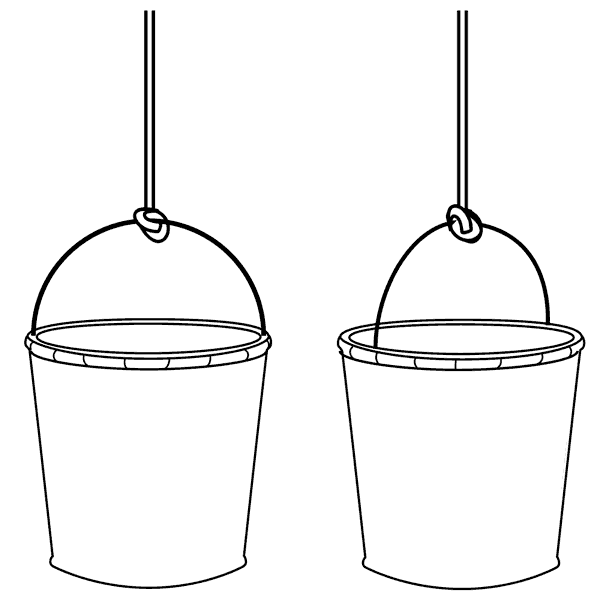
To try to settle this question, Newton imagines that the rotating and non-rotating buckets are each filled with water, as illustrated below.

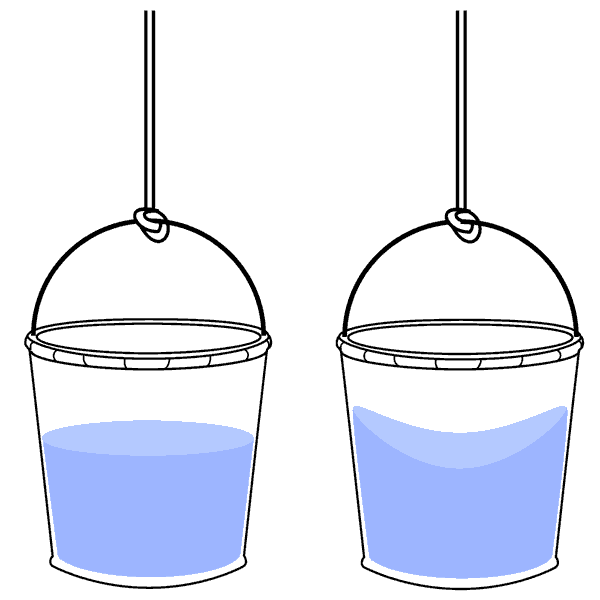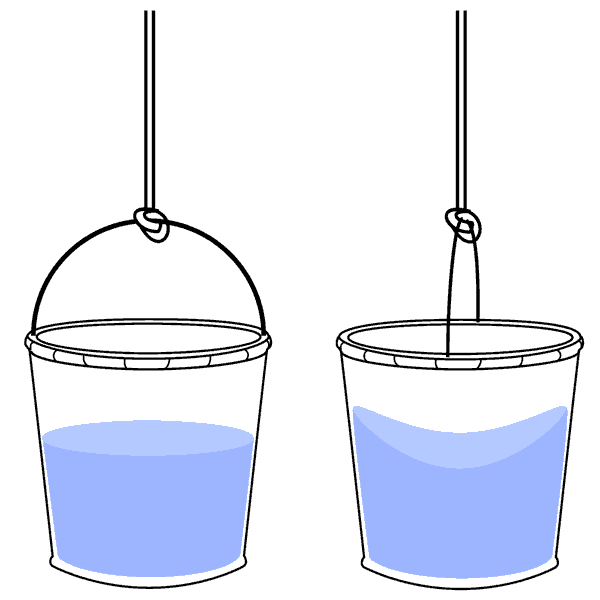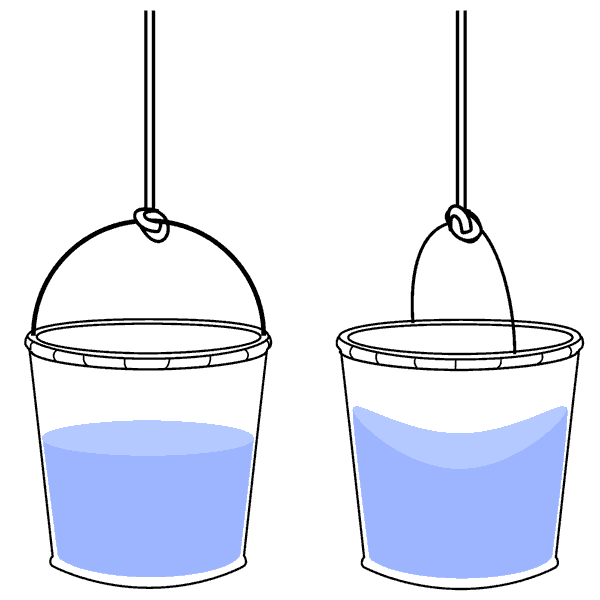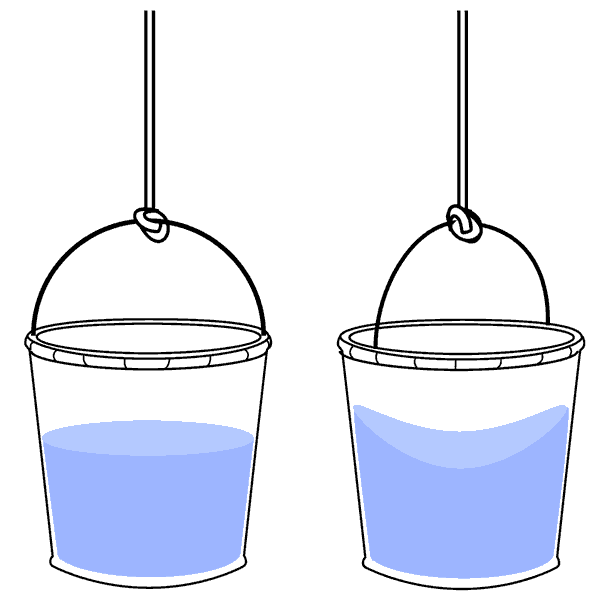
Newton's bucket experiment (Principia, Scholium to the Definitions)

Newton points out that all observers, including a rotating one, will agree that the water in the right bucket takes a concave shape. This, he says, is because the right bucket is absolutely in motion, in that it moves with respect to absolute space. Therefore, absolute space exists.

This is the backdrop for the debate between Leibniz and Clarke. Newton took himself to have established that space is absolute. Leibniz, in contrast, argued that this view is necessarily false.

Leibniz and Caroline vs Newton and Clarke

Leibniz disagreed with Newton's conclusion about space, and with much of Newton's philosophy and science. For the last two decades of his life, he was also embroiled in a priority dispute with Newton about the invention of the calculus. But in his later years, Leibniz settled down as official historian of the House of Hanover, and became the teacher and friend of Caroline of Ansbach, then Princess of Wales.

When Caroline's husband George ascended to the throne of England in 1727, she became Queen Caroline. The entire house moved to England. Although he stayed behind in Hanover, Leibniz felt compelled to warn his pupil Caroline about the dangers of Newtonian thinking. So, he wrote a letter to her in November of 1715. Caroline was impressed by the letter, and shared it with Samuel Clarke, who was Newton's parish priest. Clarke had also had mastered Newton's philosophy and physics, and was in regular contact with Newton (then Lucasian Professor of Mathematics at Trinity College, Cambridge). Clarke would have almost certainly discussed Leibniz's critical letter with Newton.

The result was a profound debate, carried out in a total of 5 letters from Leibniz and 5 responses from Clarke. Clarke's responses were very likely written in close discussion with Newton. The debate was only cut short by Leibniz's death in bed a year later, in November of 1716.

Round 1: The Watchmaker

The Leibniz-Clarke correspondence begins with Leibniz's November 1715 letter to Queen Caroline. The correspondence contains a number of powerful ideas and arguments about physics, philosophy and theology, on topics from the nature of physical laws, to the possibility of miracles, to the nature of space. It is worth reading all of it carefully. However, in this discussion, let us focus on the nature of space.

Leibniz's 1st Letter

Leibniz's initial letter makes four (numbered) remarks. The first is a complaint about the decay of England; the second is a complaint about Locke's materialism about the mind. However, his third and fourth are significant comments on the nature of laws and of space.

The concern in Leibniz's comments 3 and 4 centre on the analogy of a watchmaker. Leibniz imagines that the workings of the universe have been set up like an incredibly intricate clock. The basic analogy is:

Leibniz argues that the universe is like a perfectly made watch, set up in a way that is guided by laws of nature. These laws determine the workings of the universe, with no need for intervention: once one has established the laws and the current state of the universe, then like a clock, the system will evolve on its own without need for intervention. Thus, Leibniz writes:

"According to my opinion, the same force and vigor always remains in the world and only passes from one part of matter to another in agreement with the laws of nature and the beautiful pre-established order." (Leibniz, pg.4)

The role of God in the universe, for Leibniz, is that God created the 'clock', meaning that He initially designed the universe in the way he wanted it to run.

In the letter, Leibniz warns Caroline that according to Newton's view, the universe requires constant intervention in order to keep things moving the way they do. Such interventions are ready to occur at every location in absolute space, whether or not there happens to be anything there. Leibniz takes such an intervention to be a kind of 'miracle', and caricatures the doctrine as requiring that "God Almighty needs to wind up his watch from time to time" (Leibniz, pg.4).

Leibniz on Newton: "God Almighty needs to wind up his watch"

At this stage, Leibniz's argument against Newton is essentially theological: he finds Newton at odds with the requirement that God is a perfect, all-knowing creator. If God is perfect and knows what will happen next, then why would He create a flawed watch that must be regularly maintained?

However, this set the stage for an important response from Clarke about the nature of space according to Newton, and which led Leibniz to formulate an important objection against him.

Clarke's 1st Response

Clarke's response to Leibniz's theological argument is to reject the analogy. The role of the watchmaker is just to create the watch, whose design and movements are then "altogether independent of the artificer" (Clarke, p.6). In contrast, Clarke argues that the workings of the universe depend on God for their very existence.

However, he then makes a comment that substantially clarifies the Newtonian picture of the role of space. According to Newton, a force (such as gravity) exists everywhere in space. You may know that, according to Newton's 2nd law, a net force F gives rise to a tendency to accelerate, via Newton's second law F=ma, where a is the acceleration and m is the mass. For example, if we place a particle anywhere in space near the Earth, then it will be attracted by the force of the Earth's gravity.

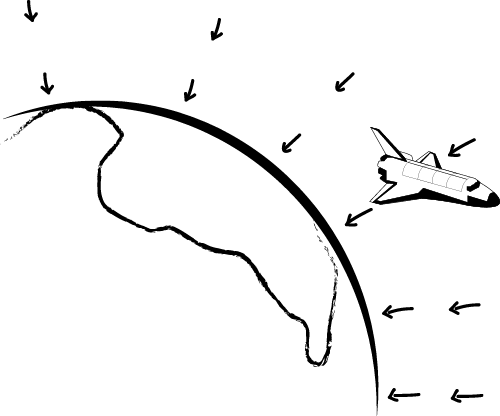
Newtonian Gravity: a force occurs everywhere in space, drawing objects towards Earth.

So, for Newton, absolute space plays an essential role in our description of the furniture that makes up the physical world: it is the arena throughout which forces exist.

With this picture in the background, Clarke identifies what he takes to be the essential role for God in this description. A force spread throughout space provides a constant source of power, which will move any object that is set in that space. Clarke says that there is a kind of 'source' for this motive power, namely, God: He is the "continual preserver" of forces in space (Clarke, pg.6). You might think of this as the view that forces are like light bulbs: Clarke suggests a force needs a constant source of power in order to work, just as a light bulb does. But whereas a light bulb is powered by electricity, forces more generally are "powered" by God.

For Clarke, forces are light light bulbs, but which are continuously powered by God

This view has a natural theological consequence as well. Clarke concludes that in order for this theory to work, God must be omnipresent: He exists at every point in absolute space. In particular, God plays a constant and essential role in the workings of the universe through the maintenance of forces.

In contrast, Clarke accuses Leibniz of providing a less distinguished role for God, according to which God is only really needed for one activity at the outset, in order to set the pre-established harmony. Clarke finds this disagreeable, writing:

"If a king had a kingdom in which all things would continually go on without his government or interposition, or without his attending to and ordering what is done in the kingdom, it would be to him merely a nominal kingdom, nor would he in reality deserve at all the title of king or governor" (Clarke, p.6).

Round 2: Metaphysical principles and miracles

Leibniz's second letter was sent about a month after the first, at the end of December, 1715. This letter begins by setting out a disagreement about the very approach of Newton's Principia. The book is largely modeled after Euclidean geometry. Like Euclid's Elements, Newton begins with a short list of definitions, followed by a few axioms (now known as 'Newton's laws'), followed by derivations of consequences of the axioms. The title of the book reflects this approach: "Mathematical Principles of Natural Philosophy."

In contrast, Leibniz says that would should actually do is begin with metaphysical principles. There is of course room for disagreement as to whether or not Newton's laws are metaphysical principles as well. However, one can also read the objection as asking us to adopt Leibniz's principles instead of Newton's. For example, Leibniz takes it to be a basic fact of metaphysics that "a proposition cannot be true and false at the same time" (Leibniz, p.7); this is known as the 'principle of contradiction'. For the purposes of his discussion with Clarke, the more interesting metaphysical principle that Leibniz advocates is one that you are already familiar with, the 'principle of sufficient reason':

Leibniz's Principle of Sufficient Reason: "Nothing takes place without a sufficient reason; in other words, that nothing occurs for which it would be impossible for someone who has enough knowledge of things to give a reason adequate to determine why the thing is as it is and not otherwise." (Leibniz 1714)

Another metaphysical principle that is central to Leibniz's thinking about space, which appears in his fourth letter to Clarke, is something that you are familiar with as well. It is a special case of 'Leibniz's Law':

Leibniz's Principle of Identity of Indiscernibles. Entities have exactly the same properties only if they are in fact one and the same entity.

Leibniz says the Principle of Sufficient Reason can be used to derive a great deal of the physical predictions that Newton purports to derive from Newton's laws. So, although Leibniz agrees with many of Newton's predictions, he takes Newton's derivations to establish them incorrectly.

As for Clarke's account of the Newtonian role for God in space, that God intervenes on the natural world through the maintenance of forces, Leibniz finds this objectionable too. According to Leibniz, God only intervenes in a way that endows something with "goodness"; so, God provides all that is good in the world. But God does not intervene on the natural world, since that would amount to an implausible 'miracle'.

Leibniz's argument for this last point takes the form of a dilemma: if God were to intervene on the natural world through miracles, then that intervention must either be "supernatural" or "natural", the latter meaning in accordance with the laws of nature. According to Leibniz, supernatural intervention would be the kind of miracle that could be used to explain anything at all, and which would therefore explain nothing. On the other hand, "natural intervention" would be unsuitable for a deity and supreme intelligence. Since neither option is desirable, it must be that God doesn't perform miracles at all.

Clarke responds by denying the distinction between natural and supernatural, arguing that the actions of God might be described by us in either way. This leads Leibniz to formulate a much more powerful argument, which appears in the third round of letters.

Round 3: The 'Shift' Argument from Sufficient Reasons

In his third letter, Leibniz formulates one of the most important philosophical objections to substantivalism, known as the shift argument. This argument remains an important part of the discussion of space and time, even from the perspective of modern physics; it even turned out to play a crucial role in the development of Einstein's theory of space, time and gravity, general relativity (through an argument now known as the 'hole argument'). Leibniz's objection goes as follows.

Leibniz begins by reiterating his relationist perspective on space: "I hold space to be purely relative.... I hold it to be an order of coexistences, as time is an order of successions" (Leibniz, pg.14). In particular space is a statement of relational property, such as an ordering of a collection of objects, and so it is a relationist perspective on space.

He then proceeds to give the famous shift against substantivalism about space. It can be reconstructed as follows.

You should check that this is a valid argument of the form: A implies B; B implies C; Not C, Therefore, not A. But is it sound? That is, are the premises true?

Leibniz's concern is simple and deep: if space exists independently of the matter it contains, then there would be a difference if we shift all matter in the universe by two meters in some direction. But what reason could we possibly give for saying that matter is arranged in one of these two ways? This would seem to be a serious explanatory shortcoming in the substantivalist perspective on space.

A 'Leibniz shift': moving all matter in the universe 2 meters to the right.

Moreover, the relationist has no such problem. Since space has no independent existence, Leibniz would say that the two descriptions are in fact one and the same: since all the relations between objects are the same, the shift transformation actually leaves the description of the universe completely unchanged.

Clarke, in his third reply, accepts that the Principle of Sufficient Reason is true. However, he does reject Leibniz's conclusion, and does so by denying premise 2. Clarke appeals in particular to theology, asserting that God's will is a sufficient reason to explain why matter is arranged the way it is.

But Leibniz anticipated this move at the end of his third letter, arguing that the shift argument is a problem even from the perspective of theology. For it would seem to imply that God acts for no reason. But this would seem to be a major shortcoming in God's perfection, which Leibniz takes to be unacceptable.

Thus, Clarke attempts a second response: perhaps the reason is that if one describes a matter distribution and then shifts it, then the "spaces are really different or distinct one from another, though they are perfectly alike". If this is the case, then there might be a reason to prefer the actual location of things as opposed to the shifted location, either due to God or something else, in a way that satisfies Leibniz's Principle of Sufficient Reason.

This leads Leibniz to give a predictable response.

Round 4: The Identity of Indiscernibles

Clarke's last move suggested that even though space is perfectly homogeneous, that there is still a difference between the shifted and the unshifted description.

Leibniz response is that this would violate the Principle of Identity of Indiscernibles. Namely, two descriptions related by a shift in homogeneous space are completely indiscernible from one another. As a consequence, Leibniz infers, they must be identical — they are one and the same space after all.

Indeed, one can formulate the entire shift argument on the basis of the Principle of Identity of Indiscernibles as well. Namely, if space were absolute and homogeneous, then a Leibniz 'shift' would produce a state of affairs that is not identical but indiscernible from the original; but nothing is ever indiscernible and not identical; therefore, space is not absolute and homogeneous.

Clarke's main reply to this, in his final letter to Leibniz, is to deny the principle of identity of indiscernible. Whether or not this is a reasonable response, I leave up to you.