A. Questions for Submission

2.1 Time dilation and length contraction

Review the derivation of time dilation and length contraction from the course videos and readings, and then consider the following.

A muon is a particle created when cosmic rays strike the Earth's atmosphere. It descends from the atmosphere down to our detectors on the ground with incredible speed, roughly 90% the speed of light. However, the typical lifetime of a muon is 2 microseconds from the perspective of an Earth observer, which is not enough time for it to reach the ground. How is it possible for such muons to be registered by our detectors? Explain your answer:

1. ...from the perspective of an Earth observer who witnesses the fast-moving muon (hint: use time dilation)
2. ...from the perspective of a hypothetical observer who is `riding along' in the same reference frame as the muon (hint: use length contraction)

2.2 Synchronisation

Identify two situations in ordinary life in which the concept of `synchronisation in different spatial locations' matters, such as in the performance of a group of musicians. In what way is this synchronisation disrupted by an observer moving in a different reference frame? Why didn't anyone notice this before Einstein?

2.3 Relativity of simultaneity

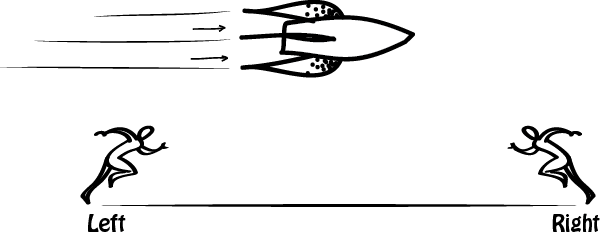
Suppose you stand next to a racetrack. Two runners begin on opposite sides of the track and race to reach the centre of the track. From your best measurements you judge the race to be fair, because the left-runner and the right-runner start running at the same time. Now imagine that an observer on a spaceship then whizzes by from left to right at very high speed and observes the same scenario. It will look to the spaceship observer as if the track is whizzing by from right to left.

↓ Earth Frame of Reference ↓

↓ Spaceship Frame of Reference ↓

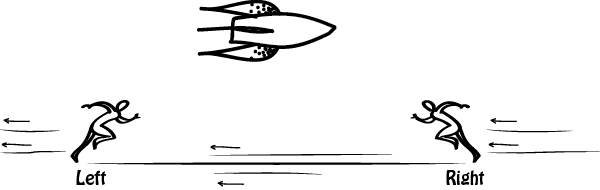
Which of the following will be judged to be true by the spaceship observer?

1. the right (trailing) runner to begin first
2. the left (leading) runner to begin first
3. the two runners to begin at the same time

 

B. Further Discussion (No Submission)

1) Suppose you are on a spaceship travelling away from the Earth at a constant speed of 90 percent the speed of light and in a straight line. There is a ruler at rest on the spaceship, which before takeoff was measured by a spaceship observer to be 30cm long. How long will the spaceship observer measure the ruler to be once the spaceship is in motion?

2) Consider the following example.

• Two identical spaceships pass one another, moving rapidly in opposite directions at the same speed according to an observer on a nearby planet. The planet observer judges that both spaceships have shrunk the same amount due to relativistic length contraction. So they are the same length and, in conformity with this expectation, the planet observer notes that the two spaceships line up perfectly as they pass.
  
  An observer on one of the spaceships, however, finds the other spaceship to be moving rapidly. So that spaceship observer judges the other spaceship to have shrunk relative to the first spaceship. And an observer on the second spaceship comes to the reverse judgment, that the first spaceship has shrunk.
  
  How is it possible for all of of them to come to such different judgements?

Two observers I and II both stand on a large platform. There are two lightning strikes, A and B.

The locations and observations of the observers are the following.

• Observer I is located at the midpoint of the spatial locations of the strikes A and B. Light signals coming from the strikes A and B arrive at this observer I at the same time.
• The observer II is located much closer to the strike A. As a result, the light signal from strike A arrives at observer II much earlier than the light signal from strike B.

Thus, Observer I sees the signals at the same time; observer II sees them at different times. Is this difference the relativity of simultaneity of relativity theory? If not, why not?