Introduction

This note is about what's so strange about entanglement, in brief and non-technical terms. We begin with a review of the nature of position and momentum. We'll then see the basic idea of entanglement as described by Einstein, Podolsky and Rosen (EPR) in their famous 1935 paper, and finally discuss why it's peculiar.

Incompatible quantities

A quantum state with definite position can be viewed as an amplitude occurring in a narrow region of space:

De Broglie's matter-wave law says that momentum = h × wavelength, where h is Planck's constant. So, a quantum state with definite momentum is a wave with definite wavelength:

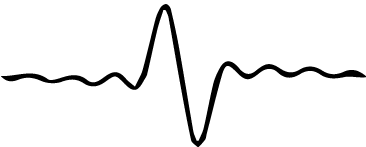
The definite momentum state above is visibly a superposition of definite position states.

So, if we begin with a quantum state that has definite momentum, and then measure the position, our position measurement is indeterministic. Sometimes we will measure one position, and sometimes we will measure another, according to some probability. This is an expression of Heisenberg's uncertainty principle. It also makes sense given how De Broglie defines the momentum of a quantum state.

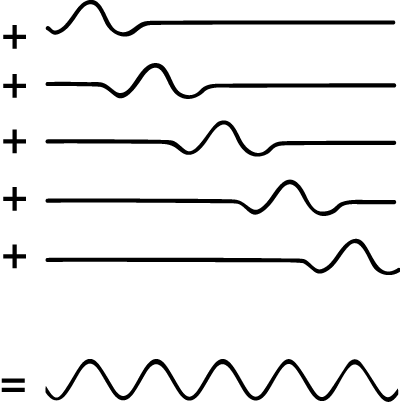
The situation is symmetric for position: it turns out that a definite position state is also superposition of definite momentum states.

This means that if we begin with a quantum state with definite position, and then measure the momentum, our momentum measurement is indeterministic. Sometimes we will get one one momentum, and sometimes we will get another, according to some probability. This is the other side of Heisenberg's uncertainty principle.

Quantities that cannot be jointly observed are called incompatible. Position and momentum are one example. As we will see, this incompatibility is an essential part of identifying the strangeness of quantum entanglement.

Entangled Particles

Entanglement is a special kind of quantum state that can occur for a pair of quantum particles. Suppose we have two particles, and that we trap each particle in a different box. Each box has two sides, Left and Right, with a divider in the middle.

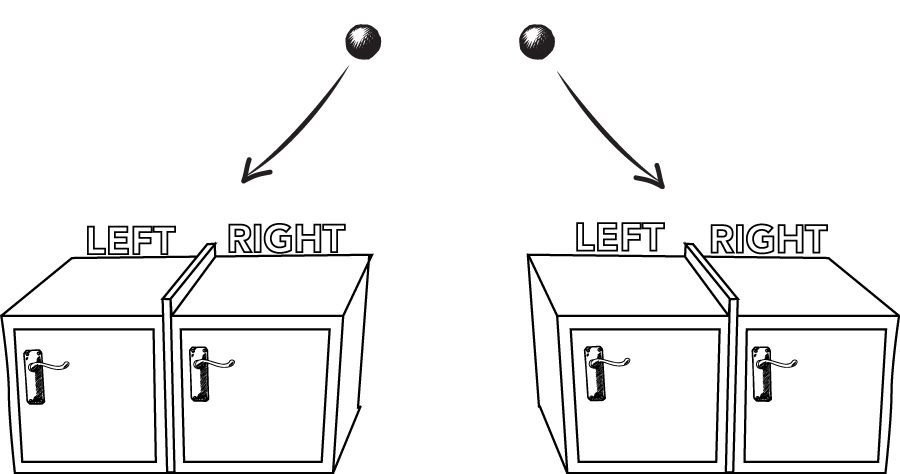
Suppose also that the particles are placed so that each particle is equally likely to be in either side of its box, and the particles are guaranteed to be in opposite sides. This is possible, for example, if an atom decays in such a way that emits two particles in opposite directions at one of the two angles indicated below.

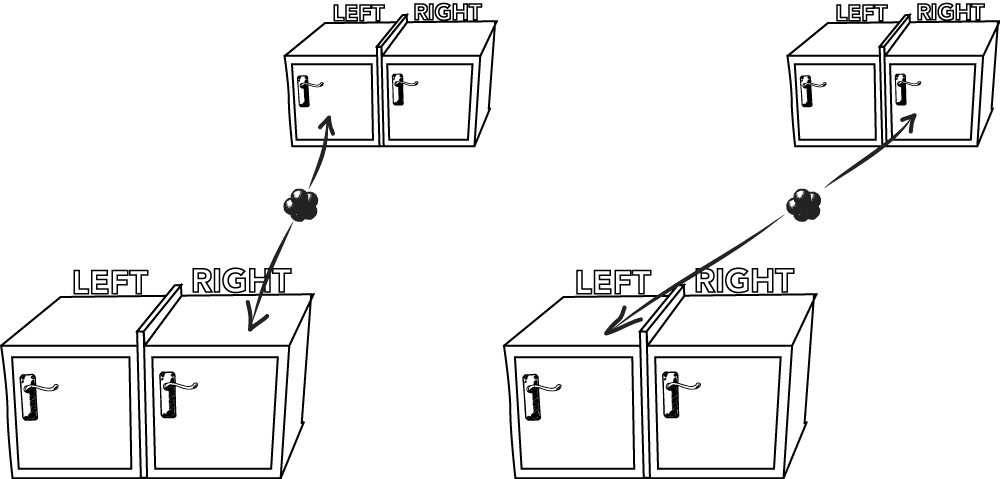
Suppose we now separate the two boxes by keeping one on Earth and sending the other to the Andromeda Galaxy 2.5 million light years away. The particles have been prepared in a superposition: Earth-Left and Andromeda-Right, or Earth-Right and Andromeda-Left. What will happen when a measurement will be made on Earth?

If an Andromeda scientist were to open the Andromeda box, it would immediately determine the description of our Earth box. If the Andromeda particle is on the Left, then the Earth particle is immediately known to be on the Right, and vice versa. The result takes place in the course of a moment, much faster than the time required for light to travel, with measurements in an arbitrarily distant location apparently having an immediate affect on experiment.

Many discussions of entanglement stop here. But this would be missing the full strangeness of quantum entanglement. To illustrate that we have not yet arrived at anything particularly strange, here is an example using an ordinary rock in classical mechanics.

An Ordinary Rock

Consider an ordinary rock sitting on top of a bomb. Let's describe rock using entirely non-quantum ideas, such as the idea that the total momentum of the rock is conserved. This means that if the bomb blows the rock into two pieces, then they must fly in exactly opposite directions, since their momenta must sum to zero.

We can describe a scenario very similar to the one above: suppose that a rock explodes in such a way that two pieces each fly into a divided box. Each piece of rock is equally likely to be on either the left or right side, and guaranteed to be on the opposite side of the other piece.

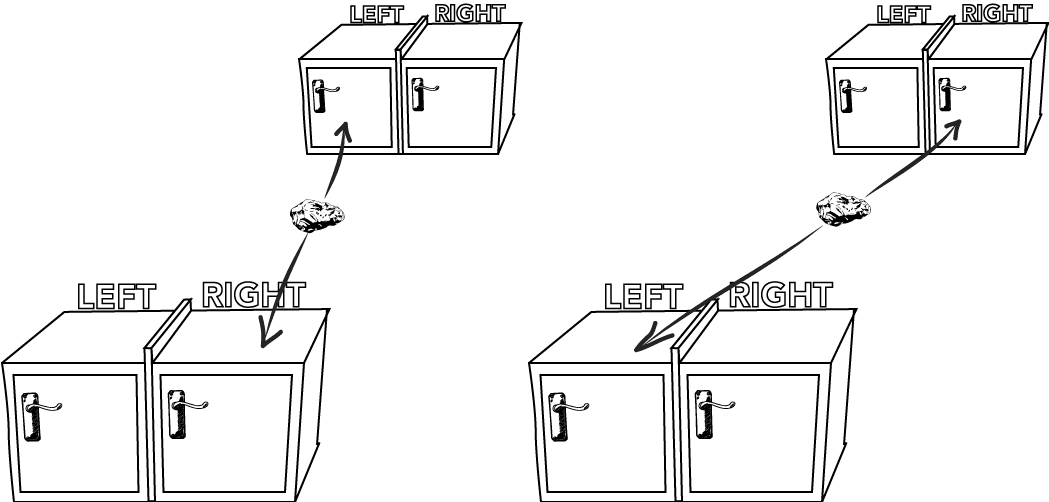
As in the previous case, one of these boxes can now be sent to the distant Andromeda galaxy. When a distant Andromeda scientist opens the box, they immediately determine a fact about our box on Earth. And yet, there is nothing strange about this. No signal was transmitted, no superluminal effect occurred — nothing about the arbitrarily distant rock caused anything to happen to the Earth rock. The two boxes are simply anti-correlated because of how they were prepared.

So, this much of our description of quantum entanglement in the first example can be described using a perfectly ordinary rock. However, the situation with quantum entanglement also turns out to be much worse than this in a subtle way.

What's Really Strange

Here is why quantum entanglement is not like the exploding rock. Suppose someone living in the Andromeda galaxy chooses to measure the position of the particle in the Andromeda box, determining (say) that it is on the left side. Then the outcome of the Earth box is completely determined: it must be on the opposite side.

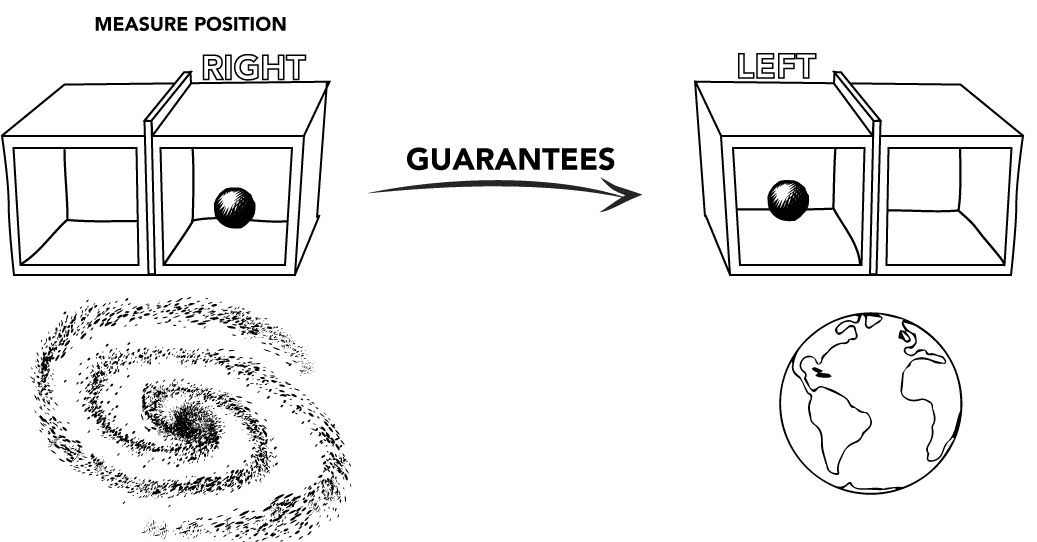
On the other hand, suppose the Andromeda scientist chooses to measure the momentum. Then the Andromeda particle is in a superposition of definite position states. Since the Earth particle must be anti-correlated, this means that the Earth particle is also in a superposition of definite position states.

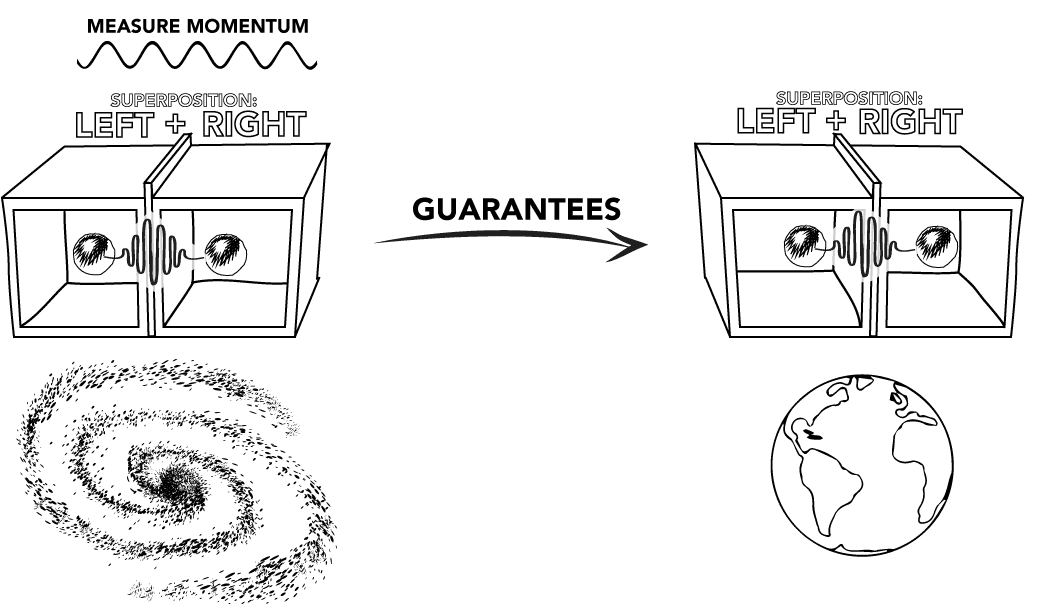
What's strange is that the state of the Earth rock in some sense depends on the choice of the distant measurement. If the Andromeda scientist chooses to measure position, then the state of the Earth rock is immediately determined. But if it chooses to measure momentum, then the state of the Earth rock is immediately reduced to a superposition of position states, which will sometimes lead to a Left-side measurement and sometimes a Right-side measurement. Which one is the case depends only on the choice of measurement on Andromeda. And it has an immediate effect on Earth measurements, in spite of being an extreme distance away.

In fact, the Andromeda galaxy is so distant that even a light signal (which travels at the "maximum speed" known to be possible in the vacuum) could not communicate the effect in time. So, if it is some sort of physical "collapse" that gives rise to the change in the entangled system's state, then that effect would appear to propagate faster than the speed of light.

Compare this situation to the ordinary rock, described using non-quantum ideas. With the rock, the Andromeda scientist could choose to measure the momentum of the rock in the Andromeda box, or its position. This choice makes absolutely no difference to the rock in the Earth box. The position of the Earth piece is determined in both cases, and in particular anti-correlated with the position of the Andromeda piece. No faster-than-light propagation occurs here.

No Signalling

It is widely believe that faster-than-light travel is impossible. We have never detected any particle travelling faster than light. We also know from Einstein's theory of special relativity that if a particle begins at a speed that is slower than light, then it cannot be accelerated to go faster than light unless an infinite amount of energy is used. Does this mean that we should be worried about entanglement?

Possibly. It depends on how one interprets what quantum mechanics says about the world. As we saw last time, there are a number of different possibilities, from many worlds to a physical `collapse' phenomenon.

However, even if entanglement does lead to a faster-than-light occurrence, it turns out to be censored from view, in that it is not possible to use this effect to send a faster-than-light signal to a distant location in the universe. This constraint is sometimes referred to as no-signalling.

Suppose we try to use entanglement to send a signal. A friend of ours agrees to go to a distant planet and search for life. Before she leaves, we prepare not just one pair of entangled particles, but a large ensemble of entangled particles, and send one from each pair with her on her journey. We agree that if she detects life, then she measure the position of all the particles; otherwise she will measure the momentum of all of them. Will she be able to use this strategy to communicate to us instantaneously?

The answer is no. If she detects life, and thus measures position, then the position states of the Earth boxes will all be determined. If she instead detects no life, and thus measures momentum, then the position states will be in a superposition of Left and Right. But in both cases, when we open the Earth boxes, we will simply find that the particles are half on the left and half on the right. We don't know which specific value our friend's measurements produced, only that she made a measurement. So, our detection is the same in both case.

This turns out to hold quite generally in quantum theory: it is impossible to use entangled particles to send an instantaneous signal. So, curiously, whether or not entanglement gives rise to a faster-than-light process appears to be completely unobservable to us.

Non-Separability and Non-Locality: A Disturbance in the Universe

Although no-signaling may provide us with some reassurance about the nature of entanglement, there remains a deep problem for the very nature of experiment.

Much of science depends on our ability to isolate a system from its environment, at least approximately. For example, when we see a leaf on a tree fluttering in the wind, it might confuse us to search for a mechanism in the workings of the leaf that explains its fluttering motion. We use avoid such problems by placing the leaf in an isolated environment, without wind, in which we can study the structure of the leaf without worrying that its behaviour is being artificially altered. So, although a leaf is often an "open system" in the sense that it is not isolated from its environment, it is easy enough for us to isolate it for the purposes of study.

In quantum mechanics, there is a strong sense in which entangled particles are not isolated from their environment. If a particle on Earth is entangled with on in the Andromeda galaxy 2.5 million light years away, then disturbances in that galaxy may have a regular (and possibly dramatic) effect their corresponding particles on Earth.

Albert Einstein

Einstein was seriously concerned about this problem, as reported by Don Howard:

"However, if one renounces the assumption that what is present in different parts of space has independent, real existence, then I do not at all see what physics is supposed to describe. For what is thought to be a 'system' is, after all, just conventional, and I do not see how one is supposed to divide up the world objectively so that one can make statements about the parts."

Is it possible that particles in the Andromeda galaxy are entangled with particles on Earth? It certainly is. All the particles in the universe were once extraordinarily close together in the early moments after the big bang, at which point it is entirely possible that they became entangled. There are also a number of formal results in the mathematical foundations of quantum theory that show that entanglement with distant universes is both common and difficult to undo. This raises deep questions about how it is possible to carry out any experiments at all on Earth, which deeply worried Einstein himself:

"Without such an assumption of the mutually independent existence ... of spatially distant things, as assumption which originates in everyday thought, physical thought in the sense familiar to us would not be possible. Nor does one see how physical laws could be formulated and tested without such a clean separation."

— Einstein, as quoted in Howard (1985), "Einstein on Locality and Separability," pg.171-201.