The epistemology of science

The remarkable practice of thought experiments is one way to gain information about the empirical world. This is an example of the shockingly clever techniques available to science. Science is unquestionably the most reliable knowledge-gathering tool that we have.

The Hubble Ultra-Deep Field

But how exactly does science allow us to gather knowledge? One answer is that there seem to be methods and principles particular to science that make it so successful. Today, we begin the exploration of what those methods are and how they work.

The problem is much harder than it seems at first.

Confirmation by induction

The first and oldest attempt to describe scientific method is now referred to as induction. The basic idea is simple: science just generalises observations beyond what we have actually observed. As the name suggests, this is not the most sophisticated approach that one might take. Here's how it looks in action.

Suppose we want to check the florets at the center of a sunflower are arranged in golden spirals.

We can check this by observing that the arrangement of the florets in many different sunflowers, in many different locations and growing conditions, are all arranged in golden spirals, and conclude inductively that this is a general property of sunflowers. Further evidence can be gathered by observing many instances of plants growing in the most efficient pattern possible. The mathematician Helmut Vogel showed in 1979 that this sunflower pattern is an automatic consequence of adopting the most efficient floret packing algorithm.

The general form of this reasoning can be outlined as follows.

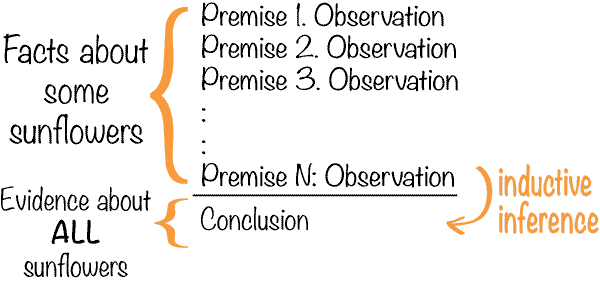
Because of this character, inductive arguments are sometimes called ampliative, in that the conclusion goes beyond the information contained in the premises. This is quite the opposite of what happens in a deductive inference, in which the conclusion can contain no more information than what was already contained in the premises.

When we formulate inductive reasoning as a precise rule of inference, it is called a principle of induction.

Naïve inductivism

One particularly simple principle of induction is called enumerative induction. This principle says that if we observe a large number of instances in which something has a property, then we can infer that property in general.

Enumerative induction enjoys some limited success. It allows me to successfully predict that it will rain in London in the month of April, and that the sun will rise tomorrow. It has happened many times before, and we can be confident that it will happen again.

... ...

However, enumerative induction does not work in general. For example, I may determine that I have been alive for 10,000 days so far, but this does not provide evidence for the claim that I will live forever. On the contrary, at some point at the end of this sequence I will almost certainly be observed dead.

... ...

Another example is the stock market. Prior to 2007, the housing market had risen during nearly every 1-year period since 1991. Some said it would rise forever. As you know, it did not.

A somewhat more interesting principle is what is known as Naïve Inductivism. This is the view that, if something is observed many times to have a property, and:

• These observations occurred in many different circumstances, and
• no counterexample has yet been found

then one may infer that it has the property in general. In other words, naïve inductivism is just enumerative induction with some caveats to make it a bit less susceptible to flaws.

But even with this modification, a further concern about the view is that it allows no room for scientific realism (realism is discussed in Chapter 8 and Chapter 9). Scientific Realists view the unobservables associated with our most successful scientific theories as being approximately true. But if naïve induction is the only way to acquire knowledge, then we cannot know unobservables like quarks and dark energy are even approximately correct, since they do not follow from the simple generalisation of direct observations.

So, naïve inductivism appears too weak to allow the kind of scientific inference that leads to realism.

HD Confirmation

In the 20th century, induction was quickly recognised to be too weak, and a more robust approach to scientific knowledge was proposed: the more general confirmation of theory by evidence. On the simplest such view, one acquires scientific knowledge by proposing a body of theory, deducing an empirical prediction, and then collecting empirical evidence that confirms the theory. This is known as the Hypothetico-Deductive theory of confirmation.

As an example, suppose you formulate the hypothesis that water boils at 100°C. Your hypothesis entails the testable prediction: if you put a pan of water on the hob until it starts boiling and then measure the temperature with a thermometer, the thermometer will read 100°C. So, you carry out the test.

Sure enough, when you measure the water temperature, it is indeed 100°C. So, you consider the hypothesis confirmed. Of course, further confirmation is still possible by reproducing the experiment under other circumstances. Indeed, in some situations, such as at a very high altitude, you will find that the hypothesis is falsified, and therefore have to introduce some further caveats and test your new hypothesis. But you get the idea. This simple picture is how most people, and indeed most scientists, tend to think of the scientific method before reflecting on it for very long.

The Paradox of the Raven

Unfortunately, the philosopher Carl Hempel pointed out that this simple expression of induction has a serious problem, now known as Hempel's Paradox of the Raven. This problem quite simply and utterly destroys the simple HD characterisation of the scientific method.

Suppose we are interested in testing the hypothesis, All ravens are black. This hypothesis logically entails the statement "If something is a raven, then it's black." So, we only need to go out and check some ravens to see if they agree with the statement that

By encountering a raven that is black, we confirm that the statement, "If something is a raven, then it's black" is true. According to the logical response, this provides evidence for the statement that "All ravens are black."

You may find this similar to what you might have called "The scientific method" in school. The trouble is, it doesn't work. By the same reasoning, we could use all kinds of crazy observations to provide evidence for our hypothesis, but which clearly have nothing to do with it.

Go back to our hypothesis that all ravens are black. It also logically entails the statement, "If something is not black, then it's a non-raven." There are many observations that we can use to confirm this statement. A white shoe, a banana, a football — all of these objects confirm that not-black things are non-ravens.

According to the logical response, these observations all provide evidence for the hypothesis that all ravens are black, for the same reason that a black raven does. But this is absurd! A white shoe has nothing to do with the hypothesis. Nor does a banana, nor a football. These observations do not confirm the hypothesis that all ravens are black. Something has gone horribly wrong.

The Duhem-Quine Problem

Our discussion of confirmation theory so far as been a little bit logical and abstract. Let's go back to thinking a bit more practically, as an experimentalist might do. Is it possible to confirm a theory by carrying out some sort of procedure in a lab? If so, then what exactly should that procedure be like? In particular, what would we have to do in order to be sure that we test the right thing?

For example, members of the Church of Scientology believe that a modified ohmmeter known as an E-Meter can make predictions about one's mental state. So, if I have a theory that your mental state will change by tomorrow, I could test and confirm this prediction by comparing readings of an E-Meter.

However, this "confirmation" only holds given the gigantic auxiliary assumption that the E-Meter can detect mental states. If the auxiliary assumptions fail then I will not have confirmed my theory. And indeed, since an ohmmeter detects the electric conductivity of the skin, the same reading might be produced if the heat of the day causes you to sweat more tomorrow.

This same problem can occur in any science or social science as well: auxiliary assumptions about how an experiment works can seemingly always confound our attempts to confirm our theories. This problem was originally suggested by the French philosopher of science Pierre Duhem in the context of physics, and given a slightly more general statement by Quine.

Duhem argued in particular that in physics, "without theory it is impossible to regulate a single instrument or interpret a single reading." Thus he concluded that we never really confirm anything at all.

This is not just a problem for philosophers of science, but a problem for scientists as well. Go back to the boiling water example, in which we confirmed that water boils at 100°C.

What did we assume to make this experiment work? There are many. For example, we assumed that:

• The minerals and other impurities in the liquid did not effect the reading.
• The thermometer accurately reflected the temperature of the water.
• The room was not at a high enough pressure to cause super-heating.
• The inside surface of the pot was normal, and not overly smooth, which can also cause super-heating.
• The temperature did not change between the moment that the water boiled and the moment that we inserted the thermometer.

Each of these assumptions themselves requires a great deal of background knowledge. And there are probably many other things that we assumed as well. That is, our "confirmation" of the boiling point required a considerable number of auxiliary assumptions in order to be correct.

That is the Duhem-Quine problem. It reflects in part the difficulty of isolating the hypothesis you wish to test. More deeply, it also represents an inherent difficulty with inductive confirmation. That said, the argument is only as powerful as its premises. Are either premise 1) or premise 2) something that you might challenge?

Hume's Problem

A further difficulty with inductive confirmation was first pointed out by David Hume.

Remember that inductive confirmation requires some sort of principle of induction, which allows us to begin with observations and infer to a more general conclusion. Hume begins by asking, what is the justification of any principle of induction? Why is this inference rule allowed? The problem is that there doesn't seem to be any good answer to this question.

We could just observe that induction has been justified many times in the past, and then infer that it must be justified in general. But then then what justifies that inference? If we say it is the same principle then our argument is circular. If we say it is a different one, then we appear to be stuck on an infinite regress, forever introducing more principles to justify the first one.

On the other hand, we could try to derive induction deductively. But it is hard to imagine how that could look beyond something like the following.

1. If a principle has been justified on many instances, then it is justified in general.
2. Induction has been justified on many instances.
3. Therefore, induction is justified in general.

This of course a valid deductive argument. But it isn't very convincing. For what reason do we have to believe the first premise?

So, there is a question as to what justifies induction. However, there is also a somewhat deflationary response to this worry, which is to refuse to answer the question.

This is the position advocated by Sankey, who argues that worries about Hume's problem are demanding an unreasonably high standard of justification for induction. He suggests instead that induction is already justified enough, and that "[n]o higher standards of justification exist over and above those employed in successful scientific practice or in common-sense interaction with the world."

This kind of account requires a little more filling out to be plausible. For example, Sankey does not provide a standard for determining which propositions need justification and which do not, which makes the proposal difficult to evaluate.

However, one option could be that induction is simply a mechanical part of human thought and language, just like many have argued that deductive logic is, and therefore requires no more justification than deductive logic does. Then our main problem is just to determine what is the correct logic of induction. We have so far not seen one that is completely plausible. We will introduce some slightly more plausible accounts that make use of probability theory next time.