The Problem of Underdetermination

The Problem of Underdetermination is an objection to the No Miracles Argument. Recall that the best explanation premise was an essential part of the No Miracles argument. Let's now think a little bit harder about this premise. Is truth (or approximate truth) really the best explanation of success?

The problem of underdetermination is that there can sometimes be multiple incompatible theories, which give equally good predictions and explanations, but none of which are "determined" or "chosen uniquely" by existing evidence.

When underdetermination occurs, one cannot consistently infer that the best explanation is true. If two theories are equally good, then we must infer to either both or neither. If assume neither, then we have no theory with which to continue the no miracles argument. But we cannot assume both because they are incompatible, and so to say they are both true would be to state a contradiction.

Here is an example. Consider two or more competing explanations of a crime scene, such as two or more proposals as to the identity of Jack the Ripper. One detective claims that the Ripper was John Pizer, and another that it was George Chapman. The other claims the lover did it and acted alone. Both equally explain the evidence, yet the two hypotheses are incompatible. This, too, is an example of underdetermination.

Underdetermination in Science

However, what matters for our discussion is whether there is underdetermination in science. Is there?

In one sense the answer is "yes," and there is an easy formula to produce it. The formula is the following. Start with any successful theory you want. Call the theory T. Then take any unobservable proposition you want. It could be the proposition,

P:   "There is a beetle that flies around silently just out of everyone's sight, sensation, and all other observational means."

Now consider the following two theories, T+P and T+¬P (where the '¬' sign means "not").

These two theories are incompatible because P and ¬P cannot both be true. They are also equally successful, since they both include all the success of T. So, we have just generated an arbitrary example of underdetermination. (At the University of Pittsburgh, John Earman refered to such an examples as "Kuklaisms" after the philosopher André Kukla who defended them in 1996; early versions of the idea were discussed by Quine in 1975.)

What's wrong with this example? There may be a sense in which it seems artificial. After all, the proposition P (or ¬P for that matter) has nothing to do with the success of the theory itself.

Perhaps one can respond by demanding that only the parts of the theory that are actually responsible for the success appear in the No Miracles argument. Are there examples of underdetermination in which two incompatible claims can both be viewed as equally responsible for each theory's success? The initial equivalence of the Copernican and Ptolemaic systems may be one example.

Such "interesting" examples of underdetermination, if they exist, are much harder to find.

However, even if we do manage to escape underdetermination (and I think it is an open question whether or not we have), scientific realism is not out of the woods yet. Are the other premises of the No Miracles Argument correct? I leave this to you to evaluate. Are there compelling arguments that scientific realism is false?

The problem of the history of science

Imagine you are interviewing a job applicant. How would you decide whether or not to give them the job? What would you look at? You would look at their education, surely, but why — and what else?

If you're sensible, you'll look at the applicant's past experience to see how they did. If an airplane pilot crashed every airplane and parachuted to safety, then you probably wouldn't want to hire that pilot. Past behavior can tell you a great deal about current and future behavior.

So, history matters. If we want to get to the bottom of whether our best existing scientific theories are true, we had better look into some of our past scientific theories to compare!

Unfortunately, this exercise apparently does not to go well for the realist.

Historically false theories

The crystalline spheres theory of astronomy

From ancient Greek time until about the 16th century, the celestial objects visible from the sky were generally thought to inhabit concentric spheres around Earth.

Those spheres slowly rotated at different rates around the earth. The first sphere contained the moon, the fourth contained the sun, and the final sphere containing a "fixed" star field.

These spheres were considered "crystalline" as part of a fundamental separation between "heavens" and "earth" that was thought to exist. According to this separation the earth was fundamentally imperfect, whereas the heavens were fundamentally perfect or "crystalline."

The humoral theory of medicine

Greek and Roman medical theory, encoded by the Roman physician Galen of Pergamon, held that maintaining the body's health was a matter of balancing for different fundamental fluids called humors.

For example, the common cold was caused by too much phlegm, which has a cold and moist quality. One could alleviate the condition by trying to raise one's temperature with hot tea, and by expelling the phlegm as much as possible.

If one had received a cut, the resulting blood was considered to be a "hot" condition, which needed to be cooled. The advice was to pour something cold on it to bring down the temperature.

But you don't want to cool it down to fast with something like water. So, patients were encouraged to cool it down more slowly by pouring alcohol on a wound. The technique proved remarkable successful!

Of course, today this theory is known to be almost entirely incorrect, although it is often still visible in folk medicine. We have learned instead that infectious disease is caused by microorganisms such as viruses and bacteria that are transmitted by touch, consumption, and respiration.

The phlogiston theory of chemistry/combustion

Some things are flammable, and some things are not. The difference, it was thought until the mid-1700's, was that some objects contained more of the flammable element phlogiston, which was just like any other element on the periodic table, except that it caused combustion.

Burning was considered to be a chemical reaction that depleted phlogiston, just as a machine depletes fuel. This explained why burned objects appear to have less mass than they did before they were burned. Some of the matter was literally thought to have been expelled.

However, this theory had trouble explaining a number of important phenomena, like the nature of magnesium. Magnesium is just a metal:

But for this reason, it was thought to have no phlogiston in it, and thus should not be flammable. As it turns out, magnesium does burn at hot enough temperatures. But even worse, it gains mass after burning.

This seemed impossible to explain if burning was just depletion of phlogiston. Today, we understand this happens is because burning is a chemical reaction that involves oxygen, which bonds with magnesium to form a new molecule, magnesium oxide. The magnesium thus appears to gain mass because it has bonded with oxygen.

The electromagnetic theory of aether

Our best theory of electricity and magnetism was developed on the idea that light is an electromagnetic wave. How did people think about this kind of wave?

First, think about a water wave. Water is the substance through which water-waves are transmitted. These waves are just the "up-down" motion of individual particles of water.

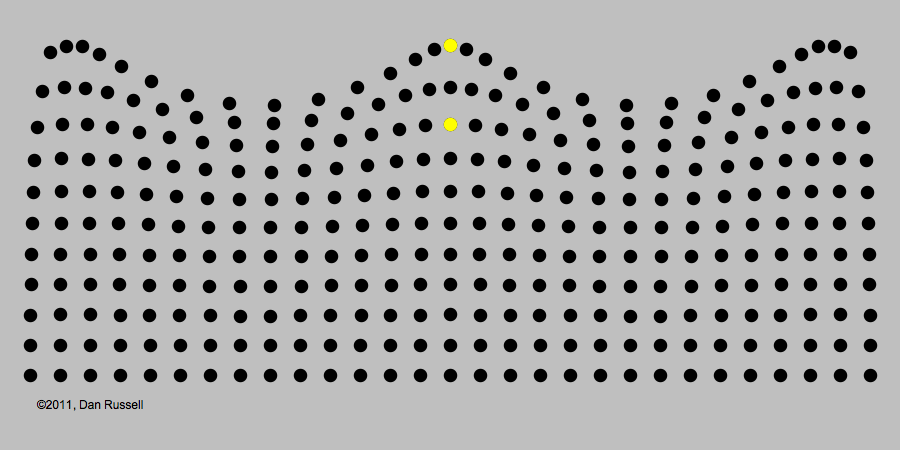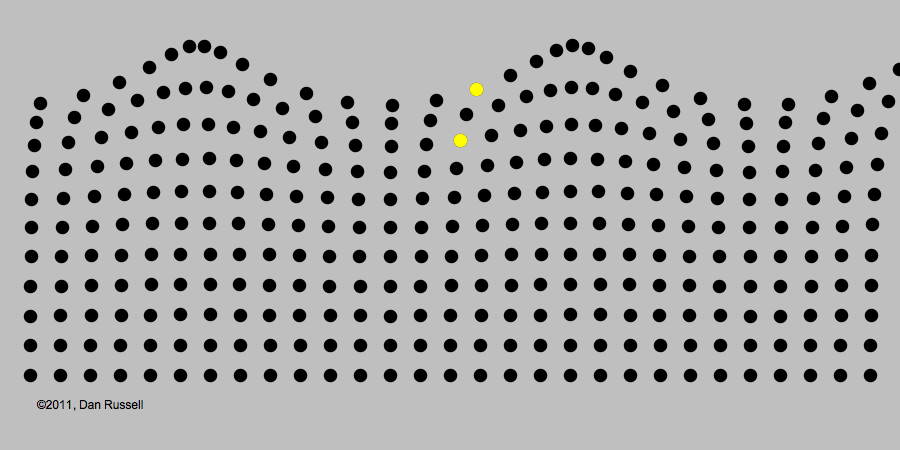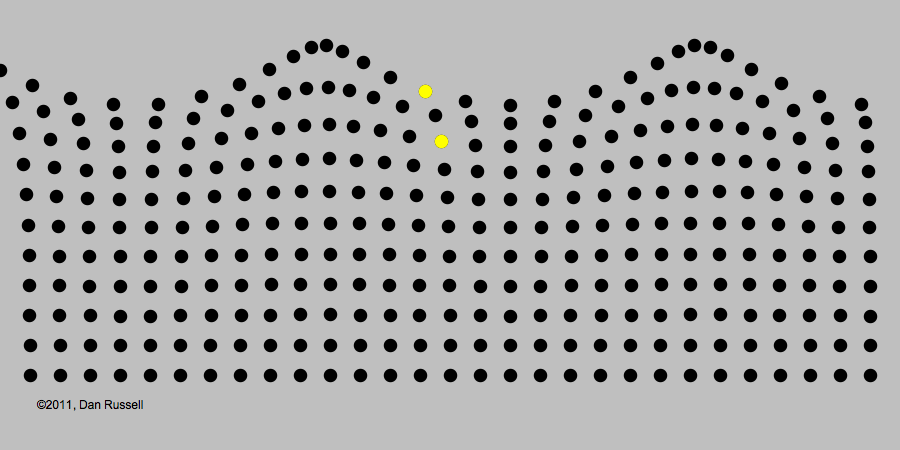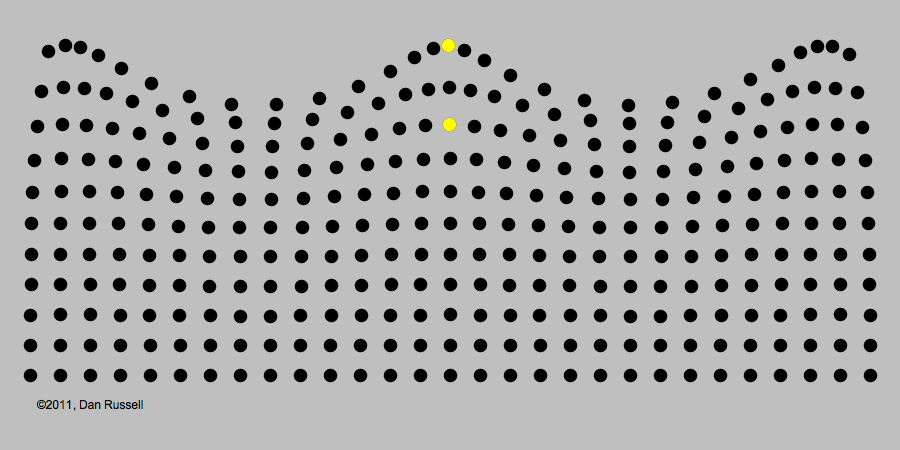
Water-waves only make sense when there is water, which provides the medium for the wave to propagate through.

So, once it was discovered that light behaves like a wave, this was explained by asserting that light-waves travels through a "light-medium," which was called the electromagnetic aether. This thinking led to a great deal of theory being developed to describe the relationships between light, electricity and magnetism in this "aether" medium.

Unfortunately, it turned out that the electromagnetic aether does not exist. Our best theories now require that there is no such thing as aether. Instead, the wave-like properties of light are explained by quantum mechanics.

The Pessimistic Meta-Induction

What do we conclude in the face of all these ill-fated scientific theories? For some, these examples motivate antirealism about the unobservables in science.

Antirealism is the view that we must be agnostic about truth when it comes to the unobservable aspects of scientific theories. All we can say is that the unobservables in our theories are useful instruments that happen to work reliably and successfully. But we do not have any good reason to say whether they are true or false.

Why be an antirealist? The history of science makes a pretty compelling case.

Intuitively, the idea is that after witnessing successful scientific theories fail time after time, we ought to suspect that our current theories will fail as well. Since this conclusion is both pessimistic, and an induction on the history of science, it is often referred to as the pessimistic meta-induction.

However, this is not by itself a good argument. You could ask everyone you meet for your entire life whether or not they're a major lottery winner, and only find people who are not. But this does not imply that major lottery winners don't exist.

However, the argument can be formulated more precisely as follows; this is what we will consider to be the pessimistic meta-induction.

This is a valid argument; in particular, it is a reductio ad absurdum, sometimes called an "argument by contradiction." And this is a more serious difficulty for the realist to contend with.

Genuine Success

One way out of the pessimistic meta-induction is to challenge premise 2. In particular, one might argue that past theories were not really as successful as they are being made out to be here.

For example, the crystalline sphere theory didn't predict much. Although it did provide a model of cosmology, it didn't experience anywhere near the same degree of predictive or explanatory success as modern theories.

Similarly, the humor theory wasn't particularly mature in its success. Although it perhaps had a few more explanatory and predictive successes, it was also extremely primitive and unsophisticated in what it could predict, especially compared to modern germ theory.

So, one realist response is to be more stringent in characterizing genuine success. The types of success that modern science has experienced is much harder to achieve, such as Einstein's prediction of light bending, and the Fresnel-Poisson prediction of a spot in the centre of a shadow.

Thus, a first realist response is to characterize success as requiring both novel predictions and explanations as well as a mature theoretical framework in which to make such predictions and explanations.

The Case of Caloric

Is preservative realism correct? Or, are there examples from history in which even the successful parts were false in some scientific theory?

One potential challenge to the preservative realist story is the caloric theory of heat.

According to this theory, heat was a chemical element, just like oxygen or hydrogen. But the special role of caloric was to produce temperature. So, more caloric meant more temperature. Caloric was thus identified with heat.

There were two main principles about the nature of caloric formed the underpinning of the theory.

First, caloric was self-repelling. So, bunches of caloric didn't want to be near to each other.

This explained why a glass of cold water eventually warms up to room temperature in the summertime. The air in the room had a high density of caloric because it was warm. The ice water had a low density of caloric. So, the caloric in the air repelled away from itself into the glass, causing its temperature to increase.

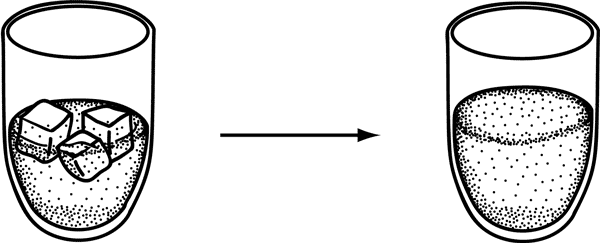
Second, caloric had two states, sensible and latent. When in its sensible state, caloric increased temperature. But when in converted into a latent state, it did not affect temperature, but rather increased volume.

This explained why you get an increase in temperature when you compress a gas.

It was known, for example, that when you put water in a pipe under a lot of pressure, that it heats up. When this happened, hot bubbles would sometimes come to the surface. The explanation was that caloric was being squeezed out of a its latent state, in which it only effected the volume of the water, into a sensible state, in which it increased the temperature.

This idea led Laplace to make the novel prediction that a sound wave should heat up the air. Since the wave is continuously going up and down, the air should get hot as caloric gets squeezed from latent into sensible form. This led him to a dramatically correct prediction of the speed of sound in air.

You can read Laplace's report on this discovery in English here. It really is remarkable that he was able to make such a successful prediction on such curious reasoning!

So, we seem to have a genuine, mature, successful theory in the caloric theory. The only problem is that it is false.

Today, we know that caloric does not have two states. It is not self-repelling. In fact, caloric does not exist. Rather, heat is explained by the motion of particles.

What can the realist say to that? Can realism be saved? More details from the history of science may be required, or a careful analysis of the structuralist or preservative realist options, but for now I leave it to you to decide.