Realism about Unobservables

Bryan W. Roberts
Philosophy, Logic and Scientific Method
Ph103 - Lecture 5

Background Reading: Okasha,
Realism and anti-realism

Introduction to Realism

There is an old question, which was famously asked by Descartes, asking whether any of the external world is real. This idea has been commonly discussed in film as well. Is the world an elaborate dream, as in Inception? Is it constructed by a machine, as in the Matrix? Why think that it's really out there at all?

One of Descartes most famous discussions, the Meditations on First Philosophy, asks this skeptical question. Descartes answered that yes, you can be absolutely sure that the external world is real.

Some of his critics disagreed, like the Irish philosopher Bishop Berkeley, who argued that there is no "external" world; rather, reality consists exclusively of minds and ideas. This view is called idealism.

Both of these views are in a sense a little extreme. It's hard to irrefutably convince the skeptic that the external world is real, and (perhaps harder) to convince someone that their material body doesn't exist.

So, suppose we bracket the traditional realism question. Let us just assume the world is real, to some degree of plausibility. After all, for practical purposes, we all certainly behave that way. (And it is advisable that you continue to do so.) And let's assume further that we come to know about this world through our empirical observations.

Ok, now here's an additional, perhaps even trickier question: can we be realists about the unobservable parts of the world?

Realism about Unobservables

In this discussion, we're not asking that famous question about what it's like when a tree falls in the forest and nobody is around. That's comparatively easy. To answer it, just go hack down some trees and watch what happens. Lots of people have made such observations. We're asking a harder question, of whether we should believe in a hidden reality that nobody has ever seen.

Why would we ever seriously posit the existence of such a hidden reality? Well, because a very authoritative source does so all the time: science. So, this is often called the question of scientific realism: Are the unobservables posited by our best scientific theories true descriptions of the world (at least approximately)?

Of course, when your friend makes up a good story, this doesn't mean you ought to believe it. But we're talking about no ordinary friend, and no ordinary story. Scientific descriptions are some of the most reliable stories you'll ever hear.

Some Dramatic Successes in Science

Science is perhaps one of the most successful enterprises that humans have ever engaged in.

Successful in what sense? I mean success in effectively explaining existing phenomena, as well as succes in prediciting new phenomena. There are lots of dramatic examples of this.

For example, in 1818, a young French engineer named Augustin-Jean Fresnel submitted his theory of light to a competition at the French Academy. This theory proposed that light is a wave, rather than a particle as had been believed since the time of Newton.

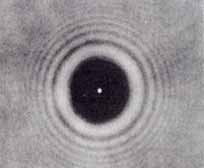
One of the evaluators was the distinguished mathematician Siméon Poisson. Skeptical, Poisson argued that this theory must be false. Although Fresnel himself had not realised it, Poisson showed that the theory made the following seemingly absurd prediction: if you place a very small circular obstruction in front of a light source, then you would see a spot of light right in the middle of the shadow.

To be fair, the head of the committee decided to set up an experiment to check the prediction. To everyone's surprise, including Fresnel himself, the predicted spot appeared clear as day. This was a surprising predictive success for Fresnel's theory. (You can in fact try this yourself using a laser and a coin.)

Another famous success of science is Einstein's prediction that gravity bends light.

Light was well-known to be a quantity that has no mass. Newton's theory of gravity said that only massive objects experience a gravitational force. So, Newton's theory said that light always travels in a straight line in the Euclidean sense.

In 1916, Einstein proposed a radical new way of understanding gravity, which involved positing that spacetime is curved around a massive body like the sun. This led him to predict that light bends when it travels near the sun.

Many were excited to test this very unusual prediction. In May of 1919, British physicist Arthur Eddington took careful photographs during a solar eclipse that Einstein's prediction was correct, and that light really does bend slightly as it travels near the sun.

The shocking success of Einstein's theory quickly made headlines around the world.

No Miracles

Nobody could observe Fresnel's light wave propagating the way we observe water waves propagating. Nobody could see Einstein's curvature in spacetime. However, these theories used these unobsevable descriptions of reality to achieve incredible success in prediction and explanation.

Moreover, these examples aren't so few and far between. Science is chock full of success stories in which unobservable hypotheses are involved in dramatically correct predictions. What are we to conclude from this?

There is a strong intuition that it would be an utter miracle if a theory achieved so much success by coincidence. Such dramatically correct predictions seem to suggest that these theories are actually true, or at least approximately so, even when they describe unobservables.

The argument that makes this intuition a bit more precise is called the no miracles argument. It can be formulated carefully as follows.

No Miracles Argument

We have already discussed how science is successful. Let's talk a little bit about what inference to the best explanation is supposed to be like. Consider the following scenario.

You come home from a late lecture in the evening. You haven't had time to eat, so you're really looking forward to a pizza that you had leftover in the fridge. But to your horror, you arrive to find the pizza missing. You walk into the living room and gasp. Your roommate is sprawled out on the couch, passed out with half-empty beer in hand, and an empty pizza box nearby on the floor.

What might explain why your pizza went missing? Well, there are lots of explanations. Maybe you ate it and forgot about it. Maybe it spontaneously self-incinerated, whilst ejecting the box from the fridge out into the living room. Maybe a pizza ninja stole it and tried to frame your roommate.

But the best explanation of the situation is probably that your roommate got hammered and devoured your pizza. Good reasoning demands that we to infer to this conclusion.

The idea of the no miracles argument is that there is a similar situation with science. Of the many possible explanations of its success, the best explanation is approximate truth. So, the argument goes, good reasoning demands that we infer to this conclusion.

The Problem of Underdetermination

It may not surprise you that there is a major objection to the No Miracles argument. It is called the Problem of Underdetermination.

Recall that the best explanation premise was an essential part of the No Miracles argument. Let's now think a little bit harder about this premise. Is truth (or approximate truth) really the best explanation of success?

The problem of underdetermination is that there can sometimes be multiple incompatible theories, which give equally good predictions and explanations, but none of which are "determined" or "chosen uniquely" by existence evidence.

When underdetermination occurs, one cannot consistently infer that the best explanation is true. If two theories are equally good, then we must infer to either both or neither. If assume neither, then we have no theory with which to continue the no miracles argument. But we cannot assume both because they are incompatible, and so to say they are both true would be to state a contradiction.

Let's go back to the pizza example to illustrate. Suppose you had two roomates, and equal evidence that each got hammered and ate your pizza.

Suppose moreover that you somehow know it that they could not both have eaten it. They might be afraid of each others' germs, say. Then, since there are two equal "best explanations," you can't infer to either one.

Here is another example, which will be familiar if you ever watch crime scene investigator style television. Consider two competing explanations of a crime scene. One investigator claims the butler did it and acted alone. The other claims the lover did it and acted alone. Both equally explain the evidence, yet the two hypotheses are incompatible. This, too, is an example of underdetermination.

Underdetermination in Science

However, what matters for our discussion is whether there is underdetermination in science. Is there?

In once sense the answer is "yes," and there is an easy formula to produce it. The formula is the following. Start with any successful theory you want. Call the theory T. Then take any unobservable proposition you want. It could be the proposition,

P:   "There is a beetle that flies around silently just out of everyone's sight, sensation, and all other observational means."

Now consider the following two theories, T+P and T+¬P (where the '¬' sign means "not").

These two theories are incompatible because P and ¬P cannot both be true. They are also equally successful, since they both include all the success of T. So, we have just generated an arbitrary example of underdetermination. (This is sometimes called a "Kuklaism," after the philosopher André Kukla that first proposed it.)

What's wrong with this example? There may be a sense in which it seems artificial. After all, the proposition P (or ¬P for that matter) has nothing to do with the success of the theory itself.

Perhaps one can respond by demanding that only the parts of the theory that are actually responsible for the success appear in the No Miracles argument. Are there examples of underdetermination in which two incompatible claims can both be viewed as equally responsible for each theory's success?

Such "interesting" examples of underdetermination, if they exist, are much harder to find.

However, even if we do manage to escape underdetermination (and I think it is an open question whether or not we have), scientific realism is not out of the woods yet. Are the other premises of the No Miracles Argument correct? I leave this to you to evaluate. Are there compelling arguments that scientific realism is false? We will see one such argument next week.

What you should know

• The meaning of realism, idealism, unobservables, and scientific realism.
• Some examples of the success of science.
• What the No Miracles argument is.
• Inference to the Best Explanation and how it appears in No Miracles.
• How the problem of underdetermination poses a problem for scientific realism.