The Problem of Induction

Bryan W. Roberts
Philosophy, Logic and Scientific Method
Ph103 - Lecture 7

Background Reading:
Ladyman, Induction and Inductivism,
Rosenberg, Epistemology of Scientific Theorizing, §0-1

Sources of Knowledge

We're going to switch gears now and talk about what we know. But not the content of what we know. We're going to talk about the very nature of knowledge, what it is, and how we come to have it. This is an area of philosophy called epistemology, and we'll be dealing with it throughout the remainder of this course.

There is a famous debate going on in the background of this discussion. It is a debate between two views, known as rationalism and empiricism.

Rationalism is a view that was defended by the great French philosopher René Descartes. You've heard his famous dictum cogito ergo sum, "I think therefore I am," published in his Meditations on First Philosophy in 1641. This inference is an example of how, according to Descartes, certain kinds of knowledge could be acquired through purely rational means.

Rationalism holds that some knowledge is acquired through pure intuition. The precise meaning of "intuition" here is a bit murky. But it is supposed to be a means of acquiring knowledge without the senses. Intuitive knowledge is acquired by just closing your eyes, rationally reflecting, and drawing out knowledge that is independent of one's sensory experience.

On the other side of the ring is empiricism, defended in early forms by British philosophers Francis Bacon and David Hume, pictured on the left and right (respectively) below. Empiricism is the view that the only source of knowledge is through sensory experience, contrary to the rationalist claim.

 

The scientific revolution

A tendency toward empiricism was a central aspect of the scientific revolution, and thus a great deal of success in the acquisition of knowledge. Indeed, the latin word scientia from which "science" is derived literally translates as "knowledge."

During the medieval or "scholastic" era, a driving hypothesis was that a great deal of knowledge had been accumulated by the ancients and then lost. So, the central task of the thinker was to recover knowledge that was lost, especially through the analysis of ancient Christian and Aristotelian texts.

This approach was turned on its head during the scientific revolution, when new thinkers like Galileo Galilei began to give experiments a more central role in their arguments. The image to the right is Galileo's drawings illustrating the first observations of the mountains and valleys and the moon, made possible through Galileo's telescope.

As you know, this approach to acquiring knowledge was a resounding success.

Empiricism is an incredibly successful source of knowledge. But why? How do observations and experience help us form general knowledge about the world? To answer this, we must first understand how empirical knowledge is acquired.

Francis Bacon pointed out that there is a special kind of reasoning that makes general empirical knowledge about the world possible. He called that form of reasoning induction.

Induction: Examples

1. Suppose we want to know if a clock works. I got it from my crazy uncle, and now we want to somehow find out if it keeps time correctly.

We begin by checking that some appropriate background conditions are in place, like the clock has fresh batteries in it, is made by a well-known clock maker, and doesn't have anything obviously wrong with it.

Our next step is to compare it to a reliable standard of time like timeanddate.com:

After observing our clock to give the correct time for several instants, and in a variety of situations, we m ay conclude in general it keeps the correct time. This generalization is an inductive inference.

2. Suppose we want to test Galileo's famous hypothesis that the period of a pendulum's swing depends only its length, and not on the weight of the bob.

One way to do this is to take a reliable clock and time the pendulum's swing under a variety of conditions. We check that for a variety of different weights, and under a variety of different circumstances, the period of the pendulum's swing depends only on its length, and not on the weight of the bob. By induction, we conclude that this is a general property of pendula.

3. Suppose we want to check the florets at the center of a sunflower are arranged in golden spirals.

   

We can check this by observing the arrangement of the florets in many different sunflowers, in many different locations and growing conditions, are all arranged in golden spirals, and conclude inductively that this is a general property of sunflowers. (This property can be viewed as a consequence of an effecient packing algorithm pointed out by mathematician Helmut Vogel in 1979.)

Principles of induction

All of the examples above begin by collecting observations. Then, under the appropriate circumstances, we infer general properties from our observations. These inferences are thus examples of the type of reasoning that we call inductive.

Inductive reasoning or induction is reasoning that infers a general fact on the basis of a collection of observations. Schematically, you can view the structure of our argument involving sunflowers above as follows.

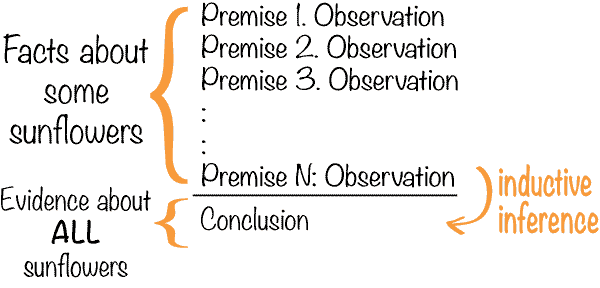
Because of this character, inductive arguments are sometimes called ampliative, in that the conclusion goes beyond the information contained in the premises. This is quite the opposite of what happens in a deductive inference, in which the conclusion can contain no more information than what was already contained in the premises.

When we formulate inductive reasoning as a precise rule of inference, it is called a principle of induction.

One particularly simple such principle is called enumerative induction. This principle says that if we observe a large number of instances in which something has a property, then we can infer that property in general.

Enumerative induction enjoys some limited success. It allows me to successfully predict that it will rain in London in the month of April, and that the sun will rise tomorrow. It has happened many times before, and we can be confident that it will happen again.

... ...

However, enumerative induction does not work in general. For example, I may determine that I have been alive for 10,000 days so far, but this does not provide evidence for the claim that I will live forever. On the contrary, at some point at the end of this sequence I will almost certainly be observed dead.

... ...

This is an instance of a fact that we have seen elsewhere, that the limit of a sequence does not always obtain.

A somewhat more interesting principle is what is known as Naïve Inductivism. This is the view that, if something is observed many times to have a property, and in many different circumstances, and if no counterexample has been found, then one may infer that it has the property in general.

This is just enumerative induction with caveats to make it a bit less susceptible to flaws.

Neither of these principles is completely infallible. There are other inductive principles, some of which we will look at next week, but they aren't infallible either. However, most principles of induction enjoy a great deal of success. And so, the question we must now ask is: why? Why does induction work?

Hume's Problem of Induction

Why do principles of induction work? What justifies the inference countenanced by a principle of induction?

Hume's Problem of Induction is that none of the obvious answers to these questions seem to work. This problem is named after David Hume, who was one of the first philosohpers to explore it. Here are a few attempts to respond to the problem and their difficulties.

Attempt 1: The inductive approach

It is extremely tempting to give something like the following argument.

Inductive attempt to justify induction

  1. Induction worked with the clock.
  2. Induction worked with the pendula.
  3. Induction worked with the sunflowers.
  4. Indeed, we have many observations that induction works, made under a wide variety of circumstances, and with no counterexamples.
  5. Therefore, we have strong evidence that induction works in general.

What's the problem with this reasoning? Think about this for a moment.

Have you thought about it?

The problem is that in order to make this inference, we have implicitly assumed that a principle of induction is true. Otherwise, the conclusion doesn't follow. But then the argument is circular, in that we have assumed exactly what we're trying to prove!

It's a bit like promising to pay someone back the money that you owe them, and then underwriting the contract by promising to keep your promise. There is a sense in which it is a valid argument, but it certainly won't be enough to convince the loan officer!

So, this inductive approach fails to justifiy a principle of induction. So, let us turn to another option.

Attempt 2: The deductive approach

Instead of attempting an inductive argument, we could resort to seeking a deductive argument that establishes a principle of induction. What would such an argument look like?

It is hard to imagine that it could look like anything beyond the following, pointed out by Rosenberg (pg.115).

Deductive attempt to justify induction

  1. If a principle has been reliable on many instances, then it is reliable in general.

  2. Induction has been reliable on many instances.
  3. Therefore, induction is reliable in general.

This of course a valid deductive argument. But it isn't very convincing. Why is the first premise true?

The only conceivable way to answer this question appears to be to resort to inductive reasoning. But that puts us right back to where we started.

A recap

Hume's problem of induction is not what you might have thought. Of course induction isn't as secure as deductive knowledge. Of course we can't be absolutely certain that the sun will rise tomorrow. That's trivially true, and not verly interesting.

What's interesting is that induction usually works. It's still a powerful form of reasoning. It's the form of reasoning underpinning the scientific revolution. And after all, it does provide strong evidence for the claim that the sun will rise tomorrow. It's not absolute certainty, but it's still strong evidence.

The problem of induction comes not from asking why induction sometimes fails, but from asking why induction usually works. The problem is that it's not obvious how to justify this powerful form of reasoning, and the most obvious attempts to do so (deductively and inductively) fail.

Perhaps a budding young philosopher will someday discover a convincing justification for induction, which explains all its successes. Hume himself seemed to think it was just a matter of time. But the problem turned out to be harder than he thought: it's been over 250 years now, and we still haven't reached agreement as to the solution of the problem!

What you should know