Responses to Hume's Problem

Bryan W. Roberts
Philosophy, Logic and Scientific Method
Ph103 - Lecture 8

Background Reading:
Rosenberg, Epistemology of Scientific Theorizing, §0-end,
Popper, A Survey of Some Fundamental Problems.

Assessment of the Problem

We discussed last time how scientific reasoning appears to be characterized by inductive principles. These simple principles turn out to be a very powerful way to reason. That's the good news. The bad news is that, because of Hume's problem, these principles appear to be totally unjustified. Make no mistake: this is a huge problem that has stirred up a heated debate.

If Hume's problem is not solved, then there is a worry that science is undermined. For what else would distinguish scientific reasoning from everything else? Why is science any different than unscientific reasoning, religious reasoning, or just plain arbitrary reasoning? What if anything makes the reasoning of our scientific heroes so special?

               

Today we will discuss several responses to Hume's problem. They fall into two basic types. The first type of of response is to accept our failure to justify induction, and argue that this is not a problem for science. The second is to refuse to give up the search for a justified principle of induction, and instead try to say exactly what such a principle must be like.

Accepting Failure: Popper's Falsificationism

Suppose Hume's problem really does prove that induction is unjustified. Does this mean that we should throw in our cards and be radical skeptics about science? Certainly not. A better alternative is to reject that good science involves induction. Then the failure of induction would do nothing to undermine science.

This is a very clever response, made famous by London School of Economics philosopher Karl Popper. Popper's influence is almost unparalled in 20th century philosophy, extending deep into both natural and social sciences, especially economics.

Popper's reply advises that science (at least, good science) does not and should not proceed by slowly developing stronger and stronger evidence for hypotheses. And it never really gives us reason to believe positive claims like the sun will rise tomorrow, that matter is made of atoms, or any such positive hypothesis. In this sense, Popper advocates a kind of radical skepticism.

What science does do, according to popper, is subject bold conjectures to observation, and discard the conjectures that don't don't match the observations. In short, scientific reasoning about falsifying, not verifying. And if it ever happens that some statement cannot be falsified, then it is outside the domain of good science.

If good reasoning does not involve induction, then there is no problem of induction, and Hume's problem evaporates. According to Popper, we only became convinced there was a problem because we were confused about how scientific reasoning works. For this reason, he calls the problem of induction a pseudoproblem. A pseudoproblem is not a problem that can or should be solved, but is merely an apparent problem that arises out of a misunderstanding.

Popper liked to approach philosophy in this way, by carefully distinguishing legitimate philosophical problems from pseudoproblems. However, it led to a famous kerfuffle with Wittgenstein, a philosopher who believed that all problems in philosophy were pseudoproblems. The story goes that, when Popper was visiting Wittgenstein at Cambridge, a debate between the two became so heated that Wittgenstein menancingly pointed a hot fire poker at Popper, and soon after stormed out of the room. (The further details of the story are controversial.)

Refusing to Give Up: The Logical Response

A more optimistic kind of response to Hume's problem is to take the attitude that although a justified principle of induction has not yet been found, we may yet discover one. But to make good on this claim, one must ideally produce such a principle, or try to.

The most famous class of attempts treats inductive reasoning as a special class of logic. Once we discover the rules for this logic, we will have discovered the inductive principles that are correct. This can be called the logical response to Hume's problem.

How might that logic work? It's easiest to see with an example.

Before 1846 only seven planets were thought to exist in the solar system, with Uranus being the most distant one. However, it had been known for decades that the orbit of Uranus did not seem to match the predictions of Newton's theory of gravitation. So, a French mathematician named Urbain Le Verrier hypothesised an additional planet just beyond Uranus giving rise to the anomalous orbit.

To test his hypothesis, Le Verrier observed that if his hypothesis were true, then this would imply that the new planet had to have a particular precise location, which Le Verrier was able to calculate. When astronomers looked to see if there was anything there, they were shocked to find that he was right! Le Verrier became famous as the man who discovered a planet with the point of his pen.

In more general terms, this rule for inductively inference is the following.

The Hypothetico-Deductive Method

  1. Propose a hypothesis.
  2. Show that the hypothesis implies a testable prediction.
  3. Check whether the data matches that prediction.

If the data matches, then we can say that the hypothesis is (inductively) confirmed. If not, then we can say that it's falsified.

This approach is sometimes called the hypothetico-deductive method of confirmation. It is also typical to call this kind of procedure the "scientific method" in school textbooks. And it is the simplest of the logical responses to Hume's problem.

The Paradox of the Raven

The philosopher Carl Hempel pointed out that this simple expression of induction has a serious problem, now known as Hempel's Paradox of the Raven. This problem, quite simply, utterly destroys the simple characterisation of the scientific method commonly appearing in gradeschool textbooks.

The paradox begins by recalling the initial logical response to Hume's problem. We begin by formulating a hypothesis, and choosing some statement that we can test that is logically entailed by our hypothesis.

For example, suppose we are interested in testing the hypothesis, All ravens are black. This hypothesis logically entails the statement "If something is a raven, then it's black." So, we only need to go out and check some ravens to see if they agree with the statement that

By encountering a raven that is black, we confirm that the statement, "If something is a raven, then it's black" is true. According to the logical response, this provides evidence for the statement that "All ravens are black."

You may find this similar to what you might have called "The scientific method" in school. The trouble is, it doesn't work. By the same reasoning, we could use all kinds of crazy observations to provide evidence for our hypothesis, but which clearly have nothing to do with it.

Go back to our hypothesis that all ravens are black. It also logically entails the statement, "If something is not black, then it's a non-raven." There are many observations that we can use to confirm this statement. A white shoe, a banana, a football — all of these objects confirm that not-black things are non-ravens.

According to the logical response, these observations all provide evidence for the hypothesis that all ravens are black, for the same reason that a black raven does. But this is absurd! A white shoe has nothing to do with the hypothesis. Nor does a banana, nor a football. These observations do not confirm the hypothesis that all ravens are black. Something has gone horribly wrong.

Hempel used this example to illustrate that they logical response to Hume's problem is too simple as it is originally proposed. A more refined kind of logical response is needed.

A new riddle: Grue and Green

Once Hume's problem is solved, there remain further problems with induction. One of the most famous ones is called Goodman's New Riddle, posed by Nelson Goodman in Fact, Fiction and Forecast.

Goodman argues that no principle of induction can give us reason to believe a general hypothesis on the basis of particular observations. If there were such a principle, then it would lead us to believe in contradictory things.

For example, consider the hypothesis, All emeralds are green. Suppose that it is possible to confirm such a hypothesis using only our observations. They could be observations about emeralds, crystal formation, geothermal physics — whatever. But some principle of induction allows us to confirm that all emeralds are green.

Now we're going to define a new property, called "grue." An emerald is "grue" if it looks green in color until the year 2024, at which point it suddenly starts to look blue in color. Otherwise, a grue emerald is exactly like a green emerald. And in particular, the two are totally indistinguishable until the year 2024. Then suddenly their differences will appear.

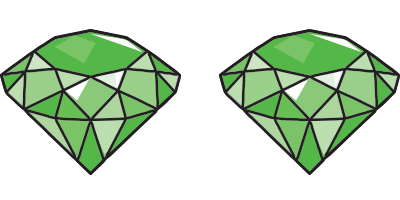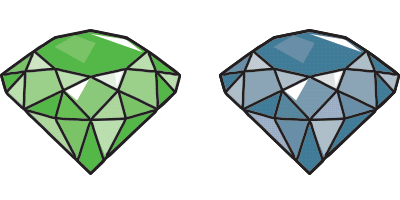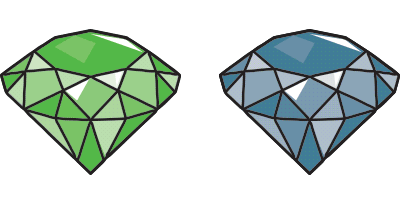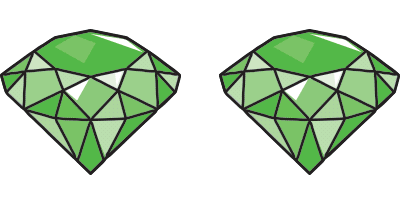
The problem is that our observations are all prior to 2024, and the facts about grue emeralds and green emeralds agree up to that point.

As a result, it would appear that all our observation confirming emeralds are green also confirm they are grue. That is, a principle of induction that allows us to infer "All emeralds are green" equally (it seems) allows us to infer that "All emeralds are grue."

But the statements "All emeralds are green" and "All emeralds are grue" are contradictory claims. They cannot both be true! Thus, it appears that we are in the very embarassing situation of finding that a principle of induction allows us to infer a contradiction, no matter how we formulate it.

This is not the end of the story. Can you think of any objections to Goodman's argument?

One concern is that Goodman's story about green and grue emeralds requires indeterminism. Part of the story is that there is really no amount of past information that would distinguish between green emeralds from grue ones before 2024. In other words, this assumes that our best theories of emeralds are indeterministic.

It is quite possible that our best theories of emeralds are indeterministic. However, determining whether or not this is the case would require considerable analysis of the nature of emeralds tha thas not been carried out yet. So, since this formulation of the grue-green problem requires indeterminism, it is not clear that grue-green scenarios are really possible.

What you should know