The most beautiful science
 Mathematics is a beautiful way to think. It's full of some of the most wonderously ornate constructions that that the human mind has ever managed to entertain.
Mathematics is a beautiful way to think. It's full of some of the most wonderously ornate constructions that that the human mind has ever managed to entertain.
 Mathematics is also often considered an example of the purest kind of rational thinking. In this sense, it is no surprise that philosophers have long studied the nature of mathematics. Understanding mathematics is an important way to understand the nature of rationality.
Mathematics is also often considered an example of the purest kind of rational thinking. In this sense, it is no surprise that philosophers have long studied the nature of mathematics. Understanding mathematics is an important way to understand the nature of rationality.
Today, we are going to talk about what makes mathematics so special.
Certainly, part of what's special is the incredibly broad applicability of mathematics. Galileo was so impressed by this that he was led to say that natural philosophy (or science, in modern language) is "written in the language of mathematics.'' It makes an indispensible appearance in almost every field of knowledge, from physics to biology to economics.
But another part of what's special about mathematics is mathematical proof, the unique way of justifying mathematical claims.
Since the concept of a proof will be central to our discussion, we will need to introduce an example of one. But first, let's introduce the question that it's about: the nature of the number \(\sqrt{2}\).
\(\sqrt{2}\): a 2,000 year old question
The number \(\sqrt{2}\) was first studied by the ancient Greeks. So, you aren't going to need any fancy mathematical abilities to understand it. How did the Greeks come to think about this number? Here's a way they might have done it.
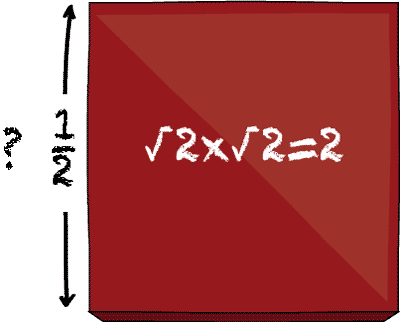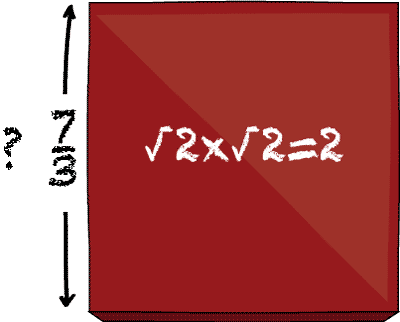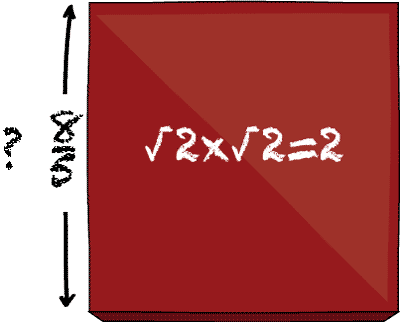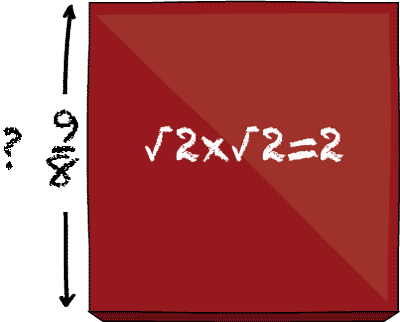
Suppose a painter is painting large and small square tiles. It happens that a small tile with a side-length of 1cm requires exactly 1g of paint to cover. And, a large tile with a side-length of 2cm takes 4g to cover.
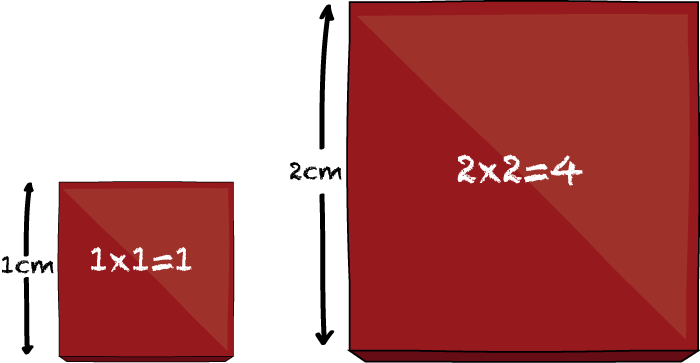
One day, the painter finds a medium-sized tile, and notices that it takes exactly 2g of point to cover. Since she's always been fascinated by mathematical questions, the painter asks: what is the side-length of this new tile
Whatever it is, we'll call that number \(\sqrt{2}\). It is a number that, when multiplied by itself, is equal to the number 2.
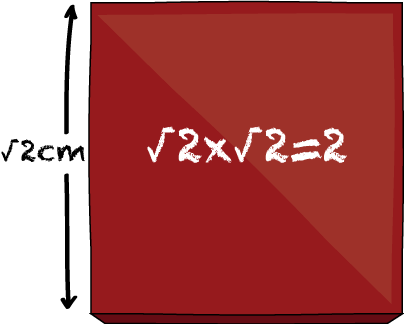
Now, here is the 2,000 year old question. Whatever the value of \(\sqrt{2}\) is, can we write it down as a fraction — that is, as the ratio of two whole numbers? That is, we want to know if we can find two numbers \(a\) and \(b\) such that \(\sqrt{2} = \frac{a}{b}.\)
A number is called rational if it can be written as a fraction in this way; otherwise, it is called irrational. So, another way to put our question is this:
Is \(\sqrt{2}\) rational or irrational?
The beauty of proof
How do we provide answers to mathematical questions like this? We do it using a mathematical proof.
 Proofs provide an absolutely beautiful way to understand something. Their aesthetic character has long been known. The philosopher Bertrand Russell, who was somewhat of a mathematician himself, said of the Cambridge mathematician G.H. Hardy the following:
Proofs provide an absolutely beautiful way to understand something. Their aesthetic character has long been known. The philosopher Bertrand Russell, who was somewhat of a mathematician himself, said of the Cambridge mathematician G.H. Hardy the following:
He told me once that if he could find a proof that I was going to die in five minutes he would of course be sorry to lose me, but this sorrow would be quite outweighed by pleasure in the proof. I entirely sympathized with him and was not at all offended.
Here is an example of a particularly elegant and beautiful mathematical proof, which also provides an answer to our question about whether \(\sqrt{2}\) is rational.
Theorem. \(\sqrt{2}\) is irrational.
Proof. Our strategy is to show that if \(\sqrt{2}\) is rational, then this implies a contradiction. From this we can conclude that \(\sqrt{2}\) must be irrational.
Suppose \(\sqrt{2}\) is rational, so that we can write \(\sqrt{2} = \frac{A}{B}\) where \(A\) and \(B\) are integers. All such fractions can be written in lowest terms \(\sqrt{2} = \frac{a}{b}\), where \(a\) and \(b\) are integers with no common factor. We will rewrite this equation by squaring both sides to get \(2 = \left( \frac{a}{b} \right)^2 = \frac{a^2}{b^2}\). Multiplying both sides by \(b^2\), this says that \(2b^2 = a^2\).
Now, an integer \(n\) is even just in case we can write it as \(n = 2m\) for some \(m\). For example, \( 6 = 2 \times 3\), \( 10 = 2 \times 5\), etc. So, what we found above is that the number \(a^2\) is even. But a square like \(a^2\) is even only if \(a\) is even, since squaring an odd number always produces an odd number. (Notice that \(3^2 = 9\), and \(5^2=25,\) etc.) So, we can write \(a = 2c\) for some integer \(c\). Substituting, this implies \(2b^2 = a^2 = (2c)^2 = 4c^2\), which reduces to \(b^2 = 2c^2\). But this says that \(b^2\) is even, and hence that \(b\) is even as well.
Since both \(a\) and \(b\) are even, they have a common divisor, namely 2. But we assumed at the outset that \(a\) and \(b\) do not have a common divisor. So, we have reached a contradiction. We therefore reject our original hypothesis that \(\sqrt{2}\) is rational, and conclude that \(\sqrt{2}\) is irrational. QED.
The great puzzle of philosophy of mathematics
If this was your first time reading this proof, then an amazing thing just happened in your brain: you learned something. Now, how did that happen? Of course it's because we gave a particular kind of argument known as a proof. But how is it that the style of argument above led you to know that \(\sqrt{2}\) is irrational, when you didn't know before?
Or, to put the question another way What is the source of justification for mathematical truths? This is the great puzzle of the philosophy of mathematics.
With physical facts like Newton's law of gravity, the source of justification is empirical observation. But it appears that observation was not the source of knowledge when you learned that \(\sqrt{2}\) is irrational. So, what was it?

Knowledge justified through empirical means is known as a posteriori knowledge, whereas knowledge justified through any other means is known as a priori knowledge. So, the puzzle can be restated yet again in this way:
If mathematical knowledge is a priori, rather than a posteriori, then it is not clear what the source of a priori knowledge is.
Notice that this is question not about knowledge acquisition. Empirical experience is of course part of how you acquired knowledge of the irrationality of \(\sqrt{2}\), in that you read or heard the words of the proof.
But that's just how you happened to acquire knowledge the mathematical truth, not what justifies it. Indeed, clever philosopher that you are, you might very well have conceived of this proof all by yourself and entirely in your mind, which is to say non-empirically. And yet (it appears) this would still be enough justify the mathematical truth.
In Lecture 7 we discussed empiricism. We can now distinguish a modest and a radical form of empiricism. According to the modest form, empiricism expresses the view that facts about the physical world are a posteriori. This is a very common view. In its more radical form, empiricism expresses the view that all facts are ultimately a posteriori. This is a more radical view, which is difficult to justify in the face of mathematical facts that appear to be a priori.
The platonist response
The first response to this problem is a view that we will call platonism. It is the analogue in the philosophy of mathematics of scientific realism, discussed in Lecture 5. The platonist view is that, just as empirical reality is the source of a posteriori truth, so mathematical reality is the source of mathematical truth.

This position has two aspects. The first is ontological, meaning that it is about the nature of what exists. This is an aspect of platonism which says that although mathematical objects do not exist in space and time, they still exist. Mathematical objects (perhaps like \(\sqrt{2}\) are just as real, and mathematical facts just as true, as objects and statements in the empirical world.
The other side of the position is doxastic, meaning that it is about what we believe. Mathematical reality determines what we ought to believe. In particular, mathematical truths are the kinds of things that we come to believe and know about through the special practice of mathematical proof.
The platonist response does very well at explaining what the source of mathematical knowledge is, and especially why it is so compelling. But it has at least two difficulties.
The first is how we could possibly have access to such a non-empirical aspect of reality. Our sensory access to the world, and even the way our brains process those sensory perceptions, seem rooted in empirical processes. How is it that we come to detect facts about a supposedly non-empirical aspect of the world?
The second difficulty is that, given the separation between mathematcal and empirical reality, it is enormously puzzling why mathematics is so effective in describing empirical phenomena. We noted above that mathematics has applications in almost every area of human thought. Often these applications are unexpected. This led the physicist Steven Weinberg to say,
"It is positively spooky how the physicist finds the mathematician has been there before him or her."
Thus, although the mathematical platonist has a good explanation of the source of mathematical truths, as well as why those truths are so compelling, the story is less convincing when it comes to our access to those truths and our ability to apply them.
The mathematical antirealist response
If these difficulties are insurmountable, then one may be led to adopt the mathematical antirealist response to the problem. This view asserts that there is no special, mind-independent aspect of reality corresponding to the mathematical realm. The source of mathematical truths is the same as the source of any other truths.
 From this point, mathematical antirealists respond to the puzzle of philosophy of mathematics in different ways. For example, one form of mathematical antirealism is to be an idealist, or a denier of reality beyond the constructs of human thoughts (also discussed in Lecture 5. On this view, there is no mind-indepenet aspect of reality at all, mathematical or otherwise.
From this point, mathematical antirealists respond to the puzzle of philosophy of mathematics in different ways. For example, one form of mathematical antirealism is to be an idealist, or a denier of reality beyond the constructs of human thoughts (also discussed in Lecture 5. On this view, there is no mind-indepenet aspect of reality at all, mathematical or otherwise.
A less radical form of mathematical antirealism, advocated by the great 20th century mathematician David Hilbert, is the conventionalist view of mathematics.
The conventionalist approach to mathematical antirealism treats mathematics like the game of chess. The rules of chess are conventional. They are an entirely human invention, which could have been very different. Nevertheless, the rules of chess are very strict, allowing only certain kinds of play. It also guarantees certain facts to a high degree of certainty, such as the fact that certain attacks or defenses are possible.
The conventionalist treats mathematics as a similar kind of invention: just as humans invented chess, they also invented mathematics. At the same time, the rules of mathematics are still very strict, and allow only certain kinds of reasoning, which is very trustworthy.
The conventionalist approach to mathematical antirealism accomodates the radical empiricism discussed above. In particular, the conventionalist is able to view mathematical truths like 2+3=5 as a posteriori. However, this does not imply that the ultimate justification of mathematics is through inductive inference on observational evidence. We don't justify 2+3=5 by observing many successive combinations of 2 and 3 objects.

Even for the conventionalist, the justification of 2+3=5 is that it follows from a rule of arithmetic. But the justification of that rule, according to the conventionalist, is that humans have pervasively agreed to adopt it as a matter of convention. No further justification is needed.
It is in this sense that conventionalism views the ultimate source of justification for mathematical truths to be empirical, and therefore views mathematical truths as a posteriori, in spite of appearances to the contrary.
Benacerraf's Problem
Platonism and mathematical antirealism highlight a difficult tension between metaphysics and epistemology in the philosophy of mathematics.
Mathematical truths are the kinds of statements that are both certain to a high degree and also easily knowable by humans, through the practice of mathematical proof. Each of these aspects of mathematical truth is explained by one of the two views above but not the other.
Platonism explains the certainty of mathematical truths with ease: it is because they describe a special mathematical reality. But it does not seem to provide an account of how we come to know those truths.
On the other hand, conventionalism explains the knowability of mathematical truths with ease: mathematical truths are just consequences of rules invented by humans. But it does not seem to explain why mathematical truths appear to be so certain.
This general tension can be summarised: the more metaphysical significance we give to mathematical truth, the less epistemological access we allow; and the more epistemological access we allow, the less the metaphysical significance. This is known as Benacerraf's problem, after the Princeton philosopher Paul Benacerraf who first proposed it. (Original article here.)