Three big ideas
Once you've understood the concept of a random walk, we can immediately introduce three more big ideas that will allow us to put it to powerful use, both in physics and in finance:
- The atomic hypothesis; and
- The diffusion process.
- The microscopic-macroscopic connection.
The first person to realise the predictive power of these ideas was no less than Einstein himself. In fact, they appeared in no less than three of his most important discoveries. We will see how they appear in two of them now, as the first practical use of these ideas together. Later we will see how this same thinking gave rise to a revolution in finance as well.
Einstein's Miracle Year
Cornelius Lanczos, one of Einstein's assistants in the 1920s, later said about him:
"if somebody asked: 'Who is the greatest modern physicist after Einstein?' the answer would be: Einstein again. And why? Because although the theory of relativity in itself would have established him fame forever, had somebody else discovered relativity, his other discoveries would still make him the second greatest physicist of his time."

Albert Einstein in 1904, photographed by the Swiss patent office where he worked.
The year of 1905 is known as Einstein's Annus Mirabilis or Miracle Year. It doesn't happen often that somebody publishes a work that fundamentally changes the course of science. You've probably heard of one that Einstein published in 1905, the theory of special relativity (especially if you've taken my course on Einstein). But that's not the reason it's called Einstein's Miracle Year. It's because Einstein published no less than five papers that fundamentally changed science.
Here they are in one logical order that Einstein might have written them in. If you're curious, you can follow the link to read the paper itself.
- 1. Einstein's Dissertation. "A New Determination of Molecular Dimensions", Buckdruckerei K. J. Wyss, Bern, published 30 April 1905. Original Dissertation English Translation
- 2. Brownian Motion. "On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat", Annalen der Physik, published May 1905 (received 11 May 1905). English Translation
- 3. The Light Quantum. "On a heuristic viewpoint concerning the production and transformation of light", Annalen der Physik, published 17 Mar 1905. English Translation
- 4. Special Relativity. "On the electrodynamics of moving bodies", Annalen der Physik, published 30 June 1905. English Translation
- 5. E=mc2. "Does the Inertia of a Body Depend Upon Its Energy Content?" Annalen der Physik published 21 November 1905. English Translation
Puzzle 1: For which paper did Einstein win the 1921 Nobel Prize in Physics? Give it a guess if you haven't heard the answer before.

The last two papers seem like good candidates: together, they establish the theory of special relativity, for which Einstein is perhaps best known. We studied this in the first part of Einstein for Everyone. However, neither of those papers won Einstein the prize.
The remaining papers are statistical in nature, and are all relevant to our discussion of physics and finance. And it is one of these papers, Einstein's paper on the light quantum, for which he was awarded the Nobel Prize. This paper turned out to be a fundamental building block in the discovery of quantum mechanics; we will discuss it more next week.
Puzzle 2: Which of Einstein's Miracle Year papers is the most cited? Here again a good candidate would seem to be one of the special relativity papers, or perhaps the light quantum paper, or maybe even the Brownian motion paper. Go here to read about the answer: Which is the Most Cited of Einstein's Papers of 1905? It is Einstein's doctoral dissertation, which has become the starting point for the modern analysis of viscosity. If you're curious, have a look at some of the articles and books citing Einstein's dissertation.
The thinking in Einstein's dissertation involved reasoning about atoms and diffusion, which tied together all his statistical papers from 1905. It is this powerful way of thinking that led to the first modern analysis of Brownian motion in physics. It also led him to the invention of quantum mechanics, and plays a role in the analysis of financial systems as well. So, it is worth spending the time to understand it!
Atomic thinking
The concept that formed the backbone of Einstein's statistical thinking was the atomic hypothesis. Below is an image of several individual atoms in graphene, imaged by researchers at the University of California, Berkeley in 2008. The little grey dots indicated by red arrows are individual hydrogen atoms. The black dots are carbon atoms. This is a truly remarkable achievement: it has only been possible to "image" atoms in this way for about 10 years.
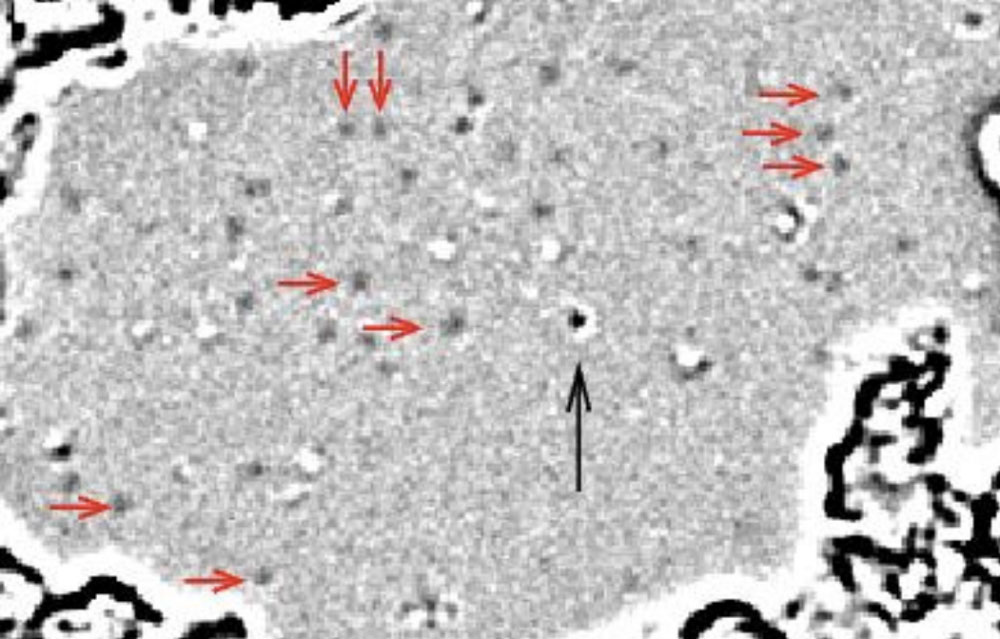
Hydrogen and carbon atoms in graphene, from Meyer et al. (2008)
To appreciate how difficult it was to take this picture, you have to recognise that atoms are really small. How small? Here is an exercise to illustrate. But a rough rule of thumb to help you remember is: if you consider were to take an apple and magnify it so that it is the size of the earth, an atom would be the size of the original apple.
Our world wasn't always understood in atomic terms. Until the beginning of the 20th century, many believed that that every fundamental substance was a continuum, which could in principle be zoomed in on forever without reaching a most basic part. For example, here is what a copper thread might look like if it were a true continuum.

Once we do posit the existence of atoms, it has wide-ranging consequences. The physicist Richard Feynman suggested that, if all scientific knowledge were destroyed, and only one sentence could be passed on to future thinkers, that sentence should be the atomic hypothesis:
The atomic hypothesis. All things are made of atoms — little particles that move around in perpetual motion, attracting each other when they are a little distance apart, but repelling upon being squeezed into one another.
The atomic hypothesis implies that everything, from the sloshing tides of the river Thames, to the complex workings of a human eye, are all ultimately the result of interacting atoms. The possibilities associated with these little objects are immense.

A complex arrangement of atoms. Image credit: J. J. Harrison
One familiar consequence of the atomic hypothesis is the phases of matter. When atoms become close together, they attract each other and form a solid. You can't press them too close together though, or they repel. This gives matter its solid feel. When those atoms have a little more energy, they can break out of this interlocking grid and become a liquid. The liquid can flow around, but it still keeps a fixed volume because of the attractive force of the atoms. The jiggling motion of the atoms is part of what we call heat. When there is enough of it, the atoms can break apart further and become a vapour.
We have only just scratched the surface of what is implied by the atomic hypothesis. We will soon see even more that can be derived from it.
Diffusion
Our second big idea, after the atomic hypothesis, is the concept of diffusion. You have experienced diffusion many times before. It happens every time you add milk to tea, or ink to a jar of water as in the image below.

A diffusion process: Ink diffusing in water
What is the underlying mechanism that gives rise to diffusion, from the perspective of the atomic hypothesis? In the case of the ink dropped in a jar of water, it is due to the fact that the ink consists in a jumble of atoms, with velocities roughly uniformly distributed in every direction. Of the possible states ink might be in, it is extraordinarily likely that they are in some configuration that will spread out into the jar.

However, in practical terms, we don't know the exact positions and velocities of the 1024 particles in the glass of water, and so it is difficult to predict their behaviour on this basis. However, there is another, much simpler alternative.
The random walk model
Suppose we presume a helpful fiction. Suppose that the particles in a glass of water are following a random walk. Each particle takes a little step in one direction, with each direction equally likely, and with each step completely independent of the previous. Imagine that a collection of ink molecules dropped in a jar of water behaved like that.
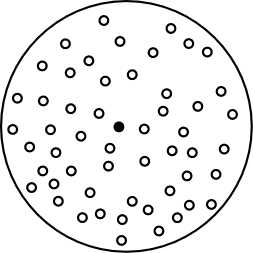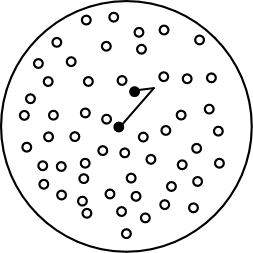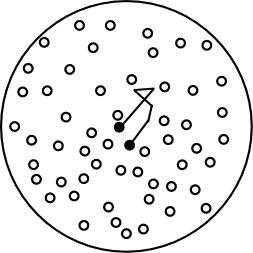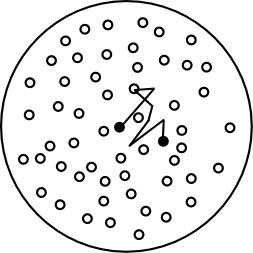
Randomly walking particles. Image credit: John D. Norton
Since the motion is modelled by a random walk, we learned last time that we can expect the particles to be normally distributed away from their starting point. So, for example, when we drop ink in water, we know that it will tend to cluster around its starting point, but that it will spread out more and more over time. That is, the random walk model gives rise to diffusion. It can be used to model the large-scale behaviour of the ink in the jar of water, a small in the room, or any other diffusion phenomenon.

Diffusion via random walk.
Notice that, from a macroscopic perspective on the gas as a whole, diffusion via a random walk gives rise to exactly the same thing as the image of diffusion via a deterministic process. Nevertheless, from a microscopic perspective, these two animations clearly describe very different things.
Models and Fictions
The sorts of descriptions we have been talking about so far are sometimes referred to in science and philosophy as models. But what kind of thing is a model? What makes a model correct or incorrect? How do we learn from models?
A common response is that a model is a construction that shares structure with the thing it represents. It is correct to the extent that it accurately shares this structure. This is the idea underpinning a view called the structuralist account of models.

This is often called the `models' or 'semantic' view of scientific theories. A classic proponent is Patrick Suppes; a more recent description of the view has been defend by French and Ladyman (1999). A canonical statement of it can be found in van Fraassen's (1980) Scientific Image, as quoted by French and Ladyman:
"To present a theory is to specify a family of structures, its models; and secondly, to specify certain parts of those models (the empirical substructures) as candidates for the direct representation of empirical observable phenomena. The structures which can be described in experimental and measurement reports we can call appearances: the theory is empirically adequate if it has some model such that all the appearances are isomorphic [meaning, share the same structure] to empirical substructures of that model. (van Fraassen 1980, p.64)
Can a random walk description be understood on the semantic view? This is not so clear. On the one hand, the random walk model does accurately describe the macroscopic behaviour of diffusion phenomena, like the ink droplet in water, or Einstein's viscous liquids. As far as macroscopic descriptions go, the random walk model is 'isomorphic' or structurally identical to the phenomenon observed in the real world.
On the other hand, an essential feature of the random walk model appears to be that it inaccurately describes microscopic phenomena. Here, there is no isomorphism. In random walk models, we embrace our ignorance, and make the powerful step of entering the fact that we don't know what the microscopic particles are doing into our model. So, instead of adopting a deterministic description, which would more correctly match the structure of our system, random walks work by describing the microscopic components randomly. This kind of failure is actually a virtue for us, since we would be unable to use a model that requires precise descriptions of the underlying molecules. And it works incredibly well, because the large-scale, average predictions of the model are still correct.

Deterministic model: Microscopically accurate, but intractable for practical use

Random walk model: Microscopically inaccurate, but tractable and still macroscopically correct
Perhaps the 'partial structures' account of French and Ladyman might help. On their account, a theory need only partially describe reality in order to be accurate. However, something still appears to be missed: in the random walk model, it appears that the inaccuracy of randomness is somehow an essential part of what makes the model work. The partial structures account appears to have nothing to say about why this is.
If the semantic account fails to correctly describe how random walk models represent the world, then what is the alternative? One account of interest is the view of models as fiction, developed by Roman Frigg and others. On this view, a model is very much analogous to works of literary fiction: it can contain facts relative to the fiction, even if they are ultimately false, and which are still useful for some purposes.
On Frigg's view, scientific models treated as fictions require additional qualifications that distinguish them from literary fiction. A remaining question is whether this account of models is sufficiently informative to allow us to understand the predictive success of the random walk model.
Ideal Gases: A microscopic-macroscopic connection
Let's begin to apply these ideas now. Think about what would happen if we were to confine our gas inside a container, with a lid on top to keep it in, from the perspective of the atomic hypothesis.
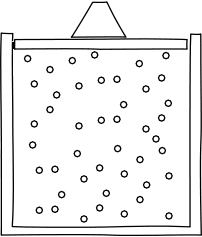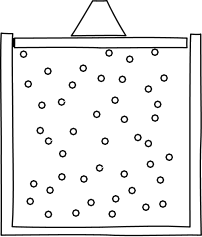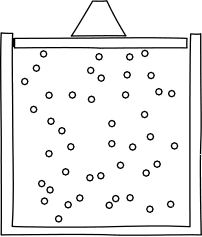
Image credit: John D. Norton
In any given moment, there would be a certain number of atoms slamming into the lid. It would thus take some force to keep the lid from flying off. So, the atomic hypothesis suggests a gas will give rise to a force per unit area from the slamming into their container. This is called pressure.
Pressure, volume and temperature are all macroscopic quantities. Unlike atoms, they are easy to observe on the ordinary scale of medium-sized objects. You're familiar enough with volume and temperature. And you experience pressure changes when you go up in an elevator or airplane and feel your ears popping.
How exactly are the laws governing these macroscopic quantities related to the microscopic atoms that make them up?

We can draw on more of the ideas we've learned so far. For example, suppose we double the number of particles. We assume that they won't clump or repel each other, so the net effect of this is just that there are twice as many particles slamming into the lid. So, for a fixed temperature and volume, the pressure increases with the density of particles when the particles are independent of each other.
Through similar reasoning from the atomic hypothesis, one can also observe that a gas has each of the following properties.
- Pressure goes with temperature. When all else is equal, an increase in temperature corresponds to an increase in pressure, since this amounts to faster-moving particles, which give rise to more energetic collisions with the container lid.
- Pressure goes inversely with volume. When all else is equal, an increase in volume corresponds to a decrease in pressure, since more space for the particles to move around in leads to less collisions with the lid.
See if you can say why this is in precise terms, thinking in terms of the image of a container of gas above. There is really a great deal that one can establish from this one simple hypothesis.
It turns out that one can summarise these results with a remarkably simple law. If the motions of particles in a gas are described by a random walk, then the following law holds:
\[ PV = NkT, \] where P is pressure, V is volume the gas occupies, T is temperature, N is the number of molecules in the gas, and k is a constant. This equation is known as the ideal gas law.Although the law itself had been known since the 1830's, was only later realised that it has a particularly nice expression in terms of the atomic description of matter. The relationship goes two ways:
1. Independent atoms → Ideal Gas Law. If a system is described by a large number of atoms jiggling about in such a way that each follows a random walk independently of the others, then the pressure, volume and temperature of that system is described by the Ideal Gas Law.
We developed a feel for why this is in our atomic reasoning above. But the converse also holds:
2. Ideal Gas Law → Independent atoms. If a large number of atoms jiggling about according to a stochastic rule are described by the Ideal Gas Law, then the motions of those atoms are mutually independent of one another.
Optional: Comments on the Derivation
This simple connection between macroscopic and microscopic descriptions is what drove Einstein's thinking in all three of his statistical papers, beginning with his dissertation.
The result also has incredible consequences: the ideal gas law does not depend on the kind of substance that makes up the gas. In contrast, the laws governing how a substance conducts electricity, or those governing its crystal structure in solid form, all depend greatly on the kind of substance involved. But to obey the ideal gas law, a substance only has to consist in atoms the move independently of one another. It is general enough to hold of liquids and gases of all different kinds.
Application 1: Einstein's PhD dissertation
What was Einstein's dissertation about? Einstein wanted to understand the size and number of molecules dissolved in a liquid. His dissertation was titled, "A New Determination of Molecular Dimensions".
Sound a little dry? There is a reason. Einstein had a very conservative supervisor, Alfred Kleiner, who seems to have demanded extremely meticulous work that avoided bold claims. Einstein, full of bold ideas, had such a falling out with the supervisor that at one point he considered giving up on the PhD, although in the end he changed his mind and finished. The first draft of his dissertation (which is unfortunately lost) actually didn't pass, and Einstein had to rewrite it!
Einstein's dissertation began with the observation that, when you dissolve a lot of sugar in water, it increases the viscosity or thickness of flow. Einstein proposed that this is because the water has to flow around all these tiny obstructions, the sugar molecules.

Using the analysis of how liquids flow around obstructions, Einstein argued that the size and number of molecules stand in a relatively simple relation. If we idealise the molecules as spheres of radius \(R\), then the number of molecules \(N\) in the sugar solution is given by,
\[N = c \times 1/R^3,\]where \(c\) is just a constant that depended on the viscosity of the liquid, which Einstein knew the measured value of. This determined a relationship between the number and size of molecules dissolved in sugar. The problem was that he still didn't know the value of \(N\) or \(R\). Sugar molecules in water are too small to see, even with a microscope, so he had no way to measure them directly. All he had was an equation with two unknowns. To determine the unknown values, he needed another equation with more information about these quantities.
Where could Einstein get more information about the number and size of the particles? Well, he knew he could imagine the sugar as a huge number of independent molecules jiggling about, i.e. the the atomic hypothesis. And that's exactly what Einstein did. In particular, he inferred from the microscopic-macroscopic connection that the sugar molecules should obey the ideal gas law, \(PV = NkT\). This equation contains explicit information about the number of molecules \(N\), and in particular how they are related to pressure, volume and temperature.
Einstein then just balanced two effects. The first effect is the force of gravity pulling the particles down, which tends to make them bunch up near the bottom of their container. The second effect is the force of the thermal scattering of sugar molecules around the liquid. What does this mean? Remember above that we said that when molecules are more dense, there is greater pressure. This is a consequence of the ideal gas law. And why does the system obey the ideal gas law? Because Einstein assumed that it is described by atoms following a random walk. So, as gravity pulls the molecules down, there is a pressure that develops in the opposite direction, which pushes to the molecules to diffuse back up again. The latter is just another way of describing the diffusion process introduced above above. The two effects are pictured in the images below.
The effect of gravity (left) and diffusion (right) on the particles in sugar water. Image Credit: John D. Norton
Combining the effects of gravity and of diffusion allowed Einstein to determine a new relationship between the number of molecules and the radius. The main observation was that equilibrium occurs when these two effects balance and are equal. Setting these effects to be equal turns out to provide another expression involving the number and radius of the molecules, \(N = d\times 1/R\), where \(d\) is just a constant that incorporates the rate of diffusion, which Einstein could also measure. He now had two equations and two unknowns:
- Viscosity Analysis: \(N = c\times 1/R^3\)
- Atomic Analysis: \(N = d\times 1/R\)
Combining these two equations finally allowed Einstein to calculate the exact values of \(N\) and \(R\), in terms of the measurable quantities \(c,d\) whose values were known.
Don't worry about trying to memorise the details of Einstein's calculation, which was notoriously difficult (although you are welcome to read about it in his dissertation for yourself). Just remember the important part: by proposing to think of dissolving sugar in terms of its molecules jiggling about along random walks, Einstein was able to use some clever reasoning to calculate the number and size of these molecules.
Application 2: Einstein's Brownian motion paper
The reasoning above turned on this interesting fact, that molecules collecting in one region of a vessel gives rise to a pressure difference, which actually pushes the molecules away from that region. Let's think about this idea a little more.
Challenge Question. When you have a helium balloon inside a closed car, what direction will the balloon move in when the car accelerates forward? What direction will it move in when you slam on the brakes? Take a moment and think about it. Then have a look at the answer in the video below (you can find many versions of this same experiment on Youtube).
Why does the balloon behave this way? It is because of a pressure gradient. When the car accelerates forward, the molecules of air get flung towards the back of the car. But remember our reasoning above: greater density means greater pressure. So, when you accelerate forward, there is actually higher air pressure toward the back of the car than in the front. This pressure gradient causes the balloon to get pushed forward.
Einstein used exactly this reasoning in his doctoral dissertation. And he used this same reasoning in his analysis of Brownian motion.
Recall the big difficulty of Einstein's dissertation: the sugar molecules were too small to be able to directly measure their radius, so he had no way to determine the number of molecules. But what what if they weren't? What if we had a liquid with much larger molecules suspended in, like pollen grains or fat globules? Then we would know the radius of the molecules, and so there would only have one unknown, \(N\), and Einstein's analysis would determine it.
Is this how Einstein's thinking went? Einstein didn't say, so we'll never know for sure. But as Einstein historian John D. Norton points out, this reasoning would have been obvious and direct given what he did in his dissertation.
All the reasoning needed for Einstein's argument in this paper has now already been done: just suppose that the visible pollen or fat molecules suspended in water are enormous in number, and jiggling in random, mutually independent motion. Then Einstein's same calculation from his dissertation establishes, by balancing the effect of gravity with diffusion via a random walk, that,
\[ N = d\times 1/R, \]where again \(d\) could be determined by measuring the rate of diffusion of the molecules, and \(R\) could be measured as the visible radius of the suspended molecules. So, this equation now gave Einstein a direct way to determine the value of \(N\).
After doing this calculation, Einstein proposed for the first time that the collision of water molecules with suspended pollen would give rise to a visible jiggling. This led him to his famous comment that this might very well be the jiggling that had been observed by Brown in 1827. When studying Pinkfairy flowers from the Pacific Northwest of the United States (called Clarkia pulchella after the explorer William Clark), Brown noticed that the pollen grains discharged tiny pollinating particles that exhibited an apparently random "jiggling" motion in water, which no one had been able to explain for decades. For particles of size 0.001mm, Einstein predicted a displacement of 6 microns per minute. This prediction was soon confirmed by experiment, which provided good evidence that Einstein's analysis was correct.

Clarkia pulchella (left) and its pollen grains under an ordinary microscope (right inset image) and an electron microscope. Microscope image credit: Pearle et al.
The significance of this discovery was enormous: Einstein had discovered a visible phenomenon that required atoms in order to understand it. He had assumed that atoms exist, and that their bulk behaviour can be described by a random walk, which give rise to a pressure from diffusion. Once the experiments were in, and Einstein's prediction turned out to be correct, his analysis provided some of the most compelling evidence ever that the world is made of atoms. This answered a long-standing question in the foundations of thermal physics: do we need the atomic hypothesis in order to accurately describe the world? After Einstein's work, this necessity was hardly up for debate. Atoms were here to stay.
