The lecture traces through some important episodes in the discovery of quantum theory (sometimes called "Old Quantum theory"), and makes three main points:
- Discrete energy. Thinking of light in terms of discrete particles or "energy packets" in random motion helped Planck and Einstein explain two long-standing puzzles (black-body radiation and the photoelectric effect), and gave rise to the Planck-Einstein energy equation, \(E = hf\).
- Waves-Particle duality. It is possible to think of all matter in a similar way: particle-like packets whose statistical behaviour gives rise to wave-like phenomena; thinking in this way gives rise to the De Broglie momentum equation, \(p = h/\lambda\).
- The Bohr Atom. These ideas allow a natural account of the structure of atoms, which avoids the problems of previous account, and also explains the origin of colour.
These "Extras" will provide some more detailed information about a few topics appearing in the main Lecture 3 reading.
What makes something a wave?
Periodic Motion
A classic example of periodic motion is an ocean wave. It may look like an ocean wave is a giant object that comes crashing towards you. But its origin is really in the periodic up-and-down motion of the molecules of water, illustrated in the image below.
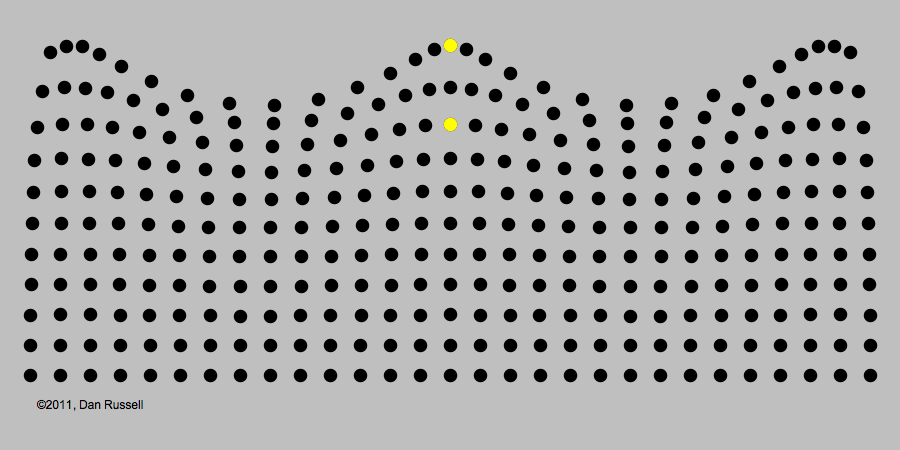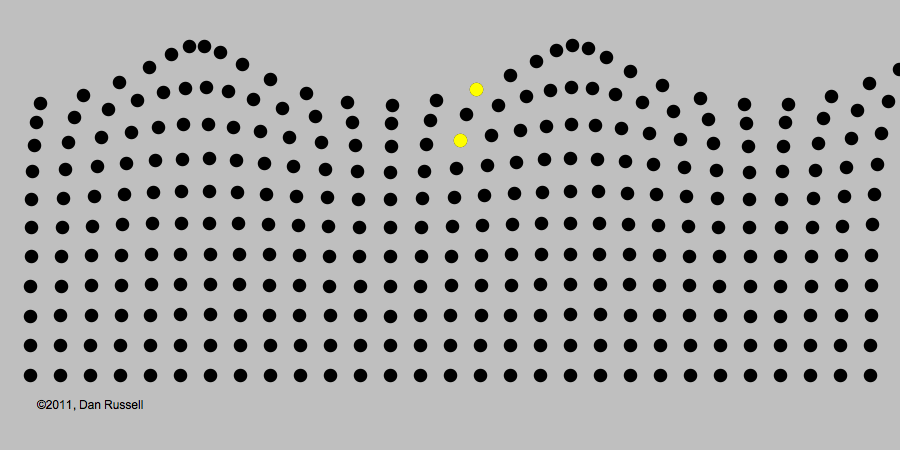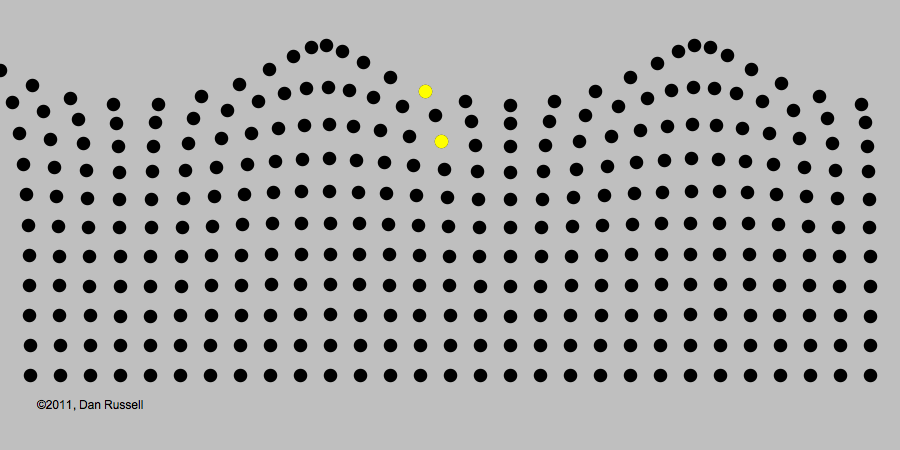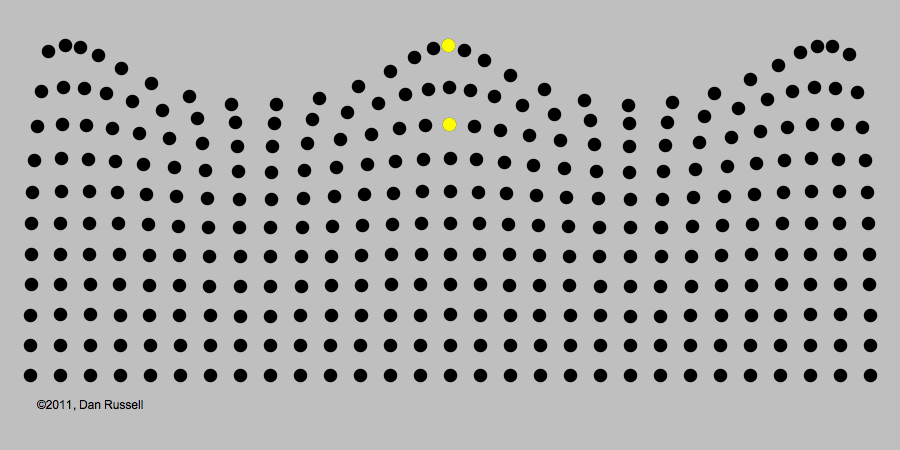
Like all waves, light can be described in terms of periodic changes, which are in some ways analogous to changes in a water wave. The major difference, as we will see, is that there is no underlying medium analogous to the water for the wave to travel through. Although 19th century electromagnetism postulated the existence of such a medium (called the "luminiferous aether," extensive experiments found no evidence of it. The lack of this medium became an important piece of evidence that a radically revised theory of light would be needed.
Diffraction
Waves also undergo diffraction when they pass through an appropriately-sized hole. Diffraction describes the bending of a wave around corners. For example, when a wave hits an obstacle like a wall with a slit in it, the wave continues on the other side in a circular shape as expanding out away from the slit.

Like all waves, light will diffract when shined through a very small hole.
Interference
Thomas Young studied interference in London in 1801, finding that when two waves meet each other, the waves combine interesting ways.


Two crests combine and form a larger crest, while troughs combine to form a larger trough. This is called constructive interference. But when a wave crest combines with a wave trough, they cancel each other out and the wave disappears. This is called destructive interference. You can see this in action in the image below. The first two waves are transmitted at different speeds, and the third, bottom wave is the combined effect of both interfering.
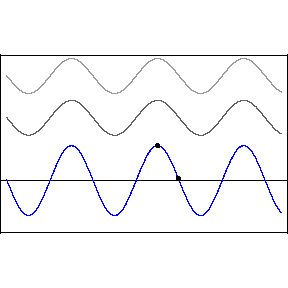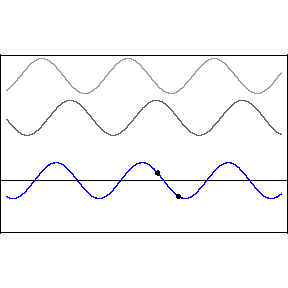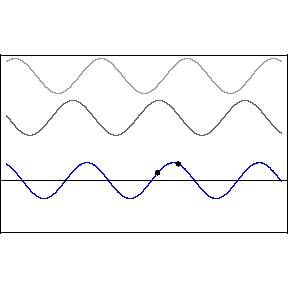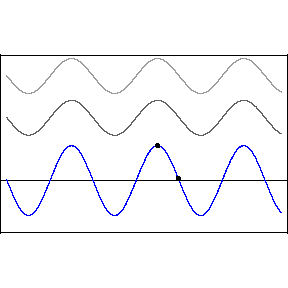
Like all waves, light can be made to interfere by shining it at a pair of very small holes or "slits" in a barrier. The two waves that result on the other side combine to form a pattern of construction and destruction. With light, we find that this gives rise to changes in the brightness of the light, with constructive and destructive interference giving rise to a pattern of light and dark stripes on a screen set up in front of the two slits.

This pattern is a signature of phenomena that are waves. When light was found to behave in this way, it was quickly accepted as a wave.
More about the photoelectric effect
What we see
Hertz and Hallwachs discovered in 1887 that if you shine light at a metal plate, the light smashing into it can knock electrons out of the plate. They were actually able to see a spark when this happened. Today, we can measure the effect with a voltage meter.
First, whether or not electrons are ejected depended on the colour of the light. The effect does not occur at all with red light. But blue and ultraviolet light gave rise to a large effect, with many electrons being ejected.
Second, increasing the intensity of red light does nothing to make the effect occur. For example, you could move the light source very close to the plate, which means that more of each wave crest strikes the plate and thus has greater intensity, and the effect still will not occur: not electrons will be ejected.
Radiation pressure
The structure of light is microscopic, whereas the visible properties of light like frequency and intensity are macroscopic. The photoelectric suggested that physicists didn't yet fully understand the microscopic nature of light. What was needed was a way to infer the microscopic from the macroscopic.
Einstein's old trick, discussed in Lecture 2, was to connect the ideal gas law \(PV = NkT\) with a system of independent particles following a random walk. So, if we could show that light obeys the ideal gas law in an appropriate way, then perhaps we could use this to infer that light behaves like particles.
It turns out that there is an analogue of the ideal gas law for light, which is associated with radiation pressure. This pressure from light is the reason that a comet's tail always points away from the sun: the higher quantity of light near the sun gives rise to a difference in pressure, which pushes the tail of the comet away.

In particular, it turns out that light satisfies an ideal gas law of the form \(P = (N/V)kT\), where the particle number \(N\) refers to a number of "particles" of light, sometimes called photons.
Optional: More on Radiation as an Ideal Gas
Einstein and the Diffusion of Light
Just like pressure, it is possible to measure the diffusion of light radiation macroscopically, for a given frequency of light. And just like with pressure, one might try to seek a microscopic description of the same phenomenon in terms of microscopic random particles.
This was Einstein's brilliant idea: describe light in terms of a jumble of discrete particles called "photons" undergoing a random walk in their container.
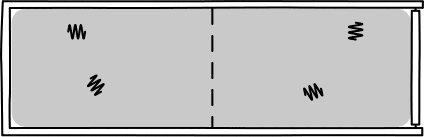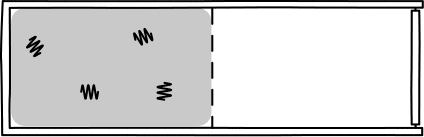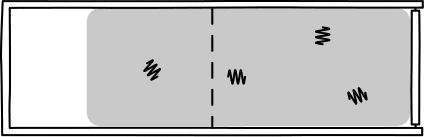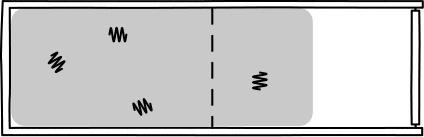
Image Credit: John D. Norton
This picture allowed Einstein to infer that, assuming a particle of light is equally likely "randomly walk" into each side of a box, then the probability of appearing in one half is 1/2. So, since the particles are assumed to be independent, \(n\) particles would be found in one half of the box with probability \((1/2)^n\). Such probabilities allow one to calculate the rate of diffusion for light radiation in a container.
However, the diffusion of light radiation is macroscopic, and had already been measured. So, Einstein set his calculated rate of diffusion to that number, and then worked backwards to calculate the number of particles \(n\). What he found, remarkably, was that the number of "particles of light" \(n\) was closely related to Planck's equation. In particular, it was given by,
\[ n = E/hf, \]where \(E\) is the energy of the radiation, \(f\) is the frequency, and \(h\) is Planck's constant.
In summary, Einstein had used macroscopic knowledge about the entropy of light to infer that its microscopic composition might be expressed in terms of particles. This finally sense of the photoelectric effect. Why doesn't the quantity of light matter for determining whether or not electrons will be ejected from the plate? Because, if your particles have low energy, then it doesn't matter how many of them smash into the plate — each individual particle lacks the energy to eject an electron, and so putting more of them to the task won't help. On the other hand, if you give a particle greater energy (and blue and ultraviolet light have greater energy), then you will see more particles ejected.
Thus, Einstein suggested in a very careful and hesitant remark, his analysis of light might finally solve the puzzle of the photoelectric effect. He wrote:
"Monochromatic radiation of low density behaves — as long as Wien's radiation formula is valid — in a thermodynamic sense, as if it consisted of mutually independent energy quanta of magnitude [hf]."
Einstein carefully hedged his statement because he knew that it may well imply a revolution: the quantum revolution.