Having an effect on the past
We know that because of the grandfather paradox, it is impossible to go back in time and kill your grandfather. However, it may still be possible to have an effect on the past. Consider the following sequences of events.
- You have a limp.
- You go back in time and shoot your younger healthy self in the leg.
- Being shot in the leg, you develop a permanent limp.
- Return to top. ↵
This chain of events is perfectly consistent. Indeed, it is a situation in which you must go back and have some effect on your past self, since otherwise there would be no explanation of your limp. Another such case is the following.
- Your grandfather teaches you how to build a time machine.
- You ask, "Who taught you?" and he replies, "You did!"
- You build a time machine on his instructions.
- Using the time machine, you go back to when your grandfather was a boy.
- You teach your young grandfather how to build a time machine.
- He asks, "Who taught you?" and you reply, "You did!"
- Return to top. ↵
This is another case in which you have no choice — you must go back in time. For otherwise, there would be no explanation of how your grandfather learned to make a time machine. Of course, you might well ask, "where did this information come from in the first place?" There appears to be no obvious answer. There is simply no fact about its origin.
This may seem intuitively absurd. How can a phenomenon lack an explanation? How can an effect lack a cause? However, it is important to think about where our offended intuitions come from. Our everday intuitions about 'explanations' and 'causation' are drawn from experiences in which time travel does not occur. So, there is no guarantee that Nature will continue to respect our intuitions when time travel occurs. Like many things, causation and explanation are exeedingly strange in time travel universes. Today, we're going to explore a sense in which such happenings are licensed by our best theory of space and time.
We have an incredibly successful theory for discussing the nature of space and time, which is Einstein's theory of relativity. So, it is only sensible that we should look to our best scientific theory for advice about the status of time travel.
Is time travel possible in modern physics, for bodies that move slower than the speed of light? To answer this, we'll need to say more about what me mean by time travel. Many philosophical discussions of time travel like that of David Lewis are not precise enough to even answer this question. Fortunately, we can use the tools of relativity theory to make progress on the question.

Image: John D. Norton
Relativity and time travel


The analogy to think of here is pieces of a puzzle. If each piece provides a description of a possible region of space and time, then by fitting the pieces together smoothly we get another possible description of space and time.
This fact has some very interesting consequences as far as what's possible. All that's needed to see this is a little creativity. For example, suppose I were to draw a circle on the wall and identify it with a circle on a different wall. "Identify" means we consider the points of the two circles to be identical, corresponding to a single region of spacetime. What happens when I push my hand through the circle in wall? It will come out of the circle in the other wall. That is a perfectly possible spacetime from the perspective of relativity theory.
Another interesting fact is that pacman spacetimes are possible. That is, it is possible for spacetime to look like a sheet of paper that is rolled up along the spatial access, so that if you walk long enough to the right, you will eventually come out on the left (as Pacman does when he leaves the edge of the screen). Such a world is called spatially closed. Interestingly, this very idea was proposed as a model of our Universe by Einstein himself; it is now known as "the Einstein Universe."

Image: John D. Norton
Now, let's go back to time travel. What's the easiest way we could possible create a time travel universe? Just take an empty spacetime, described in two dimensions by a sheet of paper, and roll it up along the time axis. For example, recall our spacetime diagram of a man walking up to a tree and back from last time.
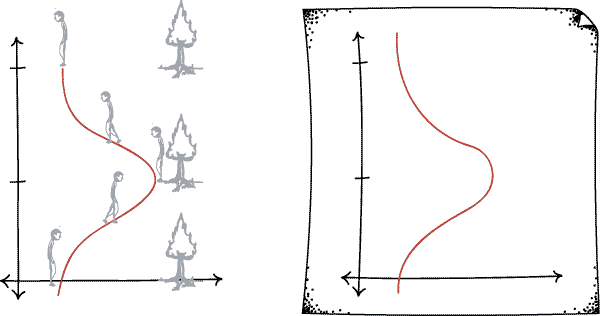
Now just take the sheet of paper and roll it up. As long as everything fits together smoothly, we get another perfectly "possible universe" according to relativity theory.
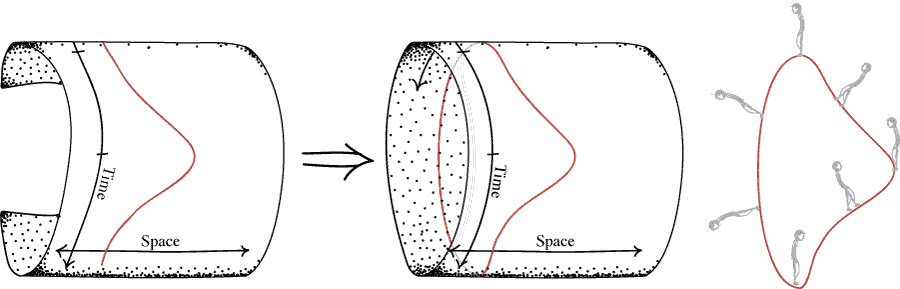
The result is a scenario in which a man repeats the same events over and over again, similar to the movie Groundhog's day with Bill Murray. The resulting curve is referred to as a closed timelike curve.
Closed timelike curves satisfy a certain definition of time travel that has been suggested by Frank Arntzenius. Draw a little region R on any such time travel spacetime, say in the shape of a square. Inside the region R, an observer will experience A first and then B, no matter which worldline that observer travels on. Let us say that 'time travel occurs' if and only if in spite of this, the spacetime as a whole includes a segment of a worldline on which the order of A and B is reversed. This is possible in our rolled-up spacetime: for an observer that begines at B and goes around the loop, it is possible to experience first B and then A.
Consistent interaction with the past
The Grandfather Paradox prevents you from killing his grandfather before he meets his grandmother. But we saw in the beginning that it is perfectly possible to maim him, teach him how to build a time machine, or any number of other things. That is, it is perfectly possible for you to interact with your grandfather (or yourself, or whoever), as long as you do so in a way that is consistent.
Is it possible to consistently interact with your past in relativistic spacetimes with closed timelike curves? The answer is yes. As an example, let's see a sense in which it is possible for a particle to collide with its past self.
To begin, consider how a collision between two billiard balls looks in an ordinary spacetime.

Image: John D. Norton
Ball A is moving to the right and collides with Ball B, which was previously at rest. This causes Ball A to come to rest, and Ball B to start moving to the right.
Now go back to the simple time travel spacetime introduced above. Without too much effort, it is possible to arrange the collision so that two billiard balls are actually earlier and later versions of one and the same billiard ball. In other words, the billiard ball is able to collide with itself.
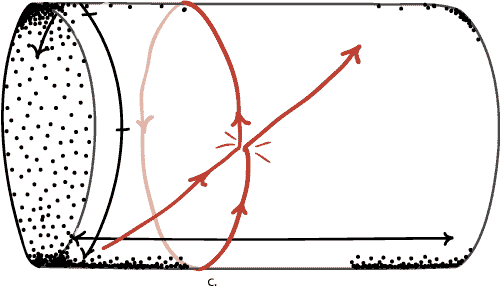
Notice that "cause and effect" has a strange circular character in such universes. The past version of the ball causes the future version to start moving, and the future version causes the past version to stop. Does the past causally effect the future, or does the future causally effect the past? The answer here seems to be "both." This is strange indeed. But we have already seen that explanations can also also have this circular character in time travel universes, so perhaps it isn't so surprising that causation should be circular as well. We never said that time travel wouldn't be strange!
The ideality of time
One of the first time-travel spacetimes discovered in relativity theory was Gödel spacetime, discovered by the logician Kurt Gödel. In addition to having closed timelike curves, Gödel spacetime turns out to admit another strange feature with respect to time: in this spacetime, it is impossible to define the passage of time in any global sense.
Discussions of time in relativity theory often presuppose that it is possible to define a 'universal moment in time', which consists in all the things that are happening throughout the universe at that moment. Such a moment is referred to as a hypersurface of simultaneity. It is a 'slice' of 3-dimensional space at a time. And until Gödel spacetime was discovered, it was assumed that such a 'slice' always exists.
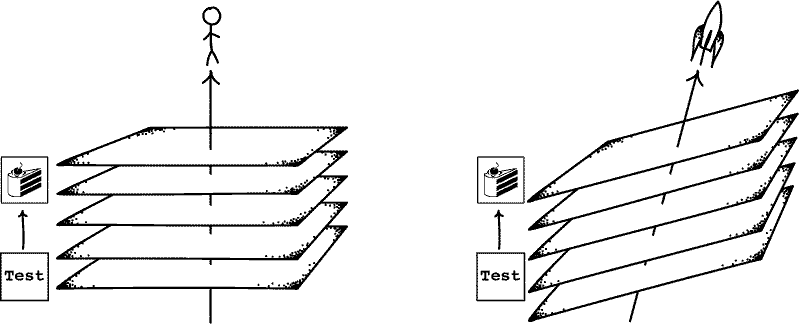
However, the logician Kurt Gödel showed that there is a possible spacetime in relativity theory, known as Gödel spacetime, in which no such hypersurface exists. In Gödel spacetime, a global 'moment in time' isn't just ambiguous; it does not have any meaning whatsoever. Although in a small region of Gödel spacetime it is always possible to find a spatial slice, it turns out that there does not generally exist one that spans all of space at once.
This led Gödel to suppose that time is not real, since a 'moment of time' does not make sense. Gödel saw this claim as in the spirit of some British and German idealists, who claimed earlier in the 20th century that time is not real. His argument (which you can read for yourself here) had two parts:
(1) Gödel thought that our own spacetime might have this same property of Gödel spacetime, in which ase 'a moment in time' could not be defined; and
(2) He thought that even if that were not the case, the fact that there is a possible spacetime with this property is enough to be suspicious that time is not real.
Gödel's argument has been criticised as not a conclusive argument for the unreality of time. However, I leave it to you to decide how plausible it is.
Are time travel universes plausible?
Time travel universes allow for a number of strange phenomena: circular causation, circular explanations, and spacetimes in which a 'moment of time' is not defined. Do all these strange features amount to an argument against time travel?
The argument against time travel would run as follows. As a matter of empirical fact, we do not experience visiting time travelers, billiard balls self-colliding, circular causation, circular explanations, etc. By induction from our repeated experience, it one might conclude that these effects are very implausible. So, since time travel requires many such effects, it follows that time travel is implausible.
Is this a good argument? Well, philosophers and physicists go back and forth about this. There are lots of things we don't experience, such as the center of a black hole, and yet most physicists believe that black holes (and their fearful centers) do exist. Perhaps time travel is like that, and we might still some day find reason to believe that it might happen somewhere in the universe.
Relativity theory certainly allows for time travel in an important sense, just as it allows for black holes. But one might respond that this is a problem with relativity theory, and which reminds us that we must continue the search for a better theory of space and time. It is far from clear whether this philosophical attitude is the correct one to have.
Let's conclude with a brief comment on Lewis' question of whether or not you "can" kill your grandfather in some sense. That is, enough of the huff and puff, can you kill your grandfather as a young man or not? There is a gigantic debate among a certain style of philosopher of a certain stripe about this question. Here, let us simply observe that this question is totally irrelevant to the question of whether or not time travel is possible. Time travel is an empirical question about the way our universe is. Debating the different linguistic senses in which you "can" and "cannot" kill your grandfather in such universes is irrelevant to the question of whether or not time travel is possible.