Zeno Paradox 1: Achilles and the Tortoise
Achilles is a lightening fast runner, while the tortoise is very slow. And yet, when the tortoise gets a head start, it seems Achilles can never overtake the tortoise in a race. For Achilles will first have to run to the tortoise's starting point; meanwhile, the tortoise will have moved ahead. So Achilles must run to the tortoise's new location; meanwhile the tortoise will have moved ahead again. And it seems that Achilles will always be stuck in this situation.

So, it seems Achilles can never overtake the tortoise.
Zeno Paradox 2: The Dichotomy
This version of the paradox says, forget about the tortoise. Achilles can't even make it to the first flag! For in order to do so, he would have to first go half thte distance. Then he would have to go half that distance (or 1/4 of the total). Then half that distance (1/8 of the total). And so on ad infinitum. Since there are infinitely many "halves" for Achilles to cross, he can never make it to the first flag.

This reasoning has an extreme consequence. For just ask whether you can move from one point in space to any other point at all. So, Achilles cannot move at all. Another way to put this is in terms of a regressive version of the problem. Here we imagine what it would look like if Achilles did arrive at the flagpole, and then play his trajectory back in reverse.

In order to reach the flag, Achilles would have to complete the last half of the race. But before he can do that, he must complete the 1/4 of the race just prior. And before that he must complete 1/8 of the race prior, and so on. There is no end to what he must do before completing the race — indeed, it looks like Achilles can never get started in the first place!
Zeno Paradox 3: The Arrow
.png) The "Arrow" version of the paradox argues that an arrow in flight does not move at all.
The "Arrow" version of the paradox argues that an arrow in flight does not move at all.
To begin, we take any given instant. At that instant, the arrow occupies an arrow-sized space. It thus has no room to move. Nor can it since motion takes place over time, and an instant is no duration of time at all. So, the arrow must be motionless at that instant.
By the same argument, it is motionless at every instant, and so it cannot be in motion at all.
Zeno Paradox 4: The Stadium
Zeno's original statement of this version of the paradox is not quite as clever as the previous examples. He starts by considering an arrangement of cars (or rather chariots!) moving back and forth past each other as below.
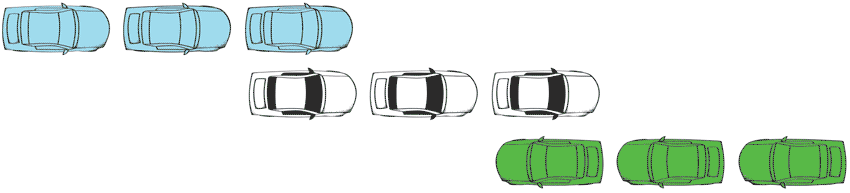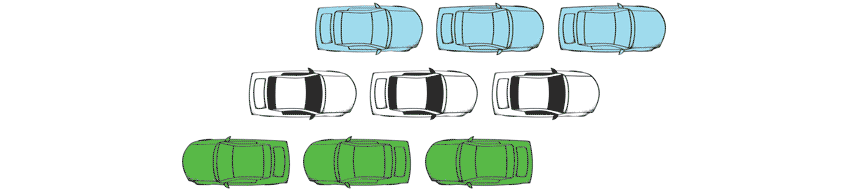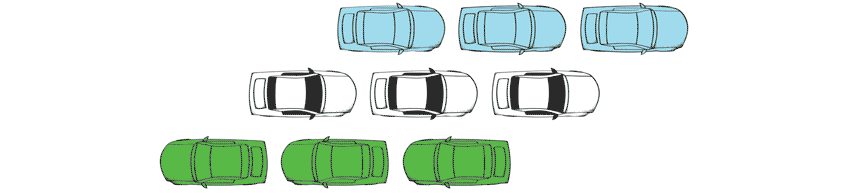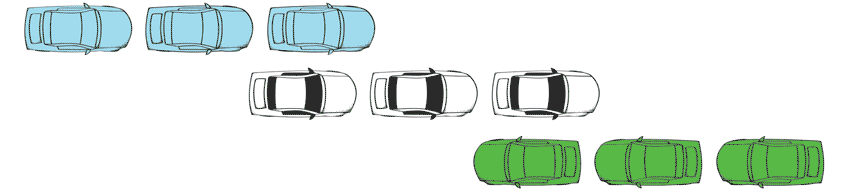
Zeno noticed that if you ask how fast the blue cars are moving, the observers in the white cars and the green cars will disagree. In particular, the green car observers will say the blue cars are moving twice as fast. This is just a simple fact of relative motion. Zeno seems to have found it was problematic.
Salmon has put a spin on this problem that is somewhat more interesting. Many have suggested that space might be discrete, or in basic "chunks," rather than a smooth continuum. If that's right, then the motion of the cars might look something more like this.

Then we notice a strange fact. Focus on the middle blue car. When is it right next to the green car?
The answer is: never! Although the cars appear to move past each other, there is no moment when this passing actually occurs. So, if space is discrete, then it seems motion cannot happen either.
Saving Achilles: Infinite Sums
Introducing the limit of a sequence
The basic solution to the first two versions of Zeno's paradox was the discovery that an infinite sum is a meaningful concept.
We will see that it is not only possible to talk about an infinite sequence of every-increasing lengths, but it is possible to know what just what that sequence is approaching and how that approach happens. In this way, we can explain how Achilles manages to run the race and get to the first flag, overtake the turtle, and generally do whatever godly things he likes to do.
What made this discovery possible was the development of the limit. Intuitively, a limit is what an infinite sequence is forever approaching. But don't be fooled. The limit is one of those absolutely earth-shattering concepts that changed absolutely everything we know about the world, but which many don't realize is quite so important.
Virtually every field you can think of makes use of formal limits, since they are essentially anytime you want to talk about continuity, continuous change and approximation. These concepts are ultimately be grounded in the notion of a limit. I'm sure you can think of a few important phenomena that involve continuous change: the human aging process; a space ship's trajectory; the inflation of currency; the earth's average temperature; etc. These are all things that require a notion of continuous change, as well as approximation techniques.
Not as easy as you'd think
Without a limit, our understanding of all of many important phenomena would fall apart. And yet, it is not so easy to define. The example below illustrates how non-intuitive. Consider the following sequence of shapes.

What limit is the length of the blue line approaching? Is it the the length of the black line? You might think so, since the blue line is getting spatially closer to the black, but this would be wrong. Just think about how long the blue line is in each triangle in the sequence.
The answer is that the blue lines are the same length in every triangle. You should be able to see this by just looking at how each new triangle in the sequence is created by "bending down" the line that makes up the previous triangle. The result is a new shape that preserves the original length of the blue line.
The problem is that this is not the length of the black line. You can see this by "streatching out" the blue line as below, and noting that it is longer than the black. This is also a provable fact about Euclidean geometry that follows from the "triangle inequality."

This is why Salmon says that we didn't understand limits until the 19th century, although people often talked about limits in imprecise terms until that time.
The discovery of the definition of a limit
In the 19th century, this problem was solved when a new concept of a limit was discovered. The definition of that limit is the following. Take any ordered set of numbers, which I'll right,
M1, M2, M3, M4, ...
e.g., 1/2, 1/4, 1/8, 1/16, ...
We say that such a sequence has a limit L if the terms in the sequence can be made to come as close to L as we like as we go higher and higher in the sequencee.
That is the definition that we will work with. It can be made a little bit more precise. You will not be asked to recall this more mathematical version, but it is absolutely worth wrestling with conceptually if you have never done so! That definition is: Say that L is the limit of a sequence M1, M2, M3, M4, ... if for every number ε>0 (the degree of closeness) there is a point in the sequence, say the term S, beyond which every term thereafter is within ε of L.)

So, for example, the limit of the sequence 1/2, 1/4, 1/8, 1/16, ... is zero! No matter how close to zero we want to be, we can always find a point in the sequence beyond which every term thereafter is at least that close. So, we say that the sequence converges to 0 in the infinite limit.
The bottom line is that given an infinite sequence, the limit is a meaningful concept. We don't need to say whether or not it's possible to go all the way to infinity — we can just consider the limit instead. A limit need not always exist, but at least we can speak meaningfully about it.
Infinite Sums and the Achilles Paradoxes
Now we have a way to solve the first two paradoxes.Let's focus on the second paradox, the Paradox of Dichotomy, since the Achilles and the Tortoise Paradox is solved in the same way. The description of the paradox observes that Achilles must travel an infinite sequence of lengths.

However, the fact that Achilles must cross an infinite number of intervals, he does not need to travel an infinite distance. How long he must travel is given by the following sequence:
1/2
1/2 + 1/4
1/2 + 1/4 + 1/8
1/4 + 1/4 + 1/8 + 1/16
:
:
Using the definition of a limit, one can show that this sequence converges to the limit 1. You can find the proof of this fact itself in Salmon's article. And thank goodness! It seems that Achilles does travel the entire distance of the race course after all.
Thus, the first two Zeno paradoxes can be avoided, although the problem required hundreds of years of study and the introduction of an entirely new concept, that of a limit, in order to solve.
Saving the Arrow: Functional Motion and Instantaneous Velocity
The arrow paradox has a solution as well, which similarly involves the development of a better mathematical description.
The problem with the arrow, conceptually, is the problem of defining motion at an instant. We run into difficulties when we try to think of an arrow as "moving during a single moment."
.png)
A simple alternative become available with the modern idea of a function, as ordered pairs of "inputs" and "outputs."
For example, you are familiar with the function,
f(y)=y2.
You can think of this as giving you an output (the "square") for every input (a number.) So, if input the integers, we get in particular the following list of ordered pairs.
(0, 0)
(1, 1)
(2, 4)
(3, 9)
(4, 16)
(5, 25)
:
(y, f(y))
:
The paradox of the arrow is solved once we realize that we can think of motion similarly. Then we have a perfectly good description of the arrows motion, by just inputing a time, and determining where the arrow will be. No other description is needed, and so there is no paradox.
In particular, we can think of position as a function of time, x(t).
For example, if the arrow is traveling with constant velocity, then it will have position given by x(t)=vt. We can even talk about instantaneous velocity in such scenarios using the tools we have developed so far.
Namely, velocity is just the change in distance over time. So, instantaneous velocity is just the limit of average velocity as the interval of distance shrinks to zero. (For the case of the arrow with constant velocity, you can use our definition to show that the instantaneous velocity is just v.)
Saving the Stadium: The Weyl Tiles
The final Zeno paradox, that of the stadium, arose out of assuming space is discrete. So, do we have good reason to reject that assumption?
The physicist Hermann Weyl gave an argument that space is not discrete, which goes as follows.
First, note that there is a certain fact about right triangles that seems to hold, not just mathematically, but as a fact about our world. Namely, take any right triangle like the following.

Then the hypotenuse will be the longest side. In continuous spaces, such as the kind studied by Euclidean geometry, this is a mathematical fact. But it also appears to be a fact about our world, which you can check by just drawing a right triangle and measuring it with a ruler.
What Weyl pointed out is that this fact always fails in a certain kind of discrete space. You can see this by just looking at the discrete analogue of a right triangle, which looks like this.
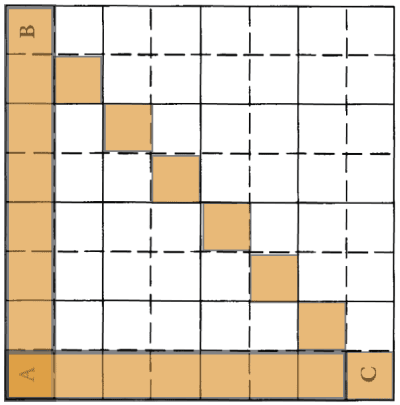
We simply observe that the triangle has the same number of tiles on every side. And this is true no matter how finely we draw the squares, either larger or smaller.
This then may then provide a sense in which our world cannot be discrete, since we appear to measure triangles that have a longer hypotenuse. If the argument works, then we have at least one to resolve the Stadium version of Zeno's paradox, since we reject the assumption that makes it a paradox. However, you might find something questionable about Weyl's argument, and you are invited to investigate this more.
Certainly, we should hesitate to reject this assumption too quickly given the state of modern science, as a quick look at the titles of many recent articles in physics shows that scientists take the possibility of discrete space very seriously. There are many who think that this may be a promising way to develop modern physics.
So, that leaves the question to you, the philosopher: can you think of a good way to avoid the stadium paradox, while still retaining the possibility of discrete space?
A preview: Thomson's Lamp
To conclude, here is a problem that we will deal with next time, but which I would like you to go home and think about this week. Take an ordinary lamp.
Suppose that we switch the lamp off after 1/2 a minute, then on after 1/4 a minute, then off after 1/8 a minute, on after 1/16, and so on ad infinitum. By the same limiting argument used to solve Zeno's paradoxes of Achilles and Dichotomy, we know that this procedure will be complete after a single minute has passed (since 1 is the limit of the infinite sum, 1/2+1/4+1/8+1/16+...).
Question: What will the lamp look like after that minute has passed? In particular, will it be on or off?