Infinite Numbers

The excitement of the infinite

Infinity is a strange and exciting concept.

It has been historically identified with the incomprehensible. Humans are mere finite beings, the idea goes, and so can only comprehend the finite on the best of days. When we try to reason with the infinite, we should expect to become confused by the strange and fantastical things we find.

For example, we have seen in the example of the Hilbert hotel: given a hotel with room for every natural number, it is possible for the hotel to be full, but still admit one more guest: just ask each person to move down one room, from 2 to 3, from 3 to 4, and so on. The result is that everyone still has a room, but one new room is now free.

Hilbert's hotel: An infinite hotel can be full, and still admit one more person.

Philosopher of science John D. Norton pointed out another amusing example. Consider a helicopter floating above the ground. Its rotors have some fixed length and speed. Now imagine doubling the rotor length, and halving the speed. A helicopter with these properties will turn out to have the same lift, and thus still float above the ground in exactly the same way as the original helicopter.

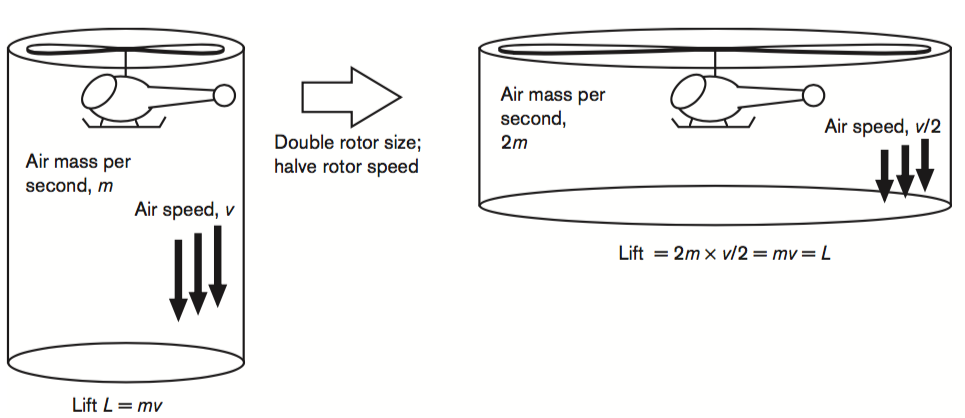
Halve the rotor speed and double the size: the resulting helicopter produces the same lift (image credit: Norton 2004)

Now repeat this procedure ad infinitum, doubling the size and halving the speed of the rotors again and again. At each stage, the helicopter continues to float in exactly the same way as before. What happens in the infinite limit? It would seem to be the following: a helicopter with infinitely long rotors, which are not moving at all, and which still just continues to float above the ground. But that, surely, is impossible... isn't it?

There is a special charm to trying to comprehend the infinite. As Galileo put it,

"[infinite quantities are] incomprehensible to our finite understanding by reason of their largeness.... Yet we see that human reason does not want to abstain from giddying itself about them." (Galileo 1638, The Two New Sciences)

This 'giddying' paid off: the ideas developed in the logical analysis of numbers in the 20th allow us to very much comprehend infinity, or at least certain aspects of the concept.

Infinite numbers

As we saw in our discussion of what numbers are, Hume's principle provides a clever way to say what the 'number' of the set is. For two sets to be equinumerous means that there is a one-one relation between them. We then say that the number of a set is the collection of all sets that are equinumerous with it.

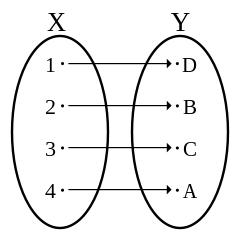
Equinumerous sets stand in a one-one relation.

The 'number' is also sometimes called the cardinality of the set.

Call the number or cardinality of a set finite if it is equal to one of the natural numbers, 0, 1, 2, 3, 4, .... Otherwise, we will say that a set is infinite. Is it possible to talk about the number or cardinality of an infinite set? That is, can we treat infinity like a number?

Sure we can. The concept of equinumerous applies to infinite sets. This is essentially what's going on in Hilbert's hotel. Suppose our hotel rooms are labelled 1, 2, 3, 4, ..., and that so are the original guests: 1, 2, 3, 4,.... Now we add a new guest, which we give the label 0. Are there enough rooms to host everyone?

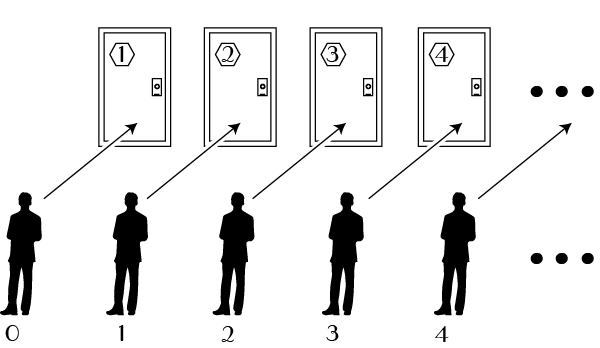
Hilbert's hotel: the one-one correspondence that makes it work

We can see that there are indeed enough rooms by showing that the set of rooms and the set of people are still equinumerous. We do this by establishing a one-one correspondence, for example by showing that is possible the nth person with the (n+1)st room in the diagram above. In rough terms, this establishes the fact that the (infinite) set of positive natural numbers beginning with 1 has the same 'number' or 'cardinality' as the set of non-negative natural numbers starting with 0.

There is a number associated with the set of all natural numbers N = { 1, 2, 3, 4, 5, ... }. The logician who discovered this theory, Georg Cantor, gave it a name: Aleph-nought (pronounced 'AL-if-NOT'). He used the first letter of the Hebrew alphabet (Aleph) with a subscript 0 to represent it, like this:

\(\aleph_0\)

There turns out to be an entire theory of infinite numbers, and indeed infinite numbers of many different sizes. There is an infinite number \(\aleph_1\) that is larger than \(\aleph_0\), and another infinite number \(\aleph_2\) that is larger than that, and so on. This remarkable theory provides a clear sense in which 'infinity' is a number just as much as the natural numbers are. You can study the nature of these infinite numbers in a course on set theory and further logic.

A separate and perhaps more difficult question is whether infinity accurately represents some aspect of the world. Natural numbers can obviously be used to represent various states of affairs in the world. Is it possible to do this with infinite numbers? Our discussion today is an exploration of this question.

The Problem of Supertasks

Two Paradoxes of Zeno

Achilles is a lightening fast runner, while the tortoise is very slow. And yet, when the tortoise gets a head start, it seems Achilles can never overtake the tortoise in a race. For Achilles will first have to run to the tortoise's starting point; meanwhile, the tortoise will have moved ahead. So Achilles must run to the tortoise's new location; meanwhile the tortoise will have moved ahead again. And it seems that Achilles will always be stuck in this situation.

Achilles and the Tortoise: How can a fast runner ever catch up with a turtle without travelling an infinite number of distances?

This is one of a collection of problems known as Zeno's paradoxes. Another version of the problem says: forget about the tortoise. Achilles can't even make it to the first flag! For in order to do so, he would have to first go half the distance. Then he would have to go half that distance (or 1/4 of the total). Then half that distance (1/8 of the total). And so on ad infinitum. Since there are infinitely many "halves" for Achilles to cross, he can never make it to the first flag.

Achilles alone: How can he move it all without travelling an infinite number of distances?

There is nothing special about the particular distance that Achilles is described to have travel here. The same problem holds of any distance at all. This led Zeno to conclude that motion of any kind is impossible. This, it would seem, is a problem.

Thomson's sharpening

Cambridge philosopher James F. Thomson expressed Zeno's paradox as an argument in the following way.

"To complete any journey you must complete an infinite number of journeys. For to arrive from A to B you must first go from A to A', the mid-point of A and B, and thence to A'', the mid-point of A' and B, and so on. But it is logically absurd that someone should have completed all of an infinite number of journeys, just as it is logically absurd that someone should have completed all of an infinite number of tasks. Therefore it is absurd to suppose that anyone has ever completed any journey." (Thomson 1954, pg.1)

Thomson proposes that we think of this passage as an argument:

This argument, it seems, has a wrong conclusion. This only happens when one or more of the following is the case:

• The first premise is false: it is not required that you complete an infinite number of journeys; or
• The second premise is false: it is not impossible to complete an infinite number of journeys; or
• The argument is invalid: the argument is not truth-preserving from the premises to the conclusion.

Thomson, surprisingly, claims that there is a sense in which both the first and second premises are true. To explain this, he takes the third option, and finds the argument is invalid. This is a surprising response because, on the surface, the argument does seem to have the (valid) argument form of modus tollens:

1. (Premise): A → B
2. (Premise): ¬B
3. (Conclusion): ¬A

But this is not how Thomson views the structure of the argument. The only way that the first and second premises are true, Thomson proposes, is that there is a different meaning for proposition B = "you complete an infinite number of journeys" in each of the two cases. That is, we ought to view the structure of the argument as follows:

1. (Premise): A → B
2. (Premise): ¬B'
3. (Conclusion): ¬A

where B and B' are not the same. This argument is indeed invalid: the premises can be true while the conclusion is false.

Thomson thinks that the meaning of the word 'complete' differs in each of the two cases. When we say that a journey 'completes' an infinite number of sub-journeys in Premise 1, we mean that a journey 'consists in' a certain number of sub-journeys. For example, if I ask how to cut up a pie, there seems to be an infinite number of ways to do it. And indeed, I could imagine the pie being composed of infinitely many parts, consisting in ever-smaller slices. This is just a fact about the composition of the pie.

There seem to be infinitely many ways to slice up a pie.

Thomson thinks of the first premise of the Zeno problem, that a journey "completes" an infinite number of sub-journeys, in the same way as the pie. There is of course an infinite number of pieces that I can slice the journey into.

But when we say that it is 'impossible to complete' an infinite number of journeys in Premise 2, we mean that it is impossible to carry out a certain kind of activity called a supertask.

Let's get a little clearer on what Thomson has in mind.

Supertasks

What is a supertask?

Thomson proposes the following definition of a supertask:

"Let us say, for brevity, that a man who has completed all of an infinite number of tasks (of some given kind) has completed a super-task" (Thomson 1954, pg.2)

A supertask is an infinite sequence of activities, each carried out one after the other, and which can each be said to have been carried out in a finite amount of time. How could one possible carry out an infinite number of things in a finite amount of time? There are various ways, which you can find discussed more broadly on the Stanford Encyclopedia Article on Supertasks. But one particularly common way is to say that you carry out a task with increasing speed.

For example, Bertrand Russell proposed the following general strategy. Suppose you have an infinite To-Do List. Being an extremely efficient worker, you decide to carry out the task with increasing speed, in the following way.

An infinite To-Do List

• First task: 1/2 minute
• Second task: 1/4 minute
• Third task: 1/8 minute
• :
• Nth task: (1/2)^N minute

How long would it take you to complete the entire infinite list? The answer is: one minute. You can see this by imagining your allotted time on a timeline. When you line up all the times one after the other, you find that they all fit into a time interval equal to 1 minute. This timeline (below) looks just like the distances that Achilles traverses, and for a reason: those distances sum to 1 in the same sense; and, if Achilles is travelling with the same speed at each moment, then the time required to traverse each interval is described by the very same timeline.

Supertask timeline: time goes from left to right. Each red rectangle represents the time allotted for a task.

There is also a more precise sense in which these durations all sum to one. Consider the sequence that describes how much time has passed as you complete your tasks.

• \(t_1 = 1 + \tfrac{1}{2}\)
• \(t_2 = 1 + \tfrac{1}{2} + \tfrac{1}{4}\)
• \(t_3 = 1 + \tfrac{1}{2} + \tfrac{1}{4} + \tfrac{1}{8}\)
• \(\vdots\)

The limit of this sequence \(t_N\), as we let \(N\) grows without bound, is equal to 1. Here, the 'limit' is a precise mathematical concept, which roughly means: however close you want to be to 1, there is \(t_N\) in the sequence that is at least that close.

The Thomson Lamp

We can write down descriptions of supertasks using the language above. If we're creative, we might even be able to imagine carrying out a supertasks. But is it possible to carry out a supertask? When you ask this question, you should be very careful to also ask what exactly we mean by 'possible'. As you will recall from our discussion of the Kalam cosmological argument, there are various modalities or things that one might mean by 'possible'. For example, one might ask if a supertask is 'logically possible'. Or, one can ask if it is 'physically possible' according to some law of nature.

Max Black argued that supertasks are impossible to complete in a certain logical sense, which can be known even without knowing what the laws of Nature are. In particular, Black argues that completion requires a last task. Since the supertasks described above have no last task, they are all impossible. But why would we say that completion requires a last step? Black gave no serious argument on this point; and, it is not obvious that one should believe him, given that we have described an explicit procedure for completing a supertask.

Achilles does not complete a last step.

For Thomson: supertasks are impossible, but for a different reason. He also they are a logical impossibility. His famous argument for this claim makes use of a thought-experiment now known as 'Thomson's lamp.' Suppose that we turn a lamp on on after a 1/2 minute, and then off after a 1/4 minute, and then on again after 1/8 minute, and so on ad infinitum. What is the state of the lamp if we carry out this task an infinite number of times?

The Thomson Lamp

Thomson's response to this strange question is the following.

It seems impossible to answer this question. It cannot be on, because I did not ever turn it on without at once turning it off. It cannot be off, because I did in the first place turn it on, and thereafter I never turned it off without at once turning it on. But the lamp must be either on or off. This is a contradiction.

The only thing that Thomson finds wrong with this description is the assumption that it is possible to complete a supertask. Thus, he rejects that assumption, and concludes: supertasks are impossible. We can put this another way by using 0 to represent 'off', and using 1 to represent 'on'. Then the sequence of lamp states is described as follows:

1, 0, 1, 0, 1, 0, 1, ...

This sequence does not have a limit: it is not getting arbitrarily close to any single number. So, it is worse than impossible, but actually meaningless to say that the lamp well end in the state described by the limit of Thomson's procedure.

One response could be to redefine what the limit means. For example, mathematicians sometimes make use of another notion of a limit of a sequence (x_1, x_2, x_3,...), which is known as the Cesàro mean. On this definition, we consider the limit of the sequence \(C_1 = x_1\), \(C_2 = (x_1 + x_2)/2\), \(C_3 = (x_1 + x_2 + x_3)/3\), and so on. These numbers describe the average value of the sequence up to a given term. One says that a sequence Cesàro converges to a number C if and only if the Cesàro mean converges (in the ordinary sense) to C. It is then well-known that the sequence \(0, 1, 0, 1, \ldots\) Cesàro converges to ½.

Thomson pointed out that this argument is not very helpful without an interpretation of what lamp-state is represented by 1/2. We want to know if the lamp is on or off! And saying that its end state is associated with a convergent arithmetic mean of ½ does little to answer the question.

The Benacerraf Response

Benacerraf (1962) responded to Thomson's argument by pointing out a sense in which his description is just incomplete. Thomson has described the state of the lamp at every moment before 1 minute has elapsed. But he has said nothing about what happens at 1 minute. This suggests that the description is consistent with either scenario: an 'on' lamp or an 'off' lamp — which one is the case depends on the details of how we carry out the procedure!

Norton and Earman (1996) have made this response precise by describing an actual, mechanical implementation of something like the Thomson lamp.

Suppose a metal ball bounces on a conductive plate and makes a connection that turns on the lamp when it does so. This ball can be set up so that as it bounces, the time between bounces occurs exactly as is needed to complete a supertasks: the first bounce takes 1/2 a second, the second bounce 1/4 a second, and so on ad infinitum. When we take this sequence of bounces together, we get a supertask. The whole scenario is completed in one minute.

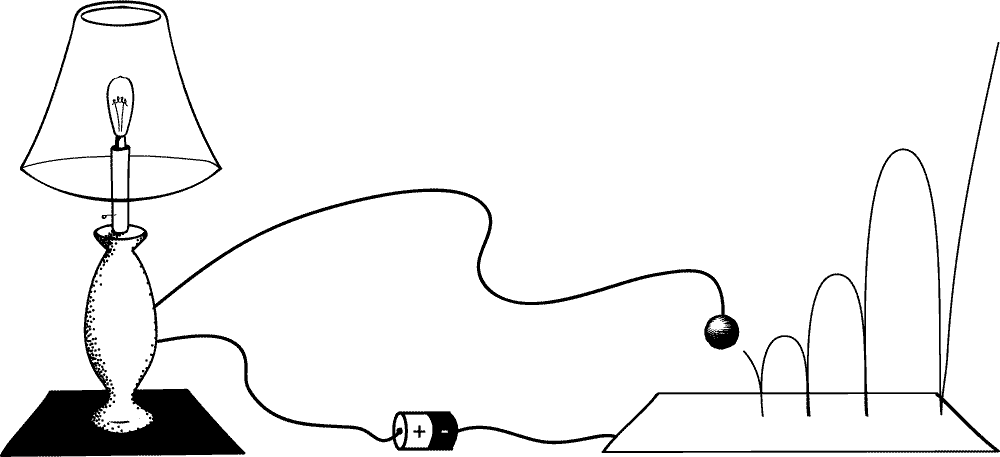
An implementation of the Thomson lamp that ends in the 'on' state

What will happen to the lamp after 1 minute has passed? The ball will be sitting on the plate, and so the lamp will be on!

Another arrangement is to setup a scenario in which the ball disconnects the lamp each time it lands on the plate. A similar supertask then ensues, with the ball bouncing an infinite number of times before finally coming to a rest on the plate, as below.

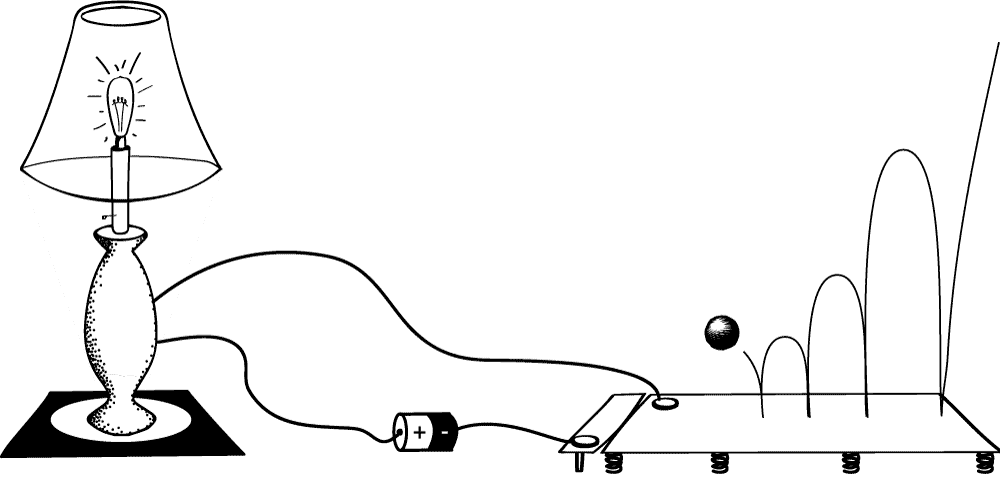
An implementation of the Thomson lamp that ends in the 'off' state

In this case, the ball will end on the plate and disconnect the lamp after one minute. So, on this description, after one minute the lamp will be off.

The Wider World of Supertasks

There is a wider world of supertasks that have been considered, sometimes as part of an argument that supertasks are impossible in some sense, and sometimes just for the fun of trying to better understand the nature of infinity. Here is one to conclude with.

The Ross-Littlewood paradox begins with a jar, and an infinite set of balls, each numbered with natural numbers 1, 2, 3, 4, .... We then design a supertask as follows. In the first step, we place the first 10 balls into the jar, and then remove ball 1. In the second step, we place the second 10 balls in the jar (i.e. balls 11-20), and then remove ball 2. We then proceed like this ad infinitum. We carry out this task with increasing speed, as above, so that the entire procedure is completed after 1 minute.

The question is, what is the state of the jar after the supertask is complete?

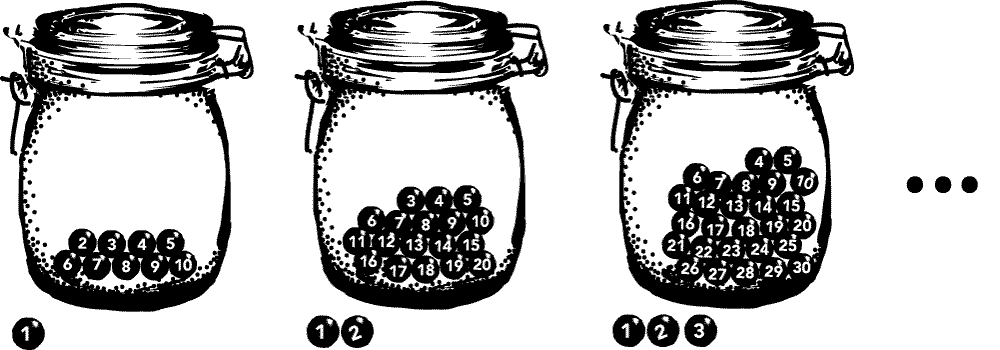
The Ross-Littlewood Paradox

At first blush, the answer seems to be: 'infinitely many'. After all, the number of balls in the jar is dramatically increasing at each step. But it turns out that this cannot be the case. For consider what happens to any individual ball over the course of the supertask. Ball 1 is removed at the first stage. Ball 2 is removed at the second stage. And for any ball you want, say the Nth ball, there is a stage (the Nth stage) at which it is removed.

So, the conclusion seems to be that, after the supertask is complete, there are no balls in the jar! Does this imply that the supertask is impossible? Does it imply that supertasks in general are impossible? Answering such question requires careful analysis not only of the nature of the infinite, but also of what we mean by 'possible'. For now, I leave this (possibly super-) task to you.